线段树

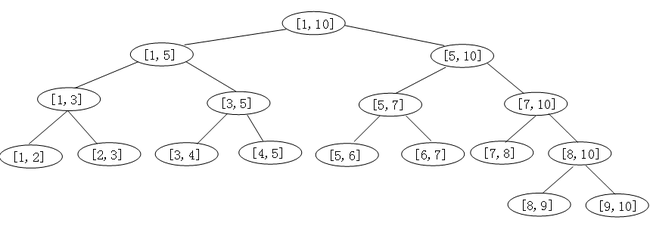
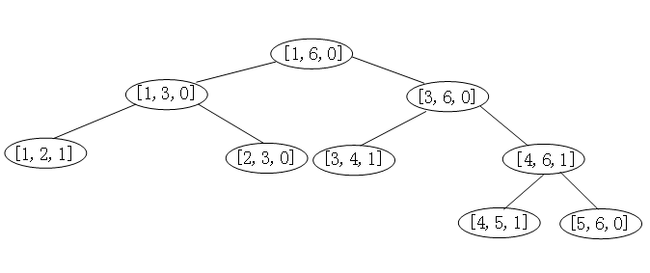
线段树在一些acm题目中经常见到，这种数据结构主要应用在计算几何和地理信息系统中。下图就为一个线段树：

(PS：可能你见过线段树的不同表示方式，但是都大同小异，根据自己的需要来建就行。)

1.线段树基本性质和操作

线段树是一棵二叉树，记为T(a, b)，参数a,b表示区间[a,b]，其中b-a称为区间的长度，记为L。

线段树T(a,b)也可递归定义为：

若L>1 :  [a, (a+b) div 2]为 T的左儿子；

             [(a+b) div 2,b]为T 的右儿子。 

若L=1 : T为叶子节点。

 

线段树中的结点一般采取如下数据结构：

struct Node
{
    int   left,right;  //区间左右值
    Node   *leftchild;
    Node   *rightchild;    
};

线段树的建立：

Node   *build(int   l ,  int r ) //建立二叉树
{
    Node   *root = new Node;
    root->left = l;
    root->right = r;     //设置结点区间
    root->leftchild = NULL;
    root->rightchild = NULL;

    if ( l +1< r )
    {
       int  mid = (r+l) >>1;
       root->leftchild = build ( l , mid ) ;
       root->rightchild = build ( mid  , r) ; 
    } 

    return    root; 
}

线段树中的线段插入和删除：

增加一个cover的域来计算一条线段被覆盖的次数，因此在建立二叉树的时候应顺便把cover置0。

插入一条线段[c,d]：

void  Insert(int  c, int d , Node  *root )
{
       if(c<= root->left&&d>= root->right) 
           root-> cover++;
       else 
       {
           if(c < (root->left+ root->right)/2 ) Insert (c,d, root->leftchild  );
           if(d > (root->left+ root->right)/2 ) Insert (c,d, root->rightchild  );
       }
} 

 

删除一条线段[c,d]:

void  Delete (int c , int  d , Node  *root )
{
       if(c<= root->left&&d>= root->right) 
           root-> cover= root-> cover-1;
       else 
       {
          if(c < (root->left+ root->right)/2 ) Delete ( c,d, root->leftchild  );
          if(d > (root->left+ root->right)/2 ) Delete ( c,d, root->rightchild );
       }
} 

2.线段树的运用

线段树的每个节点上往往都增加了一些其他的域。在这些域中保存了某种动态维护的信息，视不同情况而定。这些域使得线段树具有极大的灵活性，可以适应不同的需求。

例一：

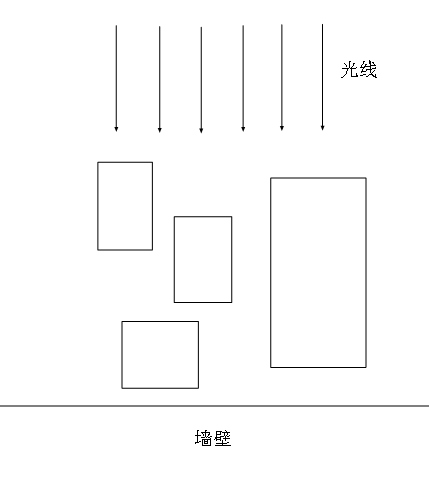
桌子上零散地放着若干个盒子，桌子的后方是一堵墙。如图所示。现在从桌子的前方射来一束平行光， 把盒子的影子投射到了墙上。问影子的总宽度是多少？

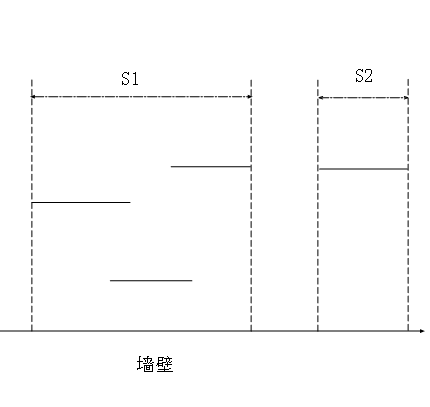
这道题目是一个经典的模型。在这里，我们略去某些处理的步骤，直接分析重点问题，可以把题目抽象地描述如下：x轴上有若干条线段，求线段覆盖的总长度，即S1+S2的长度。

 

2.1最直接的做法：

设线段坐标范围为[min,max]。使用一个下标范围为[min,max-1]的一维数组，其中数组的第i个元素表示[i,i+1]的区间。数组元素初始化全部为0。对于每一条区间为[a,b]的线段，将[a,b]内所有对应的数组元素均设为1。最后统计数组中1的个数即可。

初始     0   0  0  0  0
[1，2]   1   0  0  0  0
[3，5]   1   0  1  1  0
[4，6]   1   0  1  1  1
[5，6]   1   0  1  1  1

其缺点是时间复杂度决定于下标范围的平方，当下标范围很大时（[0,10000]），此方法效率太低。

2.2离散化的做法：

基本思想：先把所有端点坐标从小到大排序，将坐标值与其序号一一对应。这样便可以将原先的坐标值转化为序号后，对其应用前一种算法，再将最后结果转化回来得解。该方法对于线段数相对较少的情况有效。

示例:

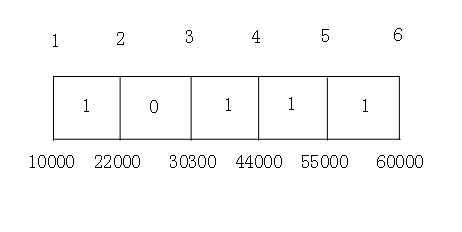
[10000,22000]   [30300,55000]   [44000,60000]   [55000,60000]

排序得10000，22000，30300，44000，55000，60000

对应得1， 2， 3， 4， 5， 6

然后是 [1,2]     [3,5]    [4,6]    [5,6]

初始     0   0  0  0  0
[1，2]   1   0  0  0  0
[3，5]   1   0  1  1  0
[4，6]   1   0  1  1  1
[5，6]   1   0  1  1  1

10000，22000，30300，44000，55000，60000

1，       2，        3，       4，       5，       6

(22000-10000)+(60000-30300)=41700

 

此方法的时间复杂度决定于线段数的平方，对于线段数较多的情况此方法效率太低。

2.3使用线段树的做法：

给线段树每个节点增加一个域cover。cover=1表示该结点所对应的区间被完全覆盖，cover=0表示该结点所对应的区间未被完全覆盖。

如下图的线段树，添加线段[1,2][3,5][4,6]

插入算法：

void   Insert(Node  *root , int  a , int  b)
{
    int m;
    if( root ->cover == 0) 
    { 
        
        m = (root->left+ root->right)/2 ;
        if (a == root->left && b == root->right) 
            root ->cover =1;
        else if (b <= m)  Insert(root->leftchild , a, b);
        else if (a >= m)  Insert(root->rightchild , a, b);
        else 
        {    
                Insert(root->leftchild ,a, m);
                Insert(root->rightchild , m, b);
        }
    }
}

统计算法：

int  Count(Node *root)
{
    int  m,n;
    if (root->cover == 1)
            return   (root-> right - root-> left);
    else if (root-> right - root-> left== 1 )return 0;
    m= Count(root->leftchild);
     n= Count(root->rightchild);
    return m+n;
}

 

 

 

 

---
可以转载, 但必须以超链接形式标明文章原始出处和作者信息及 版权声明

 

原文链接： http://www.cnblogs.com/shuaiwhu/archive/2012/04/22/2464583.html