如何利用BERT做文本摘要

引言

文本摘要是NLP的一个流行的应用，在本文我们会学习如何为一个文本摘要任务微调BERT模型。这种BERT模型一般称为BERTSUM(BERT for summarization)。

有两种不同的文本摘要方法，分别是抽取式(extractive)和生成式(abstractive)。

文本摘要

文本摘要(text summarizatioin)是转换一个长文本到总结(summary)的过程。假设我们有一篇维基百科文章，但是我们不想阅读完整的文章——我们只想该文章的概述。此时，摘要生成可以帮我们得到文本的概述。

文本摘要具有两种方法：

• 抽取式
• 生成式

抽取式

在该方法中，我们从给定的文本中抽取关键句子。举一个例子，考虑下面的维基百科文章：

Machine learning is the study of computer algorithms that improve automatically through experience. It is seen as a subset of artificial intelligence. Machine learning algorithms build a mathematical model based on sample data, known as training data, in order to make predictions or decisions without being explicitly programmed to do so. Machine learning algorithms are used in a wide variety of applications, such as email filtering and computer vision, where it is difficult or infeasible to develop conventional algorithms. 

现在，我们只抽取重要的句子。所以，假设抽取后的结果如下：

Machine learning is the study of computer algorithms that improve automatically through experience. It is seen as a subset of artificial intelligence. Machine learning algorithms are used in a wide variety of applications, such as email filtering and computer vision, where it is difficult or infeasible to develop conventional algorithms. 

即我们可以得到保持给定文本大体意思的句子。

生成式

在生成式方法中，我们不是从原文中抽取句子。而是，通过对原文进行释义(paraphrasing)生成一个总结。释义的意思是我们通过另一种更清晰的方式使用不同的单词来重新表达给定的文本。同时生成的句子也是只包含原文的重要信息。

也看一个例子，假设使用上面小节同样的文章：

Machine learning is the study of computer algorithms that improve automatically through experience. It is seen as a subset of artificial intelligence. Machine learning algorithms build a mathematical model based on sample data, known as training data, in order to make predictions or decisions without being explicitly programmed to do so. Machine learning algorithms are used in a wide variety of applications, such as email filtering and computer vision, where it is difficult or infeasible to develop conventional algorithms. 

现在，通过生成式方法，我们通过释义生成总结如下：

Machine learning is a subset of artificial intelligence and it is widely used for creating a variety of applications such as email filtering and computer vision. 

从结果可以看到，基本上保留了文本的关键信息。

为文本摘要微调BERT

首先来看如何做抽取式摘要。

使用BERT做抽取式摘要

为了做抽取式摘要，我们需要微调下BERT模型输入数据格式。在此之前，我们先回顾下如何将输入数据喂给BERT模型。

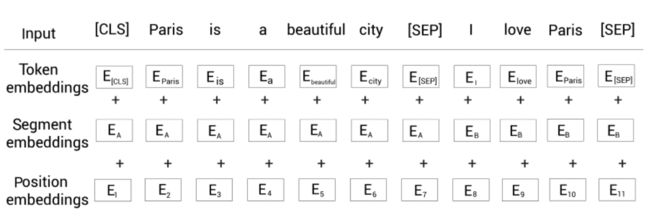
假设我们有两个句子：Paris is a beautiful city. I love Paris. 。

首先我们对句子进行分词，然后为句子开头增加[CLS]标记，为句子结尾增加[SEP]标记。然后将这些单词输入到三个嵌入层：标记嵌入、片段嵌入和位置嵌入。

BERT模型接收这些输入，然后输出每个标记的表示：

那么我们如何将BERT应用到文本摘要任务？

我们知道BERT可以得到每个标记的表示，但在这里我们不需要每个标记的表示，而是每个句子的表示。

因为抽取式摘要只是选择重要的句子。如果我们能得到每个句子的表示，我们就能把句子的表示输入到一个分类器中，让分类器告诉我们该句子是否重要。

那么，问题是我们如何得到句子的表示？我们能否使用[CLS]标记对应的表示作为句子的表示？是的！但这里有一个小问题。我们只在第一个句子的开头添加[ CLS ]标记，但是在文本摘要任务中，我们给 BERT 模型输入多个句子，我们需要所有句子的表示。

因此，我们修改输入数据格式。为每个句子的开头都增加[CLS]标记，这样我们就能通过此标记得到每个句子的表示。

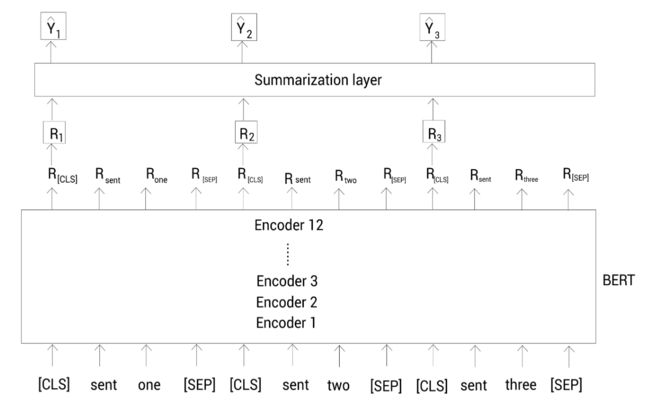
假设我们有三个句子：sent one, sent two和sent three。首先当然是进行分词，然后为每个句子开头增加[CLS]标记。同时我们也通过[SEP]来分开每个句子：

Input tokens = [ [CLS], sent, one, [SEP], [CLS], sent, two, [SEP], [CLS], sent, three, [SEP] ]

然后，我们将这些单词输入到标记、片段和位置嵌入层。标记嵌入层如下所示：

下一层是片段嵌入层。我们知道片段嵌入层用于区分两个给定的句子，返回两个句子的嵌入$E_A$或$E_B$。但是在文本摘要设定中，我们会输入不只两个句子。那我们如何进行映射呢？

此时，我们使用一个间隔(interval)片段嵌入。间隔片段嵌入用于区分给定的多个句子，我们映射出现在奇数索引句子中的单词到$E_A$，映射偶数索引到$E_B$。假设我们有四个句子：

• 句子1中的所有单词被映射到$E_A$
• 句子2中的所有单词被映射到$E_B$
• 句子3中的所有单词被映射到$E_A$
• 句子4中的所有单词被映射到$E_B$

间隔片段嵌入层如下图所示：

下一层就是位置编码嵌入层，它编码了输入中单词的位置信息：

对上面的步骤进行一个总结：

然后我们将修改格式后的输入喂给BERT模型。如下图所示，BERT模型接收该输入，并输出每个标记的表示。因为我们为每个句子增加了[CLS]标记，我们可以使用该标记作为句子的表示。比如下图中的$R_1$代表了sent one；$R_2$代表了sent two。我们称这种BERT模型为BERTSUM。

注意，为了得到句子表示，我们不必从头训练BERT。我们可以使用任一预训练的BERT模型，只要按照上面的做法修改输入格式。然后就可以用每个句子开头的[CLS]标记代表整个句子表示。

带分类器的BERTSUM

我们知道在抽取式摘要中，我们只要选择重要的句子。我们从上文已经知道如何获得句子的表示。现在，我们将这些表示输入一个简单的二分类器，来判断输入的句子是否能被加入到摘要中。该分类器层通常被称为摘要层：

该分类器返回每个句子能加到摘要中的概率。

对于文档中的每个句子$i$，我们会得到句子表示$R_i$，然后输入到摘要层，得到能加到摘要中的概率${\hat{Y}}_i$：
$${\hat{Y}}_i=\sigma (W_o{R}_i+b_o)$$
显然，只需要一个Sigmoid分类器就能计算这个概率。通过最小化真实概率$Y_i$和预测概率${\hat{Y}}_i$之间的二分类损失，我们可以同时微调预训练的BERT模型和摘要层。

但除了简单的Sigmoid分类器，我们还可以尝试其他的分类器。

BERTSUM和一个Transfomer及LSTM

学者们提出了另外两种不同的方法：

• 一个句间(inter-sentence)Transformer
• LSTM

即，不是将句子表示$R$直接输入到一个sigmoid分类器，而是输入到一个Transformer和LSTM来得到更好的表示。

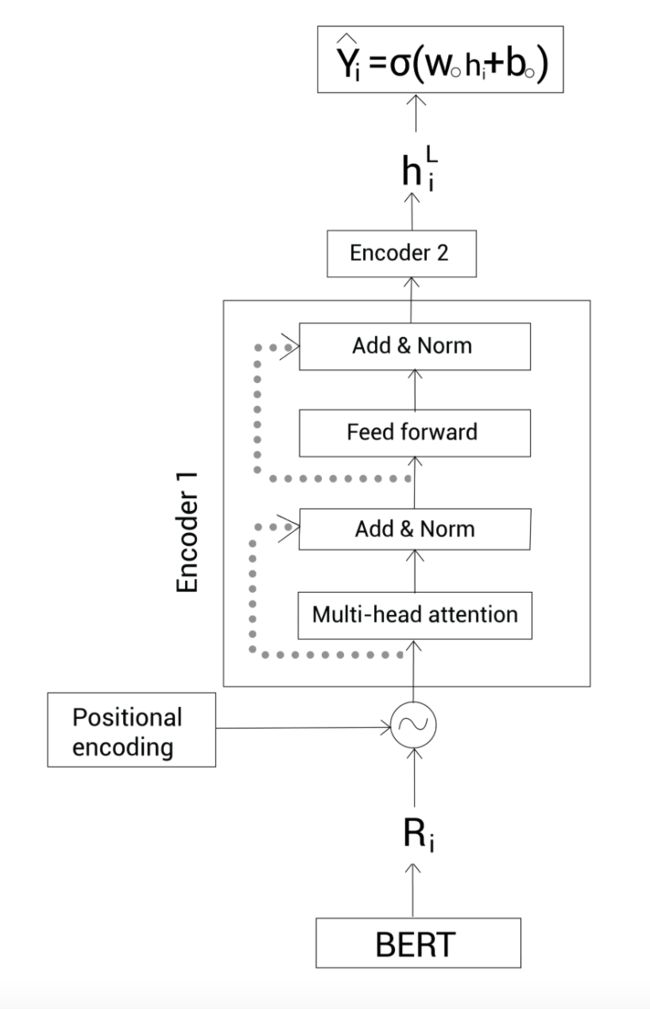
带有句间Transformer的BERTSUM

有了句间Transformer，我们可以将之前BERT的结果输入给Transformer编码器层。但是为啥要这么做么？Transformer的编码器接收表示$R$，然后返回它的隐藏状态表示。该隐藏状态表示有助于学习注重于摘要任务的文档级特征。

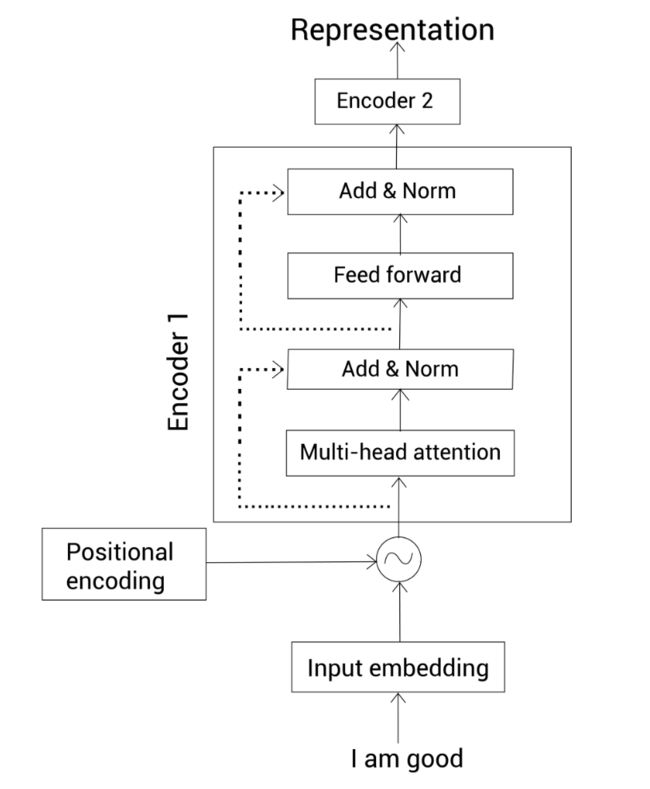
我们先回顾下transformer的编码器。我们知道transformer包含$L$个编码器。每个编码器由两个子层组成——多头注意力和带层归一化的前馈网络。下图显示了两个编码器(只有第一个是展开了的)。最顶层的编码器输出隐藏状态表示：

我们来理解transformer编码器在这里起的作用。我们知道transformer包含$L$个编码器。

用$h$表示由transformer编码器得到的隐藏状态表示，那么$h^l$表示由编码器$l$得到的。

我们输入从BERT得到的表示$R$​到transformer编码器中，但在输入到编码器之前，我们增加位置嵌入。

输入表示$R$经过位置嵌入得到的嵌入表示记为$h^0$：
$$h^0=\text{PosEmb}(R)$$
$\text{PosEmb}$表示位置嵌入层。现在，我们将$h^0$喂给编码器。每个编码器包含两个子层——多头注意力层和前馈网络层。对于编码器$l$​，两个子层的公式为：
$$\begin{gathered} {\tilde{h}}^l=\text{LN}(h^{l-1}+\text{MHAtt}(h^{l-1})) \\ {h}^l=\text{LN}({\tilde{h}}^l+\text{FNN}({\tilde{h}}^l)) \end{gathered}$$
这里$\text{LN}$代表层归一化；$\text{MHAtt}$代表多头注意力；$\text{FNN}$代表前馈网络。

最顶层由$L$表示，那么由最顶层编码器得到的隐藏状态表示记为$h^L$。我们拿到这个隐藏状态表示$h^L$​再喂给sigmoid分类器，得到了句子属于摘要的概率：
$${\hat{Y}}_i=\sigma (W_o{h}_i^L+b_o)$$
整个架构如下：

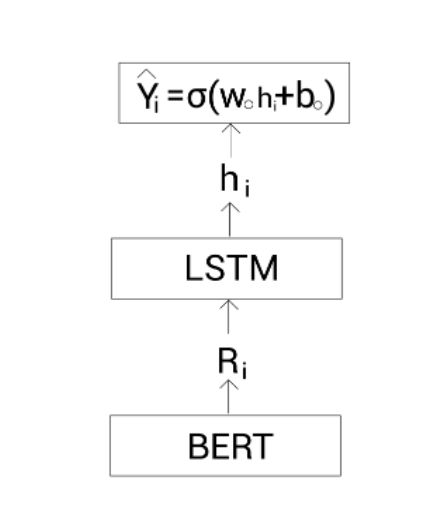
带LSTM的BERTSUM

我们拿从BERT模型得到的句子$i$表示$R_i$喂给LSTM单元。LSTM单元输出隐藏状态$h_i$。然后还是将该隐藏状态输入到一个sigmoid分类器中：
$${\hat{Y}}_i=\sigma (W_o{h}_i+b_o)$$
这种方法就简单多了，其架构为：

利用BERT做生成式摘要

在生成式摘要中，我们的目标是通过释义创建一个摘要。那我们要如何利用BERT来做这件事呢？由于BERT仅返回每个标记的表示。如何利用BERT来生成新文本呢？

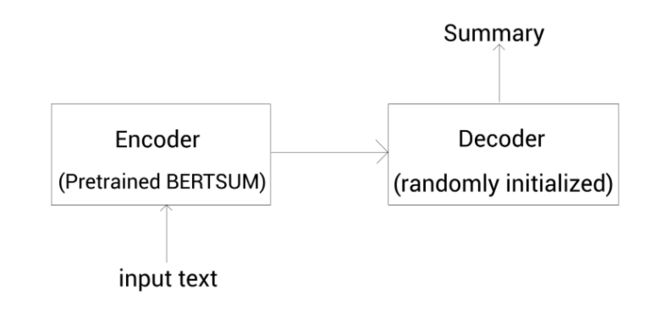
为了做生成式摘要，我们使用带编码器-解码器的transformer模型。我们输入文本到编码器，输出给定文本的表示。然后将该表示输入到解码器，解码器基于该表示来生成摘要。

在这里，我们可以使用预训练的BERTSUM作为编码器。但有一个小问题：在transformer模型中，编码器是一个预训练的BERTSUM模型，但解码器是随机初始化的。这会在训练过程产生差异。因为编码器已经是预训练的，它可能会过拟合；而解码器不是预训练的，它可能会欠拟合。

所以，我们解决这个问题。我们需要使用两个Adam优化器，分别用于编码器和解码器。并且使用不同的学习率。因为编码器已经预训练了，我们可以设置一个小一点的学习率和平滑一点的decay。编码器的学习率给定为：
$$l{r}_e=\widetilde{l{r}_e}.\min ({\text{step}}^{-0.5},\text{step}.{\text{warmup}}_e^{-15})$$
其中$\widetilde{l{r}_e}=2e^{-3}$；${\text{warmup}}_e=20000$。

而解码器的学习率给定如下：
$$l{r}_d=\widetilde{l{r}_d}.\min ({\text{step}}^{-0.5},\text{step}.{\text{warmup}}_d^{-15})$$
其中$\widetilde{l{r}_d}=0.1$；${\text{warmup}}_d=10000$。

生成式摘要的过程如下图所示：

我们称该模型为BERTSUMABS(BERT for abstractive summarization)。

我们下面来看下如何评估BERTSUM模型的表现。

理解ROUGE评估指标

ROUGE是Recall-Oriented Understudy for Gisting Evaluation的简称，主要基于召回率的。有五种不同的ROUGE指标：

• ROUGE-N
• ROUGE-L
• ROUGE-W
• ROUGE-S
• ROUGE-SU

我们只关注ROUGE-N和ROUGE-L。

理解ROUGE-N指标

ROUGE-N统计在候选摘要(预测的)和引用摘要(实际的)之间的召回率。

召回率定义为在候选摘要和引用摘要之间重叠的n-gram总数除以引用摘要的n-gram总数。

ROUGE-1

那么ROUGE-1就是候选摘要和引用摘要之间的unigram召回率。考虑下面的例子：

• 候选摘要： Machine learning is seen as a subset of artificial intelligence.
• 引用摘要：Machine Learning is a subset of artificial intelligence.

那么我们可以计算ROUGE-1为：
$$\text{Recall}=\frac{\text{重叠的unigram总数}}{\text{引用中的unigram总数}}$$
候选和引用摘要中的unigram项如下：

• 候选：Machine, learning, is, seen, as, a, subset, of, artificial, intelligence
• 引用：Machine, Learning, is, a, subset, of, artificial, intelligence.

可以看到重叠的unigram总数为$8$；而引用中的unigram总数也为$8$。所以，召回率为：
$$\text{Recall}=8/8=1$$
下面我们看下如何计算ROUGE-2。

ROUGE-2

ROUGE-2那么就是候选和引用摘要之间的bigram召回率。我们看上面同样的例子：

• 候选摘要： Machine learning is seen as a subset of artificial intelligence
• 引用摘要：Machine Learning is a subset of artificial intelligence

那么ROUGE-2计算如下：
$$\text{Recall}=\frac{\text{重叠的bigram总数}}{\text{引用中的bigram总数}}$$
候选和引用摘要中的bigram总数为：

• 候选：(machine learning), (learning is), (is seen), (seen as), (as a), (a subset), (subset of), (of artificial) (artificial intelligence)
• 引用：(machine learning), (learning is), (is a), (a subset), (subset of), (of artificial) (artificial intelligence)

可以看到重叠的bigram总数为$6$；而引用摘要中的总bigram数量为$7$。我们可以得到：
$$\text{Recall}=6/7=0.85$$
这样我们就得到了ROUGE-2分数为0.85，以此类推，我们可以计算ROUGE-N。

理解ROUGE-L指标

ROUGE-L基于最长公共子序列(LCS, longest common subsequence)。两个序列间的LCS是长度最大的相同子序列。所以，如何候选和引用摘要之间有一个LCS，那么我们可以说候选摘要匹配了引用摘要。

ROUGE-L指标考虑了召回率和准确率(Recision)。

召回率$R_{lcs}$计算为候选摘要和引用摘要的LCS除以引用摘要中的单词总数：
$$R_{lcs}=\frac{\text{LCS(候选摘要，引用摘要)}}{\text{引用摘要单词总数}}$$
准确率$P_{lcs}$计算为候选摘要和引用摘要的LCS除以候选摘要中的单词总数：
$$P_{lcs}=\frac{\text{LCS(候选摘要，引用摘要)}}{\text{候选摘要单词总数}}$$
那么最终代表ROUGE-L指标的$F_{lcs}$计算如下：
$$F_{lcs}=\frac{(1+b{)}^2{R}_{lcs}{P}_{lcs}}{R_{lcs}+b^2{P}_{lcs}}$$
$b$用于均衡准确率和召回率之间的重要性。

BERTSUM模型的表现

BERTSUM的研究者们使用CNN/DailyMain新闻数据集，我们将该数据集分为训练和测试。然后基于训练数据集训练模型，并在测试集上评估。

下表显示了我们介绍的三种不同抽取式摘要的BERTSUM模型表现：

Model	ROUGE-1	ROUGE-2	ROUGE-L
BERT+classifier	42.23	20.22	39.60
BERT+transformer	43.25	20.24	39.63
BERT+LSTM	43.22	20.17	39.59

可以看到BERT+transformer的结果要略好一点。

下面看下生成式摘要BERTSUMABS的表现：

Model	ROUGE-1	ROUGE-2	ROUGE-L
BERTSUMABS	41.72	19.39	38.76

References

1. Getting Started with Google BERT