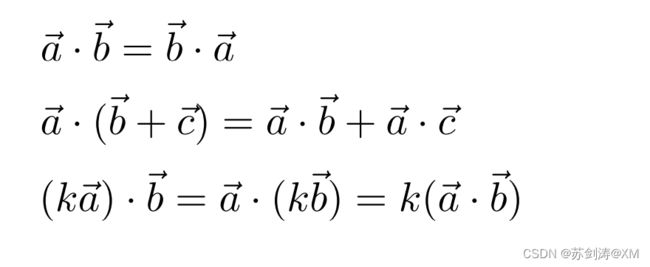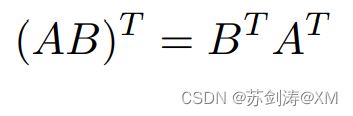计算机图形学入门-线性代数复习

本专栏内容整理了GAMES101的计算机图形学课程的主要内容，作为我学习计算机图形学的一份复习备份或叫做笔记。内容中如有错误，或有其他建议，欢迎大家指出。

附上GAMES101计算机图形学课程：GAMES101: 现代计算机图形学入门https://sites.cs.ucsb.edu/~lingqi/teaching/games101.html

GAMES101-现代计算机图形学入门-闫令琪_哔哩哔哩_bilibiliGAMES101-现代计算机图形学入门-闫令琪共计23条视频，包括：Lecture 01 Overview of Computer Graphics、Lecture 02 Review of Linear Algebra、Lecture 03 Transformation等，UP主更多精彩视频，请关注UP账号。https://www.bilibili.com/video/BV1X7411F744

计算机图形学中更依赖线性代数，主要使用到：向量的点乘，叉乘，向量 x 矩阵描述变换：如向量的平移和旋转操作可以用向量乘矩阵来表示；

向量（Vectors）

有方向有大小的量
方向：A->B :   = B - A；
长度：|| ||
向量平移后表示的是同一个向量

单位向量（长度为1的向量）： =  / ||a||,图形学里表示方向时都用单位向量表示，不用关心它的长度

向量加法：三角形法则  + =  , 平移后面的向量使其开始跟前面的向量的结束重合，再由前面的向量的开始指向后一个向量的结束；

图形学中笛卡尔坐标系中向量的表示：，（0,0）固定是所有向量的起点（x,y）是终点

向量的点乘：

   

几何意义：是一条边向另一条边的投影乘以另一条边的长度。

 向量点乘满足交换律，结合律，和分配律

 

 向量点乘的计算描述：对应的项相乘然后加起来

 向量点乘在图形学中的作用：
        求两个向量的夹角；
        求一个向量在另一个向量上的投影；
        做向量的垂直 分解；
        判断方向性：方向基本一致：点积>0;   方向基本相反：点积<0;   向量相互垂直：点积=0；（锐角、钝角、直角）

向量叉乘

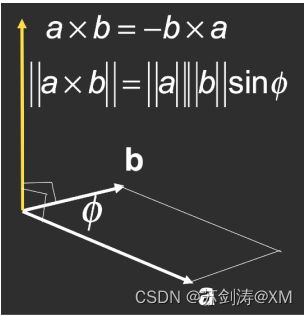
叉乘结果：两个参与叉乘的向量（a , b）得到一个新的向量 ( c )，且该向量( c )垂直于参与叉乘的两个向量(a , b)；结果向量（c）的方向由右手定则可以判断；
右手定则：右手掌心由 a 旋转到 b ，得到大拇指所指方向即是叉积向量的方向；

||  || = |||| |||| sin

                                       

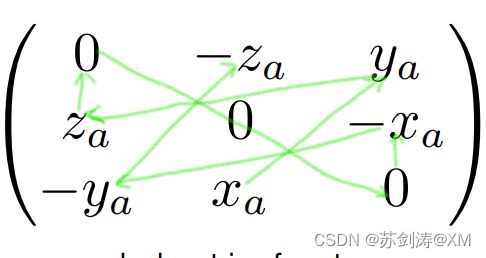
怎么算：

 用手机的连线解锁 由 Xa -> Ya -> Za -> 0 ,0 ,0 -> -Xa -> -Ya -> -Za方便记住

向量叉乘的作用：
用于构建坐标系；
当a是单位向量时，计算b终点到a所在直线的距离；
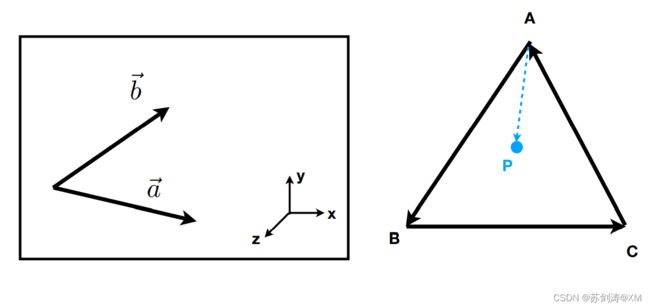
在二维空间中，aXb等于由向量a和向量b构成的平行四边形的面积。
判断两向量的左右关系：即判断叉积的正负，a x b = +c ==> b在a的左侧；a在b的右侧
判断一个点是否在某个多边形内部:判断点是否都在每条边的左边，或者是否都在右边，是则表示点在多边形内部,图形学中光栅化时需要判断

 

AB x AP = +  ==>P在AB的左侧；
BC x BP = +  ==>P在BC的左侧；
CA x CP = +  ==>P在CA的左侧；所以P在三角形ABC内；

矩阵（Matrices）

矩阵就是一堆数，把这堆数安排在一个平面内，再按照m行n列来排列构成m  n 的矩阵；矩阵在图形学中最大的应用就是描述变换；

矩阵的乘积

A，B 两个矩阵要相乘 ,必须满足 A的行数量 == B的列数量，结果矩阵是一个有A的行数和B的列数的矩阵；结果矩阵中的元素(i, j)为A的第i行和B的第j列的点积;

如：下图结果矩阵中第2行第3列的值是 A的第二行第一个数：5 乘以 B的第三列第一个数：9 加上A的第二行第二个数：2 乘以 B的第三列第二个数：8 
即：5 x 9 + 2 x 8 = 61;
(M x N) (N x P) = (M x P)

 ​​​​​​

 图中空缺处：1 x 6 + 3 x 7 = 27;   0 x 4 + 4 x 3 = 12

 矩阵乘积的性质：
   没有任何交换律: AB !== BA; （先旋转再平移和先平移再旋转的结果是不一样的； 矩阵描述的旋转都是围绕原点旋转）
   有结合律和分配律：(AB)C=A(BC) ； A(B+C) = AB + AC； （A+B)C = AC + BC；

矩阵的转置：
m行n列的矩阵变为n行m列的矩阵；

性质：对乘积的转置，需要分别对两个矩阵转置再乘积；

 单位矩阵： 矩阵右上到左下那条都是1，其他的元素都是0。任何矩阵与单位矩阵相乘都等于本身

 逆矩阵：两个矩阵的乘积是单位矩阵。则称这两个矩阵互逆；

正交矩阵：矩阵的逆矩阵正好是它的转置,则矩阵A称为正交矩阵;
                  A = 
 

矩阵向量乘法

始终将向量视为列矩阵(m×1)，m是向量的维数。矩阵始终要在向量的左侧，列向量始终在最右侧。列向量的变换中。按顺序变换的各个矩阵都在列向量左侧，从右到左按变换的先后的顺序排列排列，也就是说越靠近列向量的矩阵越先发生变换；

下面的运算描述向量（x,y）按y轴进行对称映射

 向量点乘的矩阵表示：

下一篇：变形！！额，是变换！计算机图形学入门-变换_苏剑涛@XM的博客-CSDN博客