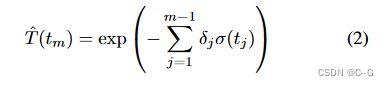74、Beyond RGB: Scene-Property Synthesis with Neural Radiance Fields
简介
- List item
论文地址:http://arxiv-export3.library.cornell.edu/abs/2206.04669v1
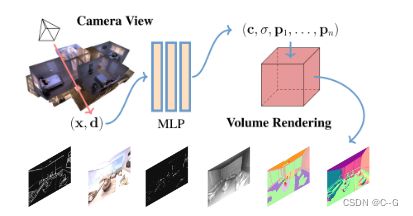
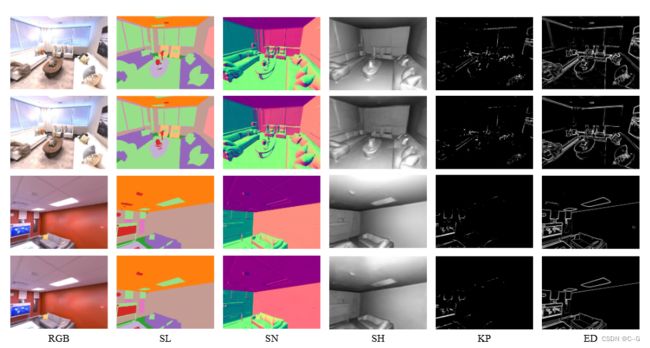
利用隐式三维表示和神经渲染的最新进展,从综合模型的角度提供了一种新的场景理解方法,能够从新颖的视点渲染照片逼真的RGB图像,而且还能够渲染各种精确的场景属性(例如,外观、几何和语义)。便于在统一的框架下解决各种场景理解任务,包括语义分割、表面法向估计、重塑、关键点检测和边缘检测。可以成为生成式学习和判别学习的强大工具,因此有利于研究广泛的有趣问题,例如研究综合范式中的任务关系,将知识转移到新任务中,促进下游判别任务作为数据增强的方式,以及作为数据创建的自动标签器
贡献点:
- 从学习合成模型的角度提出了一种新的解决方案SS-NeRF来进行场景理解。SS-NeRF是第一个将NeRF扩展到同时渲染照片逼真的新视图图像和各种相应的场景属性的工作
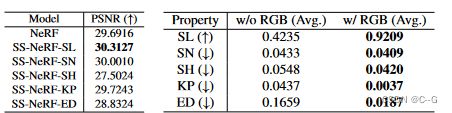
- 实例化SS-NeRF与五个流行的场景属性,包括语义标签,表面法线,阴影,关键点,和边缘。作为一种通用的神经场景表示,SSNeRF被证明优于一种混合策略,该策略分别训练NeRF(用于渲染图像)和特定于任务的判别模型(用于预测场景属性)
- SS-NeRF框架是连接生成式学习和判别式学习的强大工具,为通过综合范式中的多任务学习或知识迁移来研究不同属性和任务之间的关系带来了新的见解
- SS-NeRF可以有利于各种问题,例如促进下游任务作为数据增强的方式,并作为数据创建的自动标签器
实现流程
Innovation and Problem Setting
NeRF使用感知器网络学习隐式3D几何和场景表示,这种几何感知的表示不仅适用于RGB颜色,而且还适用于其他场景属性,因为它是内部共享的。这种表示方法同时解决了判别模型(泛化到新视图)和基于gan的生成模型(泛化从图像合成到其他任务)的局限性。它为场景理解提供了一个新的合成视角,并为广泛的应用带来了新的潜力
对于某个场景属性 P i P_i Pi,目标是学习一个函数 f i f_i fi 来估计它在每个3D位置和视图方向上的值 p i p_i pi : f i ( x , d ) → p i f_i(x, d) → p_i fi(x,d)→pi
隐式函数编码了场景的几何、形状和纹理信息,这些信息在不同的属性预测任务中是可共享的,不同的属性可以通过共享知识一起学习
那么可以扩展为给定 K 个场景属性的集合 P = P k K = 1 K P = {P_k}^K_{K =1} P=PkK=1K,目标是构建一个表示函数 f,它可以将三维坐标和视图方向映射到相应的属性值 f ( x , d ) → { P k } K = 1 K f (x, d) →\{P_k\}^K_{K =1} f(x,d)→{Pk}K=1K

采用共享位置编码器 F e n c F_{enc} Fenc 为3D坐标(x, y, z)构建特征嵌入 e x e_x ex
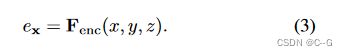
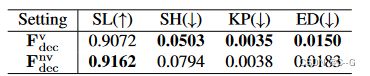
采用了 F d e c v F^v_{dec} Fdecv 和 F d e c n v F^{nv}_{dec} Fdecnv 两种解码网络
F d e c v F^v_{dec} Fdecv 将附加视图输入 d = (θ, φ) 与编码后的坐标一起进行属性 P i v P^v_i Piv 的预测,
F d e c n v F^{nv}_{dec} Fdecnv 则直接用编码后的坐标预测场景属性 P j n v P^{nv}_j Pjnv
![]()
密度 σ 总是需要为单个属性或多个属性进行体渲染,颜色是信息量最大的场景属性,将它们作为SS-NeRF模型的固定输出,并在这个基本模型上添加其他属性
Instantiation and Optimization of SS-NeRF
F d e c v F^v_{dec} Fdecv 预测 底纹(SH), 关键点(KP), 和 边缘(ED), F d e c n v F^{nv}_{dec} Fdecnv 语义标签(SL) 和 表面法线(SN)
SS-NeRF优化过程中,采用分层体积采样策略,随机选择一些“粗”样本点,然后对偏向于体积相关部分的“细”点进行更明智的抽样,彩色图像合成,采用均方误差(MSE)

p ( r ) 、 p ^ c ( r ) 、 p ^ f ( r ) p(r)、\hat{p}_c(r)、\hat{p}_f (r) p(r)、p^c(r)、p^f(r) 分别为属性 p 的真相、粗体积预测和精细体积预测,R是每一批射线 r 的集合,MSE损失也用于表面法向预测,对于语义标签预测,使用交叉熵损失函数
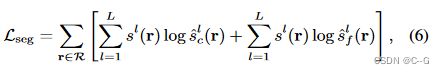
s l 、 s ^ c l 、 s ^ f l s^l、\hat{s}^l_c 、\hat{s}^l_f sl、s^cl、s^fl 分别为 l 类多类语义概率的真值、粗体积预测和细体积预测
对 粗、细预测 s ^ c l 、 s ^ f l \hat{s}^l_c、\hat{s}^l_f s^cl、s^fl 进行体绘制后使用softmax处理。
对于阴影、关键点和边缘,采用 L 1 L_1 L1 损失
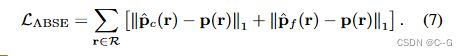
最终损耗为特定任务的光测损耗与标准损耗的加权和,为:.
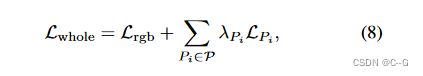
其中 P = { P S L , P S N , P S H , P K P , P E D } P = \{P_{SL}, P_{SN}, P_{SH}, P_{KP}, P_{ED}\} P={PSL,PSN,PSH,PKP,PED} 为性质集, λ P i λ_{P_i} λPi 为相应的权值
在所有的五个场景属性中,表面法线是一个特殊的矢量形式,它在图像中的投影取决于相机的姿势。为了更好地模拟这一特性,使用 F d e c n v F^{nv}_{dec} Fdecnv 作为解码网络,并引入编码后的相机姿态的额外输入,用体绘制技术直接合成编码后的法线
表面法线由深度 S N ( x , y , z ) = ( − d x d z , − d y d z , 1 ) SN (x, y, z) =(− \frac{dx}{dz},−\frac{dy}{dz}, 1) SN(x,y,z)=(−dzdx,−dzdy,1) 得到,其中(x, y, z)是三维坐标, d x d z , d y d z \frac{dx}{dz},\frac{dy}{dz} dzdx,dzdy分别是z相对于 x 和 y 的梯度。
边缘由Canny检测器渲染,关键点来源于SURF,阴影由预先训练的模型XTConsistency渲染
实验
λ S N = 1 , λ S L = 0.04 , λ S H = 0.1 , λ K P = 2 , λ E D = 0.4 λ_{SN} = 1, λ_{SL} = 0.04, λ_{SH} = 0.1, λ_{KP} = 2, λ_{ED} = 0.4 λSN=1,λSL=0.04,λSH=0.1,λKP=2,λED=0.4
使用Adam优化器,学习率为 5 × 1 0 − 4 5 \times 10^{-4} 5×10−4, β 1 = 0.9 , β 2 = 0.999 \beta_1 = 0.9,\beta_2 = 0.999 β1=0.9,β2=0.999,每个场景使用 200k 迭代,在单个NVIDIA RTX 2080 Ti GPU上花费9小时训练