Pytorch中常用的四种优化器SGD、Momentum、RMSProp、Adam
来源：AINLPer微信公众号 （点击了解一下吧）
编辑: ShuYini
校稿: ShuYini
时间: 2019-8-16
引言
很多人在使用pytorch的时候都会遇到优化器选择的问题，今天就给大家介绍对比一下pytorch中常用的四种优化器。SGD、Momentum、RMSProp、Adam。
随机梯度下降法（SGD）
算法介绍
对比批量梯度下降法，假设从一批训练样本 n n n中随机选取一个样本 i s i_s is。模型参数为 W W W，代价函数为 J ( W ) J(W) J(W)，梯度为 Δ J ( W ) ΔJ(W) ΔJ(W)，学习率为 η t η_t ηt，则使用随机梯度下降法更新参数表达式为：
W t + 1 = W t − η t g t W_{t+1}=W_t−η_tg_t Wt+1=Wt−ηtgt 其中， g t = Δ J i s ( W t ; X ( i s ) ; X ( i s ) ) g_t=ΔJ_{i_s}(W_t;X^{(i_s)};X^{(i_s)}) gt=ΔJis(Wt;X(is);X(is)), i s ∈ 1 , 2 , . . . , n i_s∈{1,2,...,n} is∈1,2,...,n表示随机选择的一个梯度方向， W t W_t Wt表示t时刻的模型参数。 E ( g t ) = Δ J ( W t ) E(g_t)=ΔJ(W_t) E(gt)=ΔJ(Wt)，这里虽然引入了随机性和噪声，但期望仍然等于正确的梯度下降。
基本策略可以理解为随机梯度下降像是一个盲人下山，不用每走一步计算一次梯度，但是他总能下到山底，只不过过程会显得扭扭曲曲。
算法评价
优点:
虽然SGD需要走很多步的样子，但是对梯度的要求很低（计算梯度快）。而对于引入噪声，大量的理论和实践工作证明，只要噪声不是特别大，SGD都能很好地收敛。应用大型数据集时，训练速度很快。比如每次从百万数据样本中，取几百个数据点，算一个SGD梯度，更新一下模型参数。相比于标准梯度下降法的遍历全部样本，每输入一个样本更新一次参数，要快得多。
缺点:
SGD在随机选择梯度的同时会引入噪声，使得权值更新的方向不一定正确。此外，SGD也没能单独克服局部最优解的问题。
标准动量优化算法（Momentum）
算法介绍
使用动量(Momentum)的随机梯度下降法(SGD)，主要思想是引入一个积攒历史梯度信息动量来加速SGD。从训练集中取一个大小为n的小批量 X ( 1 ) , X ( 2 ) , . . . , X ( n ) {X^{(1)},X^{(2)},...,X^{(n)}} X(1),X(2),...,X(n)样本，对应的真实值分别为 Y ( i ) Y(i) Y(i)，则Momentum优化表达式为：
L ( Y , f ( X ) ) = { v t = α v t − 1 + η t Δ J ( W t , X ( i s ) , Y ( i s ) ) W t + 1 = W t − v t L(Y,f(X)) = \begin{cases} v_t=αv_t−1+η_tΔJ(W_t,X^{(i_s)},Y^{(i_s)}) \\ W_{t+1}=W_t−v_t \end{cases} L(Y,f(X))={vt=αvt−1+ηtΔJ(Wt,X(is),Y(is))Wt+1=Wt−vt 其中， v t v_t vt表示t时刻积攒的加速度。α表示动力的大小，一般取值为0.9（表示最大速度10倍于SGD）。 Δ J ( W t , X ( i s ) , Y ( i s ) ) ΔJ(W_t,X^{(i_s)},Y^{(i_s)}) ΔJ(Wt,X(is),Y(is))含义见SGD算法。 W t W_t Wt表示t时刻模型参数。
算法的理解
动量主要解决SGD的两个问题：一是随机梯度的方法（引入的噪声）；二是Hessian矩阵病态问题（可以理解为SGD在收敛过程中和正确梯度相比来回摆动比较大的问题）。
简单理解：由于当前权值的改变会受到上一次权值改变的影响，类似于小球向下滚动的时候带上了惯性。这样可以加快小球向下滚动的速度。
RMSProp算法
算法介绍
与动量梯度下降一样，都是消除梯度下降过程中的摆动来加速梯度下降的方法。 梯度更新公式：
更新权重的时候，使用除根号的方法，可以使较大的梯度大幅度变小，而较小的梯度小幅度变小，这样就可以使较大梯度方向上的波动小下来，那么整个梯度下降的过程中摆动就会比较小，就能设置较大的learning-rate，使得学习步子变大，达到加快学习的目的。
在实际的应用中，权重W或者b往往是很多维度权重集合，就是多维的，在进行除根号操作中，会将其中大的维度的梯度大幅降低，不是说权重W变化趋势一样。
RMSProp算法在经验上已经被证明是一种有效且实用的深度神经网络优化算法。目前它是深度学习从业者经常采用的优化方法之一。
Adam算法
算法介绍
Adam中动量直接并入了梯度一阶矩（指数加权）的估计。其次，相比于缺少修正因子导致二阶矩估计可能在训练初期具有很高偏置的RMSProp，Adam包括偏置修正，修正从原点初始化的一阶矩（动量项）和（非中心的）二阶矩估计。Adam算法策略可以表示为：
其中， m t m_t mt和 v t v_t vt分别为一阶动量项和二阶动量项。 β 1 , β 2 β_1,β_2 β1,β2为动力值大小通常分别取0.9和0.999； m t ^ \hat{m_t} mt^, v t ^ \hat{v_t} vt^分别为各自的修正值。 W t W_t Wt表示t时刻即第t迭代模型的参数， g t = Δ J ( W t ) g_t=ΔJ(W_t) gt=ΔJ(Wt)表示t次迭代代价函数关于W的梯度大小；ϵ是一个取值很小的数（一般为1e-8）为了避免分母为0。
算法分析
该方法和RMSProp很像，除了使用的是平滑版的梯度m，而不是原始梯度dx。推荐参数值eps=1e-8, beta1=0.9, beta2=0.999。在实际操作中，推荐Adam作为默认算法，一般比RMSProp要好一点。
算法比较
为了验证四种算法的性能，在pytorch中的对同一个网络进行优化，比较四种算法损失函数随着时间的变化情况。代码如下：
opt_SGD=torch.optim.SGD(net_SGD.parameters(),lr=LR)
opt_Momentum=torch.optim.SGD(net_Momentum.parameters(),lr=LR,momentum=0.8)
opt_RMSprop=torch.optim.RMSprop(net_RMSprop.parameters(),lr=LR,alpha=0.9)
opt_Adam=torch.optim.Adam(net_Adam.parameters(),lr=LR,betas=(0.9,0.99))
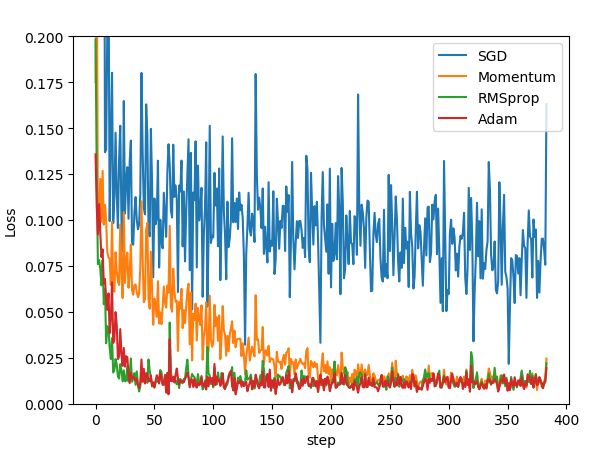SGD 是最普通的优化器, 也可以说没有加速效果, 而 Momentum 是 SGD 的改良版, 它加入了动量原则. 后面的 RMSprop 又是 Momentum 的升级版. 而 Adam 又是 RMSprop 的升级版. 不过从这个结果中我们看到, Adam 的效果似乎比 RMSprop 要差一点. 所以说并不是越先进的优化器, 结果越佳。
参考：
https://blog.csdn.net/weixin_40170902/article/details/80092628
更多自然语言处理、pytorch相关知识，还请关注 AINLPer 公众号，极品干货即刻送达。