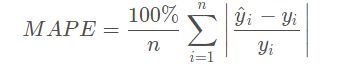【数据分析】如何量化时间序列之间的相似性？

如何量化时间序列之间的相似性

逝者如斯夫，不舍昼夜。时间不会停止，世界上的一切都在不断运动。抛开物理学或哲学的概念不提，几乎所有东西都可以被描述为一系列的事件。对数据更感兴趣的人来说，它们又可以被看做是一系列的测量，这就是我们所说的时间序列。一个时间序列可以包含关于生活中许多不同方面的各种信息，如每天的温度曲线、货币汇率和股票评级、飞机的速度和位置、海洋潮汐水平高度······

本篇博文中，我们将看看我们是如何决定哪些时间序列是相似的，哪些是不相似的——这是一个在开始解决总体问题之前，需要考虑的重要问题。在下图中，可以看到一组不同的时间序列，我们将使用不同的（不）相似度量来相互比较。这些序列都是对同一消费曲线（一个电表冬季一周的平均消费）的描述。然而，下面介绍的方法具有高度概括性，适用于多个行业的不同问题。

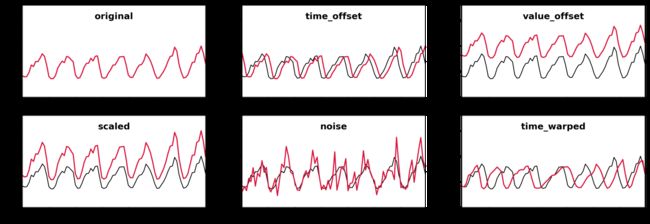
在原始数据的基础上，通过多种方法来判别几个不同情况下时间序列的相似性。

1.Euclidean and MAPE

欧氏距离指标（Euclidean distance metric）和平均绝对百分比误差（Mean Absolute Percentage Error，MAPE）。两者都是逐点计算两个时间序列的差异，这使得它们的计算速度非常快，但也限制了它们的适用性。

用Python实现如下。

import numpy as np

def calc_euclidean(actual, predic):
    return np.sqrt(np.sum((actual - predic) ** 2))

def calc_mape(actual, predic):
    return np.mean(np.abs((actual - predic) / actual))

欧氏距离指标本质上是两个时间序列（向量）之间的向量规范，因此要求两个序列的长度相等。它的值可以从0（相同的时间序列）到无穷大，实际的输出值不仅取决于两个时间序列之间的相似性，还取决于它们的长度，即比较的点数量。

MAPE也要求两个序列的长度相等，它通过逐点取距离的平均值除以实际或预测值来进行归一化。值得注意的是，这个定义不是对称的，输出是不同的，取决于哪个时间序列被认为是实际值，哪个是预测值。这可以通过用每个逐点距离除以两个时间序列的平均值来解决。

那么，它们的效果如何呢？通过观察两个时间序列之间所围成的区域（在下图中以红色标出），两种方法在具有噪音的时间序列之间表现较好，这个区域相当小，但它们在其他情况下表现相对较差。绝对值的逐点比较根本无法确定偏移或缩放的曲线是相似的，因为没有考虑到邻近点。

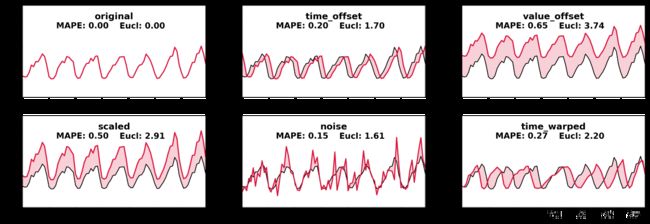
2.Pearson correlation coefficient

皮尔逊相关系数在Python中的实现方法如下。

import numpy as np

def calc_correlation(actual, predic):
    a_diff = actual - np.mean(actual)
    p_diff = predic - np.mean(predic)
    numerator = np.sum(a_diff * p_diff)
    denominator = np.sqrt(np.sum(a_diff ** 2)) * np.sqrt(np.sum(p_diff ** 2))
    return numerator / denominator

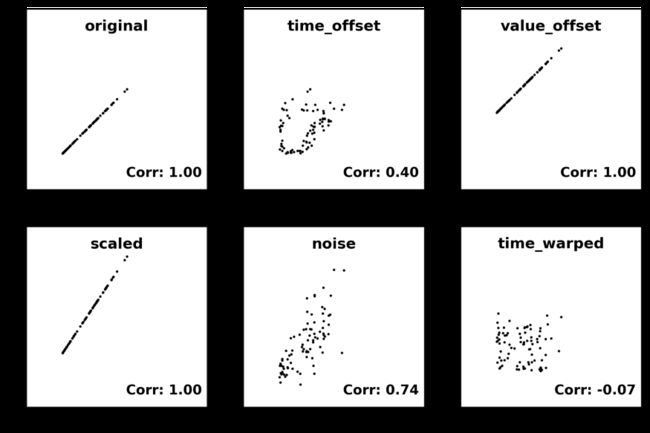
它测量两个数据集之间的线性相关性，在我们的例子中是时间序列。同样，要比较的时间序列需要有相同的长度。结果在散点图中得到较好的体现：

• 如果所有的点都形成一条上升直线，那么相关性很强，估值为1；
• 如果它们形成一条下降直线，那么这两个序列被认为是完全反相关的（行为相反），估值为-1。
• 较差的相关性表现为更分散的点云，其数值接近于0。

正如预期的那样，只要我们比较的仅是在数值维度上移动或缩放的曲线，相关性较强。添加噪音仍然会导致一个不错的相关性，但任何沿时间轴的移动都会迅速降低相关系数，因为这里和之前考虑的指标一样，只进行了逐点比较。总的来说，皮尔逊相关系数表现不错，能清楚地显示出比之前的方法更灵活。

3.Dynamic Time Warping

我们已经谈了很多关于不同时间序列之间的逐点比较是相当不灵活的，在两个稍有时间偏移的序列之间看不到很多相似之处。动态时间规整（Dynamic Time Warping，DTW）是一个解决此类问题的方法。

鲁汶大学DTAI研究小组提供了相关的开源方法（https://github.com/wannesm/dtaidistance）。DTW本质上是一种优化的方式，简单地尝试两个时间序列之间所有合理的时间映射（一个子集），并选择最佳匹配。

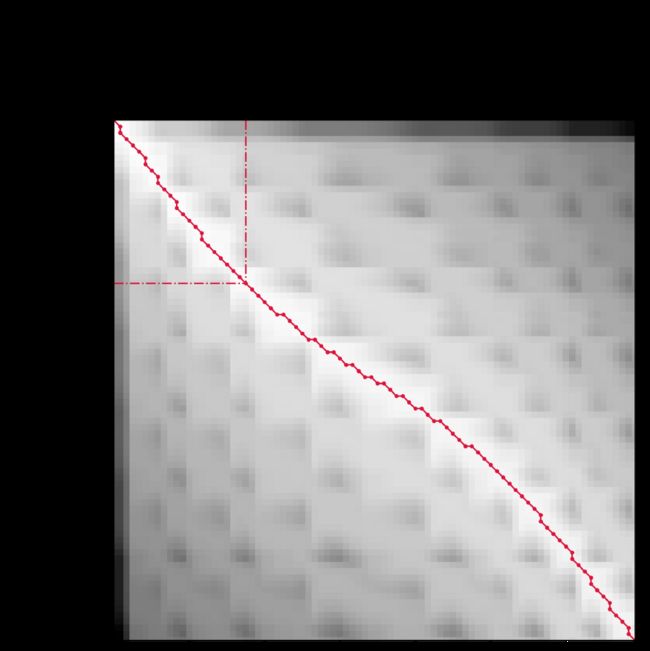
每个小方块表示两个时间序列的两个点之间的映射，深色表示映射的时间序列值之间的差异。

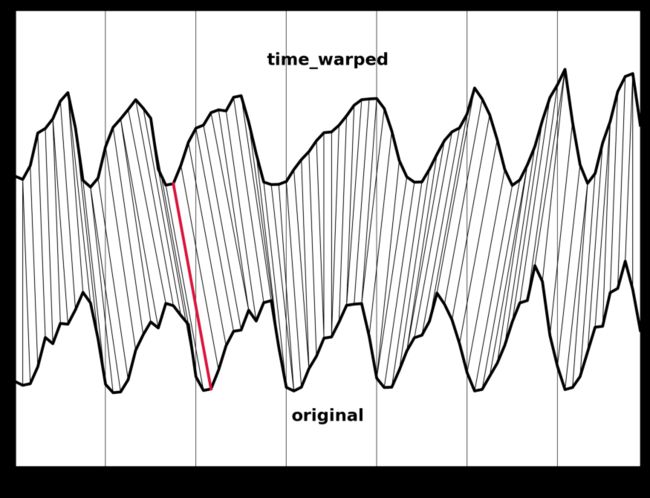
红线表示最佳匹配：该线的倾斜度和弯曲度越大，两个时间序列之间的扭曲度就越大。

绘制最佳映射图，我们可以看到两个序列之间的映射情况。

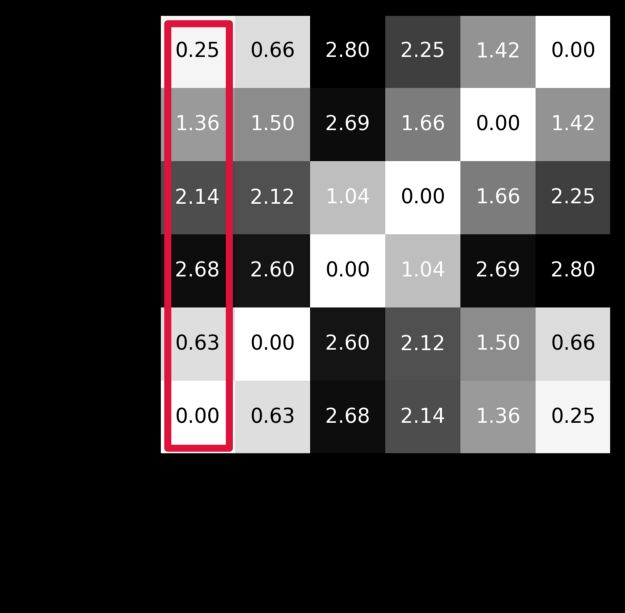
较大的数值表示较小的距离。显然，DTW能够识别类似序列的时间偏移和时间扭曲版本，但如果在数值维度上有任何偏移，它就会失效并返回较大的距离——毕竟理想扭曲路径的确定完全取决于绝对时间序列值。

4.Compression-based dissimilarity

前面提到的几种方法有一个缺点：计算量大。DTW在一定程度上降低了复杂性，但在长时间序列上执行仍然非常慢。接下来介绍的方法将具有一定的优势：基于压缩的异质性（Compression-based dissimilarity，CBD）。典型的压缩算法非常善于在任何数据中识别重复的模式，类似的时间序列同样应该包含很多类似的模式。

举个例子，假设我们要压缩的字符串是the gorilla is the king of the utility jungle, because the gorilla is data-driven。显然，the gorilla is的字符模式是一个反复出现的主题，将其存入字典，并将其出现的所有地方用一个键替换。令the gorilla is = 1，则原句变为1 the king of the utility jungle, because 1 data-driven。

这样，字符串的长度从81个字符降至72个字符，压缩率为11%。现在，如果我们有第二个完全不同的字符串，它的压缩将有一个不同的字典，将这两个字符串连接起来，然后一起压缩，与单独压缩相比，不会有任何进一步的节省。然而，如果这两个字符串是相似的，那么把它们放在一起而不是分开压缩，就可以让我们共享我们用于压缩的字典，从而进一步节省消耗。

这正是CBD的意义所在：只需比较两个时间序列单独压缩的大小和它们串联的压缩大小。这使得处理大数据变得轻而易举!

首先，我们需要对我们想要压缩的数据进行编码。如果我们直接使用时间序列值本身，几乎不会有任何共享的模式，因为即使是非常相似的时间序列也会有稍微不同的值。

尽管两个序列描述的是类似的趋势，但它们的绝对值和值差是不同的，因此大多数压缩算法不会发现任何共享模式。我们可以通过对数值进行分档并给每个分档分配一个字母来解决这个问题——这就是著名的符号聚合估计算法（Symbolic Aggregate approXimation，SAX）。

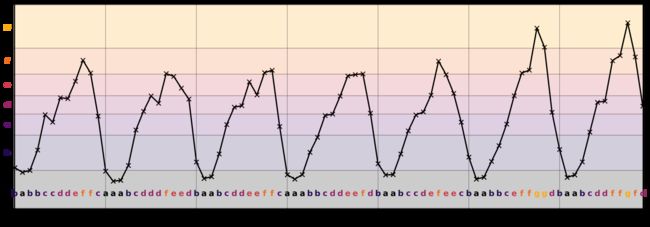
我们可以根据我们的目的选择字母表的大小（这里是7）。一个SAX和CBD的基本实现如下所示。

import bz2
import numpy as np

class CompressionBasedDissimilarity(object):

    def __init__(self, n_letters=7):
        self.bins = None
        self.n_letters = n_letters

    def set_bins(self, bins):
        self.bins = bins

    def sax_bins(self, all_values):
        bins = np.percentile(
            all_values[all_values > 0], np.linspace(0, 100, self.n_letters + 1)
        )
        bins[0] = 0
        bins[-1] = 1e1000
        return bins

    @staticmethod
    def sax_transform(all_values, bins):
        indices = np.digitize(all_values, bins) - 1
        alphabet = np.array([*("abcdefghijklmnopqrstuvwxyz"[:len(bins) - 1])])
        text = "".join(alphabet[indices])
        return str.encode(text)

    def calculate(self, m, n):
        if self.bins is None:
            m_bins = self.sax_bins(m)
            n_bins = self.sax_bins(n)
        else:
            m_bins = n_bins = self.bins
        m = self.sax_transform(m, m_bins)
        n = self.sax_transform(n, n_bins)
        len_m = len(bz2.compress(m))
        len_n = len(bz2.compress(n))
        len_combined = len(bz2.compress(m + n))
        return len_combined / (len_m + len_n)

在这段代码中，我们使用sax_bins()确定一个基于所有数值的分档，并将其设置为全局分档，以便与set_bins()一起使用，或者我们可以直接不设置分档，让它在我们调用calculate()时为每个时间序列单独计算。这两个选项之间的区别，最好的解释说明是简单地看一些示例结果（如下图所示）。同样，较大的值表示两个时间序列之间的相似性较小。

全局分档（CBD All）考虑到了绝对值。单独分档（CBD Sep）只考虑到了时间序列的形状，这样，scaled和value_offset时间序列被认为与原时间序列是非常相似的，time_offset也被确定为一个接近的时间序列。

5.Conclusion

到此，已经介绍了几种不同的判断时间序列相似度的指标，究竟哪一个效果最好呢？值得注意的是，不应该把不同的度量相互比较，因为它们赋予时间序列对的距离的绝对值只是相对于用相同度量计算的其他对的距离有意义。

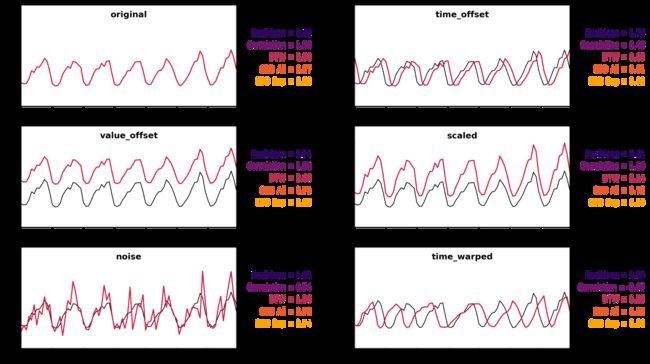
每种方法在某些特定场景下都有着不错的效果，但没有哪种方法可以做到在所有场合下是通用的。没有一个单一的衡量标准可以确定所有的这些配对都是相似的。对于一个特定的问题，哪一个是最好的，取决于在给定的背景下“相似”的定义。

在预测用电的场景下，如果它们在同一时间有高峰和低谷的话，并且这些高峰和低谷的绝对振幅对我们来说并不重要，那么我们最好选择相关系数作为相似性指标。如果振幅对两个时间序列来说都非常重要，那么最好选择欧氏或MAPE指标。这三个指标也都能比较好地处理噪声。

DTW对于寻找时间偏移或规整的曲线之间的相似性非常有针对性，但是一旦两个要比较的时间序列的绝对值有任何偏移就会失效。鉴于它在计算复杂性方面有很大的缺陷，它可能只会在明确需要处理时间规整的情况下使用。例如鸟叫声的声音分析，不同的样本可能有不同的速度，直接逐点比较并不能识别相似性或识别模式。

CBD的好处是可以轻松处理不同长度的大型时间序列。通过为所有时间序列设置SAX分档，或者为每个时间序列单独设置，我们可以选择是否考虑绝对振幅。无论哪种情况，这个指标对于量化相似性是最有用的。噪声序列和所有其他序列之间的相似性总是被判断为非常低，正如人眼所见，噪声看起来和其他地方有很大的区别。