机器学习——支持向量机SVM
一、什么是SVM
支持向量机(SVM)是一类按监督学习方式对数据进行二元分类的广义线性分类器,其决策边界是对学习样本求解的最大边距超平面,可以将问题化为一个求解凸二次规划的问题。与逻辑回归和神经网络相比,支持向量机,在学习复杂的非线性方程时提供了一种更为清晰,更加强大的方式。
具体来说就是在线性可分时,在原空间寻找两类样本的最优分类超平面。在线性不可分时,加入松弛变量并通过使用非线性映射将低维度输入空间的样本映射到高维度空间使其变为线性可分,这样就可以在该特征空间中寻找最优分类超平面。
能够画出多少条线对样本点进行区分?
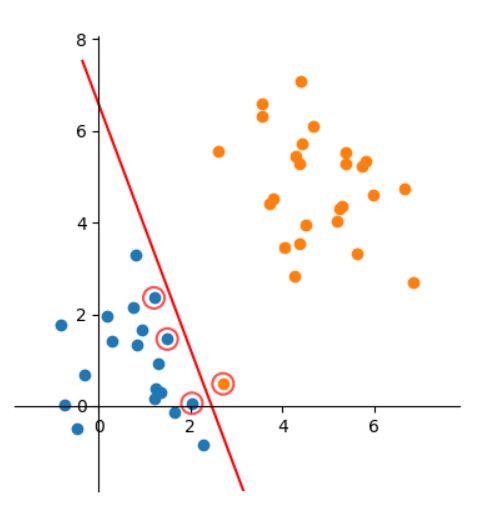
答:线是有无数条可以画的,区别就在于效果好不好,每条线都可以叫做一个划分超平面。比如上面的绿线就不好,蓝线还凑合,红线看起来就比较好。我们所希望找到的这条效果最好的线就是具有 “最大间隔的划分超平面”。
为什么要叫作“超平面”呢?
答:因为样本的特征很可能是高维的,此时样本空间的划分就不是一条线了。
画线的标准是什么?/ 什么才叫这条线的效果好?/ 哪里好?
答:SVM 将会寻找可以区分两个类别并且能使间隔(margin)最大的划分超平面。比较好的划分超平面,样本局部扰动时对它的影响最小、产生的分类结果最鲁棒、对未见示例的泛化能力最强。
间隔(margin)是什么?
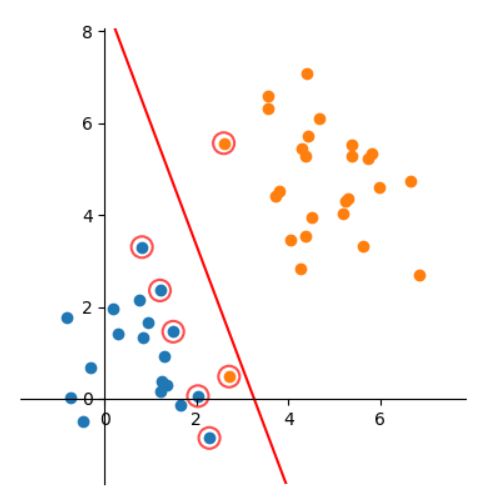
答:对于任意一个超平面,其两侧数据点都距离它有一个最小距离(垂直距离),这两个最小距离的和就是间隔。比如下图中两条虚线构成的带状区域就是 margin,虚线是由距离中央实线最近的两个点所确定出来的(也就是由支持向量决定)。但此时 margin 比较小,如果用第二种方式画,margin 明显变大也更接近我们的目标。
为什么要让 margin 尽量大?
答:因为大 margin 犯错的几率比较小,也就是更鲁棒啦。
支持向量是什么?
答:从上图可以看出,虚线上的点到划分超平面的距离都是一样的,实际上只有这几个点共同确定了超平面的位置,因此被称作 “支持向量(support vectors)”,“支持向量机” 也是由此来的。
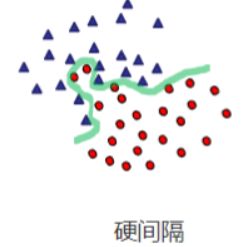
二、硬间隔
三、软间隔
软间隔能提升模型鲁棒性
四、核函数Kernel
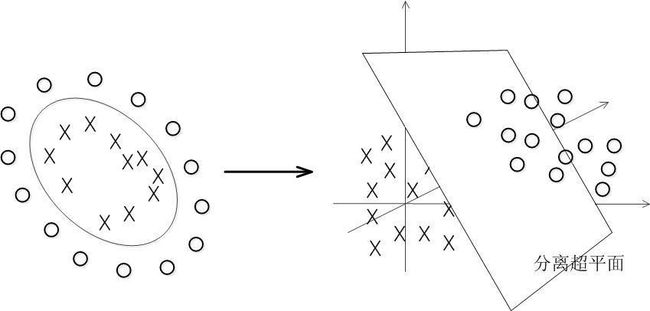
从二维不可分到高维可分
具体来说,在线性不可分的情况下,支持向量机首先在低维空间中完成计算,然后通过核函数将输入空间映射到高维特征空间,最终在高维特征空间中构造出最优分离超平面,从而把平面上本身不好分的非线性数据分开。如图所示,一堆数据在二维空间无法划分,从而映射到三维空间里划分:
五、部分参数
一般调以下几个参数:
kernel: 核,选项有’linear’ 线性核,‘poly’ 多项式核, ‘rbf’ 高斯核, 'sigmoid’等。
C: 惩罚系数,英文写的是Regularization parameter,默认值1。C越大,对错误的容忍越低,会减小与训练集的差值,但同时也会使得margin变小,泛化能力降低,会导致过拟合。反之,C越小,会适当忽略一些差值较大的点,但泛化能力较好,容易导致欠拟合。所以C太大和太小都不好。
gamma:主要用在rbf, poly和sigmoid,gamma越大,样本的接受度和影响也会下降,从而导致对错误的容忍度降低。所以当欠拟合的时候gamma应该增加。相反,小的gamma容忍度较高,适合在过拟合的时候使用。
degree:多项式核的度数。
probability: 是否采用概率估计?.默认为False
cache_size: 运行内存使用大小,默认为200M,如果设备允许可以设多一点。
shrinking:是否采用shrinking heuristic方法,默认为true
class_weight: 类别权重。
线性SVM
导入相关模块
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
from matplotlib.colors import ListedColormap数据可视化
# 载入数据
data = np.genfromtxt("../data.csv", delimiter=",")
x_data = data[:, 0:-1]
y_data = data[:, -1]
#可视化
plt.figure()
plt.scatter(x_data[:,0],x_data[:,1], c=y_data, s=30)
plt.show()利用linearsvc分类
#使用LinearSVC分类
model = LinearSVC(C=1e9)
model.fit(x_data, y_data)
print(model.coef_) # w,所有x的权值
print(model.intercept_) # b,截距
# [[0.49999991 0.49999991]]
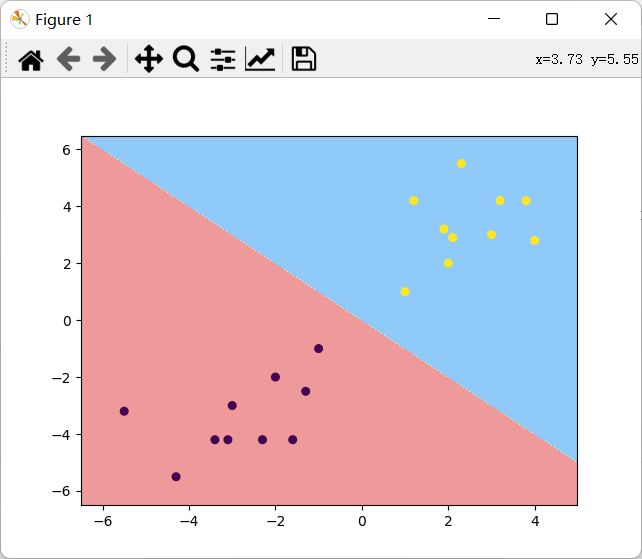
# [-1.87067246e-07]结果可视化
# 获取数据值所在的范围
x_min, x_max = x_data[:, 0].min() - 1, x_data[:, 0].max() + 1
y_min, y_max = x_data[:, 1].min() - 1, x_data[:, 1].max() + 1
# 生成网格矩阵
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
np.arange(y_min, y_max, 0.02))
# ravel与flatten类似,多维数据转一维。flatten不会改变原始数据,ravel会改变原始数据
z = model.predict(np.c_[xx.ravel(), yy.ravel()])
z = z.reshape(xx.shape)
# 等高线图
plt.figure()
custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
plt.contourf(xx, yy, z, cmap=custom_cmap)
plt.scatter(x_data[:,0],x_data[:,1], c=y_data, s=30)
plt.show()使用sklearn自带的moon数据,数据可视化
from sklearn import datasets
moons = datasets.make_moons(noise=0.15)
X = moons[0]
y = moons[1]
plt.scatter(X[y==0,0], X[y==0, 1])
plt.scatter(X[y==1,0], X[y==1, 1])
plt.show()使用LinearSVC分类,使用pipeline封装一下
def PolynomialSVC(degree, C=1.0):
return Pipeline([
("poly", PolynomialFeatures(degree=degree)),
("std_scaler", StandardScaler()),
("linearSVC", LinearSVC(C=C))
])
poly_svc = PolynomialSVC(degree=3)
poly_svc.fit(x, y)
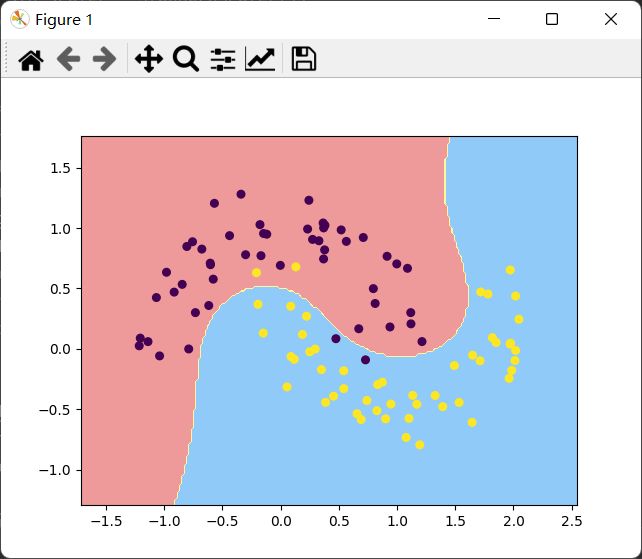
poly_svc.predict(x)多项式核函数
def PolynomialSVC(degree, C=1):
return Pipeline([
("poly", PolynomialFeatures(degree=degree)),
("std_scaler", StandardScaler()),
("linearSVC", SVC(kernel="poly", C=C,degree=degree))
])
poly_svc = PolynomialSVC(3)
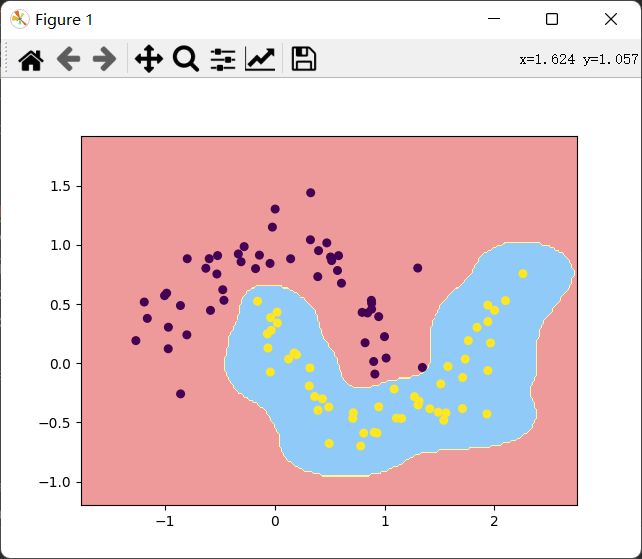
poly_svc.fit(x,y)高斯核函数
def SVC_(kernel="rbf", gamma=1):
return Pipeline([
("std_scaler", StandardScaler()),
("linearSVC", SVC(kernel="rbf", gamma=gamma))
])
svc = SVC_(kernel="rbf", gamma=10)
svc.fit(x, y)