时间序列可预测性度量

时间序列可预测性度量

关于时间序列是否可预测性的问题，之前零碎的思考过，现结合过往的项目经验，整理如下，抛砖引玉。先从简单易理解的入手。是否容易预测，不是能否预测的问题，而是是否可以精确预测。精确一词，用业界最常用的MAPE度量：

$$MAPE=\frac{100\%}{n}\sum _{i=1}^n\left|\frac{{\hat{y}}_i-y_i}{y_i}\right|$$

1.序列长度

针对时序数据，一般首先会关注序列的长度$n$，较短序列意味着数据的潜在可变性无法判断，随机成分较大，无法通过该序列历史数据揭示出规律性。从理论角度来说，样本的数量要比预测模型中参数个数更多。从经典时间序列分解理论出发，序列短则无法准确的推断其趋势、季节波动，对ARIMA等模型，将导致其自相关系数，平稳性检验等变得相对不可靠，机器学习模型，同样需要较大的样本量来避免过拟合风险。针对短序列，应该选择使用需要参数更少更简单的模型，比如移动平均，规则模型，线性回归，同时减低模型复杂。如果待预测问题属于一个较大粒度，比如门店-月销售额的短序列预测，相比较在门店-天-sku预测上更容易预测，因为潜在可变性较小，样本量(序列长度)问题相对没有那么突出。
$$n=[t_1,t_2,t_3,...,t_n]$$

2.缺失值占比

一个完整的序列，缺失值为0，由于某些因素，缺失了若干时间点的数据，就需要补全缺失值。时序数据对数据出现的位置敏感，常规的均值/众数填充不合适，这会掩盖乃至打乱数据本身的周期规律，常见的方式比如，用缺失值附近的序列值进行填充，使用前/后一位，前n+后n的平均值，或者如果知道序列的周期性，可以使用序列的上一个周期值。

填补的数据只是尽量还原数据原始的面貌，并不能完全代替真实情况，所以如果存在缺失值，即使序列数据已经补全，也有一定的失真，且更严重的是，如果缺失的值比较多，需要填充更多的值，相比较完整的序列，自然更加不好预测。

上面提到了如果缺失值很多的情况下，再去补全序列值，往往并不可行，此时需要区分缺失值是否是由于该时间点没有发生值导致的，比如在零售领域某些sku在很多天没有销售记录，也就是销售记录多天为0，此时有专门针对这种间断需求（Intermittent demand）的预测方法–Croston’s method。
$$\begin{gathered} MissingRatio=\frac{n}{1+max(T_i)-min(T_i)} \\ {T}_i:销售时间,n:序列长度 \end{gathered}$$

使用Spark.SQL直接计算代码如下：

--序列缺失率
count(dt)/(floor(datediff(max(dt), min(dt)))+1) as sale_ratio

3.变异系数(cv)

严格来讲，在时间序列领域有专门衡量序列是否平稳的度量方式，下面会讲到。按照MAE度量是否容易预测，波动性大的序列，即使有周期性，在某些时刻，由于其真实值很小（接近0），预测值略有波动就会导致MPAE剧烈上升。更重要的是波动大的序列除了是季节性本身的原因以外，很有可能还包含了未知残差。
$$\begin{gathered} \bar{x}=\frac{{\sum }_{i=1}^n{x}_i}{n} \\ S=\sqrt{\frac{{\sum }_{i=1}^n{\left(x_i-\bar{x}\right)}^2}{n-1}} \\ C.V=\frac{S}{\bar{x}}\times 100\% \\ \bar{x}:均值,S:标准差 \end{gathered}$$

所以在多条序列考察预测准确率的时候，变异系数大的序列，预测的准确率往往会下降。

--序列变异系数
stddev_samp(qty)/avg(qty) as cv_coef

以上三种是比较容易理解的方式，同时也没有考虑序列的前后的关系和季节周期性，算是一种通用的描述方式。
下面正式介绍几种针对序列是否可预测性的度量指标

4.平稳性

在ARMA/ARIMA这样的自回归模型中，前提条件是序列平稳，因此，需要对数据或者数据的n阶差分进行平稳检验，而一种常见的方法就是ADF检验，即单位根检验，判定其生成过程是否会随时间而变化。

平稳性分为强平稳和弱平稳。
强平稳的要求非常严格，它要求两组数据之间的统计性质不会随着时间改变。其要求过于严苛，理论上很难证明、实际中难以检验，所以实际弱平稳会用到的多。

它有三个要求：
$$\begin{gathered} E(Yt)=\mu \\ Var(Yt)=E((Yt-\mu ){)}^2={\sigma }^2 \\ \mathrm{Cov}\left(Y_t,Y_{t+k}\right)=E\left[\left(Y_t-\mu \right)\left(Y_{t+k}-\mu \right)\right]={\gamma }_k \end{gathered}$$
也就是

（1）随机变量的期望(均值)μ不随时间t改变；

（2）任意时刻二阶矩都存在；

（3）两个随机变量之间的自相关系数，只与这两个变量的时间间隔有关，而不随时间的推移而改变。

代码如下：

from statsmodels.tsa.stattools import adfuller
def adfuller_func(df):
    df.sort_values(by=['date'],ascending=[True],inplace=True)
    adfuller_result=adfuller(df['qty'],autolag='AIC')
    is_adfuller=None
    if adfuller_result[1]<0.05:
        is_adfuller=1
    else:
        is_adfuller=0
    result=pd.DataFrame({'store_id':df['store_id'].iloc[0],'is_adfuller':[is_adfuller]})
    return result
    

只所以这样写，是考虑到如有大规模的序列需要检测，比如100万条序列，就需要动用Spark，后面也会给出使用Spark进行操作的代码。刚也说明了在时序领域变异系数为何不是更好描述时序波动性的指标，因为季节性周期的存在，有趋势和季节波动是正常，要考虑的是一段时间内序列是否具有平稳性，而不是针对时间序列数据点的离散程度。

5.周期性

不是所有的时序数据都具备明显的周期性，如果存在周期，则在分析建模的时需加入周期性这一特性。常用的周期性函数通过正弦和余弦的函数来表示，假设f(x)是以$2\pi$为周期的函数，那么傅里叶级数为：
$$\begin{gathered} s(t)=\sum _{n=1}^N\left(a_n\cos \left(\frac{2\pi nt}{P}\right)+b_n\sin \left(\frac{2\pi nt}{P}\right)\right) \\ 年:p=365,n=10 \\ 月:p=30,n=5 \\ 周:p=7,n=3 \end{gathered}$$

import numpy as np 
import matplotlib.pyplot as plt
import scipy.signal as signal

x=np.array(df_v1['qty'])
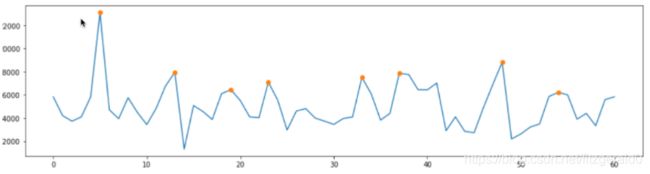
plt.figure(figsize=(16,4))
plt.plot(np.arange(len(x)),x)
plt.plot(signal.argrelextrema(x,np.greater,order=3)[0],x[signal.argrelextrema(x, np.greater,order=3)],'o')
plt.show()

也可以使用基于n阶自相关系数的方式来检测，自相关（Autocorrelation）用于评估时序数据是否依赖于其过去的数据。$Yt$与$Yt+h$之间的相关系数记为自相关系数$\rho (h)$,其函数称为自相关函数(Autocorrelation Function, ACF)通过计算序列$[t_1,t_2,t_3,t_4,...,t_n]$的$[1,2,3,...n-1]$次ACF自相关，其n-1个自相关系数排列的局部最值点的最小公倍数，可以作为周期性,如最小公倍数为7，30，12，则说明存在周，月，年的周期性。如，n-1个自相关局部最值为[7,14,21,28]，则可以认为其周期长度为7，在实际工作中数据本身的特点，周末销售高峰，原本周期性应该是7，本该是礼拜天出现的销售最高值，在某些时候可能是礼拜六，或者在这批序列中跨越了节假日这些不寻常的情况，出现的局部最大自相关系数的下标可能是[ 7, 13, 21, 28, 32]，故实践中，如只要有一个下标能被周期7整除，则判断为存在周这种周期性，具体代码细节如下。

import scipy.signal as signal
from statsmodels.tsa.stattools import acf
def cycle_test(df,order=3):
    acf_values=acf(df['qty'],nlags=df.shape[0]-1)
    max_index=signal.argrelextrema(acf_values,comparator=np.greater,order=order)#【1】
    is_cycle=['is_cycle' for i in max_index[0] if i%(2*order+1)==0][0]
    return is_cycle
    

注：

[1]signal.argrelextrema求n个自相关系数之间的局部最大值下标

[2] i%(2*order+1)，是个人在使用具有星期这种周期性的序列的设定，也就是，如果局部最大值的下标为

[ 7, 14, 21, 28, 32]

所以绘图：

ax = plt.gca()
miloc = plt.MultipleLocator(7)
ax.xaxis.set_minor_locator(miloc)
ax.grid(axis='x', which='minor')
plt.plot(np.arange(len(acf_values)),acf_values)
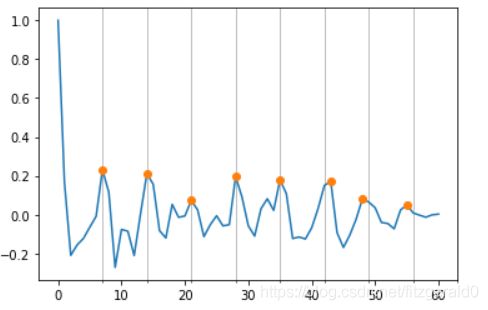
plt.plot(signal.argrelextrema(acf_values,comparator=np.greater,order=3)[0],acf_values[signal.argrelextrema(acf_values, np.greater,order=3)],'o')

用自相关系数做图，如上，我们可以看到在能被7整除的几个点都是局部极值点，特意用间隔为7的网格和点都标注在图上。

6.复杂性

序列数据中潜在规律成分多少可以通过计算序列复杂度来度量，复杂度越低，时序内部的有序成分越多，也更具规律性。了解序列本身蕴含的稳定或者波动性，也便于解释某些商品预测为何比其他商品预测准确性更差。近年来有不少学者提出可以使用排列熵(Permutation Entropy)针对时间序列本身具有的空间信号特性进行检验，该方法计算简单，抗噪声能力强，对时间敏感度高，输出结果直观，应用范围广泛。理论方面论文和详细推导可以参考《Practical considerations of permutation entropy: A tutorial review》与《排列熵算法的应用与发展》。
先给出代码角度进行拆解，如果无意深入代码和公式的细节把握，也有一个开源的python库，该库还有其他熵的计算方法（比如Sample Entropy ，Multiscale Entropy），链接：https://github.com/nikdon/pyEntropy

pip install pyentrp

如果是仅仅使用排序熵，那么该库中的这两个函数就可以完成。

from math import factorial
import numpy as np
def _embed(x, order=3, delay=1):
    N = len(x)
    Y = np.empty((order, N - (order - 1) * delay))
    for i in range(order):
        Y[i] = x[i * delay:i * delay + Y.shape[1]]
    return Y.T

def permutation_entropy(time_series, order=3, delay=1, normalize=False):
    x = np.array(time_series)
    hashmult = np.power(order, np.arange(order))
    # Embed x and sort the order of permutations
    sorted_idx = _embed(x, order=order, delay=delay).argsort(kind='quicksort')#【1】
    # Associate unique integer to each permutations
    hashval = (np.multiply(sorted_idx, hashmult)).sum(1)
    # Return the counts
    _, c = np.unique(hashval, return_counts=True)#【2】
    # Use np.true_divide for Python 2 compatibility
    p = np.true_divide(c, c.sum())
    pe = -np.multiply(p, np.log2(p)).sum()#【3】
    if normalize:
        pe /= np.log2(factorial(order))
    return pe

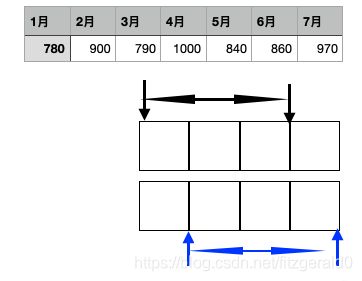
函数_embed中order为窗口大小，delay为移动大小，如下图，在一条序列上三条（窗口）数据每次移动一个单位。

​

注：

[1]对重构矩阵的中的每一个窗口list进行排序，如下图左，下图右为相应的幕，如果取滑动窗口为0，那就是(1,3,9)，右边矩阵可以看作是权值矩阵，两个矩阵相乘，求和

[2] 求和后每个窗口值出现的频率；

[3] 对频率求熵。

当然排序熵也是一种绝对度量方式，在面对多个序列的时候，更大的表明序列更加复杂，依据很多资料都表明，在序列够长且没有明显的周期性这种复杂度更高的模型上，深度学习模型是一种值得尝试的模型。

总结

所以以上六种方法和思路也是在面对总众多大规模时间序列时，依据序列本身的数据特性的不同，选择其更合理模型和参数用于建模。

因为是聚焦在是否可预测性，所以只写了以上几种针对序列统计特征的描述，比如序列是否正态分布的检验，随机性，线形与非线形检验等在此也就不多着墨。因为是面向百万的序列进行操作，所以给出一个针对平稳性，周期性，复杂度计算的spark的panda_udf分组计算Grouped map的小demo。代码请点击