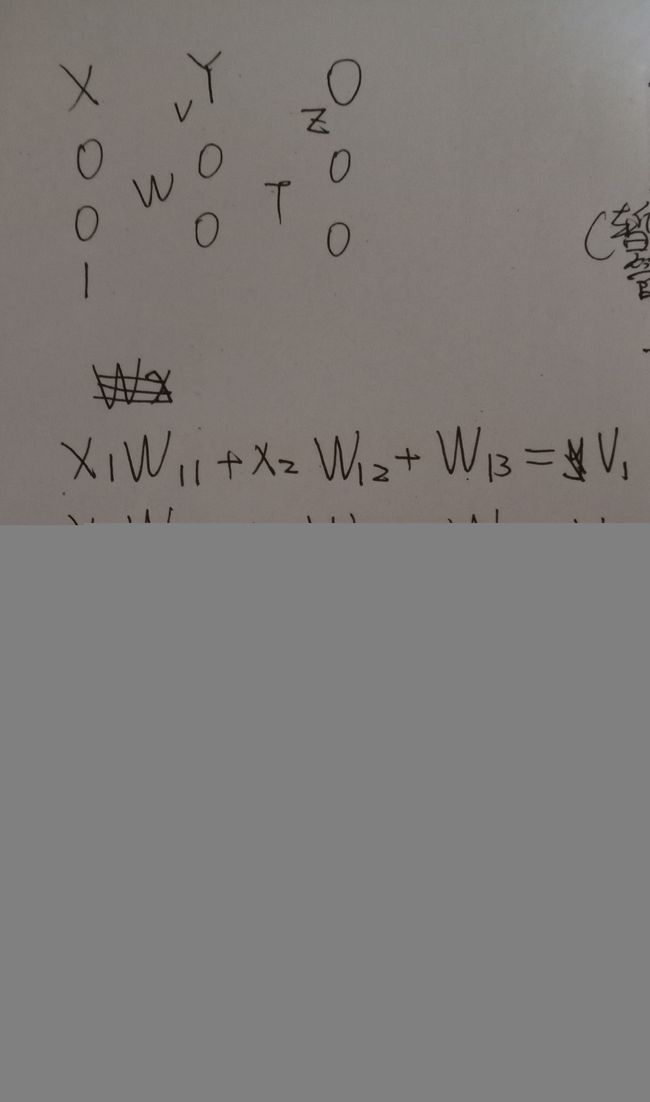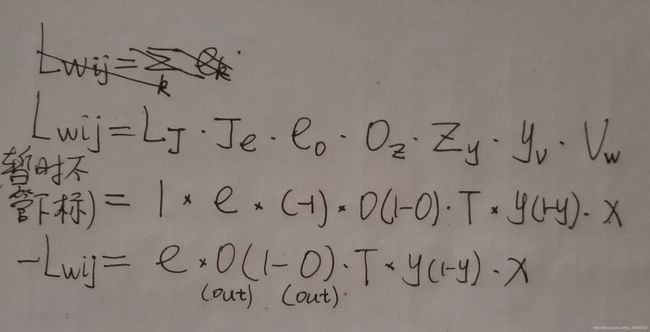从数学上推导神经网络BP算法(向后传播)的矩阵形式————思考记录
这篇文章不适合初学者看,而适合对BP算法中矩阵形式抱有疑惑的人看;读者应该具有矩阵的基本知识,BP算法的基本知识,matlab的基本矩阵操作。
最近被BP算法整得头大,今天终于想通,记录一下我的想法,主要是理解它为什么要这么算。
BP算法主要使用的权值更新方法就是梯度下降算法,先求对权值的导数(图太大,放在下面):
解释:
左上角是神经网络示意图,X为输入,其中X3==1.W和T分别为第一层和第二层权值。v为权值和(v11=x1*w11+x2*w12+w13,以此类推),Y为隐层节点,y=sigmoid(v)(sigmoid是一种激活函数),z为权值和(z11=y1*t11+y2*t12,以此类推),O为输出,O=sigmoid(z).
误差ek=d-yk(d,训练样本中输入数据对应的输出数据);代价函数L:表明当前输出和正确输出的偏差值,L越小,模型越精准(如果你疑惑为什么不用ek衡量偏差:显然L恒大于零,比ek更优秀);
Jk,对于每一个输出节点都有一个Jk,Jk求和,就是我们的代价函数。
dW:隐层权值的更新量。![]() :学习步长。
:学习步长。
输出层计算出的误差,向后传播可以计算隐层误差,从而更新隐层权值。我们在对上面对导数的推导中,知道取负梯度的方向,函数下降最快,代价函数J值就会减少。
注意左上角x,y下面的是圆圈,表示待定;y右边的那个是O,英文为out。
这是我的老师的ppt代码,使用的是matlab,主要难点就是理解W2',理解计算过程。
即正确的BP算法更新隐层权值的矩阵形式应该是:dW1=![]() *delta1*x'
*delta1*x'
简单解释一下:
dW1:隐层权值的更新值。![]() :学习步长。delta1是一种中间变量,delta1=y1.*(1-y1).*e1,相当于我的d1,y1就是隐层输出,相当于我的y。e1=W2'*delta,W2是第二层的权值,相当于我的T;delta相当于我的d2;
:学习步长。delta1是一种中间变量,delta1=y1.*(1-y1).*e1,相当于我的d1,y1就是隐层输出,相当于我的y。e1=W2'*delta,W2是第二层的权值,相当于我的T;delta相当于我的d2;
没看懂是吧?哈哈,BP求导数形式容易看懂,矩阵形式不易看懂,以下从导数形式推导出矩阵形式。
我的想法如下图:(图太大,放在下面)
解释:
左上角是神经网络示意图,X为输入,其中X3==1.W和T分别为第一层和第二层权值。v为权值和(v11=x1*w11+x2*w12+w13,以此类推),Y为隐层节点,y=sigmoid(v)(sigmoid是一种激活函数),z为权值和(z11=y1*t11+y2*t12,以此类推),O为输出,O=sigmoid(z).
误差ek=d-yk(d,训练样本中输入数据对应的输出数据);代价函数L:表明当前输出和正确输出的偏差值,L越小,模型越精准(如果你疑惑为什么不用ek衡量偏差:显然L恒大于零,比ek更优秀);
Jk,对于每一个输出节点都有一个Jk,Jk求和,就是我们的代价函数。
dW:隐层权值的更新量。![]() :学习步长。
:学习步长。
输出层计算出的误差,向后传播可以计算隐层误差,从而更新隐层权值。我们在对上面对导数的推导中,知道取负梯度的方向,函数下降最快,代价函数J值就会减少。
注意左上角x,y下面的是圆圈,表示待定;y右边的那个是O,英文为out。
我在存储时,对于每一组数据,把每一层节点存储为列向量,这样可以直接计算,减少矩形转置;当数据组数要增加时,直接增加列向量即可。
对于多组数据,用到分块矩阵的知识,将矩阵列分块,每一列都是一组数据,这样不会混淆。
注意这里的两种看法:比如Tki,当k,i为范围内任意值时,Tki代表T里第k行第i列的一个元素;当k,i为T行数和列数时,T表示矩阵。
同理对于第二层到第三层是一个单层神经网络,其权值更新为:steplen*e(jm)*o(jm)*(1-ojm)*y(im),同样将每组数据(列向量提取出来)对T更新。
更新:d1*T'*d2——>d1点乘(T转置*d2)