深度学习： 梯度下降是如何实现的？

写在最前面的话

大多数深度学习算法都涉及某种形式的优化。写这个系列博客的目的也是为了整理这些相关的优化方法。对于之前会的，可以在这里加深了解一下，对于之前没有听说过的，这里就当认识一下了。老规矩，我不生产知识，我只是尽量把知识摆放的姿势优美一些。。。

优化的概念
什么是优化呢？优化就是指改变$x$，使得某个函数$f(x)$的结果最大化或者最小化。通常我们以最小化$f(x)$指代大多数最优化问题。那么最大化就可以通过由最小化算法最小化$-f(x)$来实现。是不是有点拗口？换成人话就是：
1，我们最小化这个函数$f(x)$
2，我们得到这个函数的负数$-f(x)$
3，我们最小化这个函数。
注意上面提到的函数$f(x)$在深度学习中通常就是指代损失函数。

一些基本概念
我们把要最小化或者最大化的函数称为目标函数或者准则。当我们对其进行最小化时，也把他称为代价函数、损失函数或误差函数。关于损失函数的内容，大家可以关注我的博文啥也不懂照样看懂交叉熵损失函数。

我们通常使用一个上标*表示最小化或者最大化的$x$值，例如$x^{\ast }=argminf(x)$.

现在我们简单回顾一下微积分的相关概念。
假设有一个函数$y=f(x)$，其中$x$和$y$都是实数。这个函数的导数记为$f^{{}^{\prime }}(x)$或者$\frac{dy}{dx}$。导数$f^{{}^{\prime }}(x)$代表$f(x)$在点$x$处的斜率。换句话说就是他表明如何缩放输入的小变化才能在输出获得相应的变化：$f(x+ϵ)\approx f(x)+ϵf^{{}^{\prime }}(x)$。

因此导数对于最小化一个函数很有用，因为他告诉我们如何更改$x$来略微的改善$y$。例如，我们知道对于足够小的$ϵ$来说，$f(x-ϵsign(f^{{}^{\prime }}(x)))$比$f(x)$小。
这里简单的说一下推导过程吧：
1，假设$f^{{}^{\prime }}(x)$大于0，
2，则$f(x)$是一个增函数
3，则它的正弦函数$sign(f^{{}^{\prime }}(x)$大于0，
4，则$x-ϵsign(f^{{}^{\prime }}(x))$小于$x$，
5，则$f(x-ϵsign(f^{{}^{\prime }}(x)))$比$f(x)$小。

对于$f^{{}^{\prime }}(x)$小于0的情况是一样的。

我们将$x$往导数的反方向移动一小步来减少$f(x)$。这种技术称为梯度下降。下图展示的是一个例子。

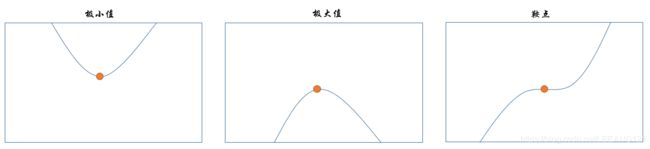
局部极值的概念
当导数为0时，无法提供往哪个方向移动的信息。因此导数为0的点我们称为临界点或者驻点。一个局部最小值意味着这个点的$f(x)$小于所有的临近点，因此不可能通过移动无穷小的步长来减小$f(x)$。一个局部极大值意味着这个点的$f(x)$大于所有的临近点，同样不可以通过移动无穷小的步长再次增大。但是有些临界点既不是最小点也不是最大点，我们称之为鞍点。如下图所示

全局极值的概念
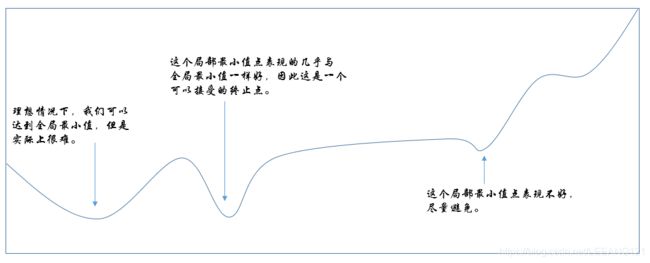
使$f(x)$取得绝对的最小值（相对所有其他值）的点是全局最小点。函数可能只有一个全局最小点或者存在多个全局最小点，还可能存在不是全局最优的局部最小点。在深度学习的背景下，我们要优化的函数可能含有许多不是最优的局部最小点，或者还有很多处于非常平坦的区域内的鞍点。尤其当输入是多维的时候，所有这些都将使优化变得困难。因此我们通常寻找是$f$非常小的点，但是在任何形式意义下并不一定是最小，如下图所示：

我们经常最小化具有多维输入的函数：$f:R^n\to R$.为了使‘最小化’的概念有意义，输出必须是一维的（标量）。

针对具有多维输入的函数，我们需要用到偏导数的概念。偏导数$\frac{\partial }{\partial x_i}f(x)$衡量点$x$处只有$x_i$增加时，$f(x)$如何变化。梯度是相对一个向量求导的导数：$f$的梯度是包括所有偏导数的向量，记为${\forall }_{x}f(x)$。梯度的第$i$个元素是$f$关于$x_i$的偏导数。在多维情况下，临界点是梯度中所有元素都为零的点。

在$u$（单位向量）方向的方向导数是函数$f$在$u$方向的斜率.换句话说，方向导数是函数$f(x+\alpha u)$关于$\alpha$的导数（在$\alpha =0$时取得）。使用链式法则，我们可以看到当$\alpha =0$时，$\frac{\partial }{\partial \alpha }f(x+\alpha u)=u^T{▽}_{x}f(x)$

为了最小化$f$，我们希望找到使$f$下降的最快的方向。计算方向导数：
$\underset{u,u^{T}u=1}{\min }{u}^T{▽}_{x}f(x)=\underset{u,u^{T}u=1}{\min }{\Vert u\Vert }_2{\Vert {▽}_{x}f(x)\Vert }_{2}cos\theta$

其中$\theta$是$u$与梯度的夹角。将${\Vert u\Vert }_2=1$带入，忽略与$u$无关的项，就能简化得到$\underset{u}{\min }cos\theta$。 这在$u$与梯度方向相反时取得最小。换句话说，梯度向量指向上坡，负梯度向量指向下坡。我们在负梯度方向是移动可以减少$f$。这被称为最速下降法或者梯度下降。

参数更新
最速下降更新参数的函数：
$x^{{}^{\prime }}=x-\epsilon {▽}_{x}f(x)$
其中$\epsilon$为学习率。是一个确定步长大小的正标量。我们可以通过几种不同的方法来选择$\epsilon$。普遍的方式是选择一个小常数。有时候我们通过计算，选择使方向导数消失的步长。

最后
本文参考自深度学习