GAMES101-现代计算机图形学学习笔记(作业04)
GAMES101-现代计算机图形学学习笔记(作业04)
Assignment 04
-
- GAMES101-现代计算机图形学学习笔记(作业04)
- 作业
-
- 作业描述
- 思路
原课程视频链接以及官网
b站视频链接: link.
课程官网链接: link.
作业
作业描述
B e ˊ z i e r Bézier Beˊzier 曲线是一种用于计算机图形学的参数曲线。在本次作业中,你需要实
现 d e C a s t e l j a u de Casteljau deCasteljau 算法来绘制由 4 个控制点表示的 Bézier 曲线 (当你正确实现该
算法时,你可以支持绘制由更多点来控制的 B e ˊ z i e r Bézier Beˊzier 曲线)。
而在本次实验中,你需要完成的任务是:
1. bezier:该函数实现绘制 B e ˊ z i e r Bézier Beˊzier 曲线的功能。它使用一个控制点序列和一个 OpenCV::Mat 对象作为输入,没有返回值。它会使 t 在 0 到 1 的范围内进 行迭代,并在每次迭代中使 t 增加一个微小值。对于每个需要计算的 t,将调用另一个函数 recursive_bezier,然后该函数将返回在 B e ˊ z i e r Bézier Beˊzier 曲线上 t 处的点。最后,将返回的点绘制在 OpenCV::Mat 对象上。
2. recursive_bezier:该函数使用一个控制点序列和一个浮点数 t 作为输入,实现 d e C a s t e l j a u de Casteljau deCasteljau 算法来返回 B e ˊ z i e r Bézier Beˊzier 曲线上对应点的坐标。
3. 实现对 B e ˊ z i e r Bézier Beˊzier 曲线的反走样
思路
① bezier 函数
该函数实现了 t 在 [0,1] 范围内的递增,并且每次递增都通过调用 recursive_bezier 函数得到了曲线中新增的点,实现如下:
void bezier(const std::vector<cv::Point2f> &control_points, cv::Mat &window)
{
for (double t = 0.0; t <= 1.0; t += 0.001)
{
auto point = recursive_bezier(control_points, t);
window.at<cv::Vec3b>(point.y, point.x)[1] = 255;
}
}
② recursive_bezier 函数
该函数实现 d e C a s t e l j a u de Casteljau deCasteljau 算法获取每次 t 对应的点的坐标,该算法的步骤如下:
- 考虑一个 p 0 , p 1 , . . . , p n p0 , p1 , ... ,pn p0,p1,...,pn 为控制点序列的 B e ˊ z i e r Bézier Beˊzier 曲线。首先,将相邻的点连接
起来以形成线段。 - 用 t : (1 − t) 的比例细分每个线段,并找到该分割点。
- 得到的分割点作为新的控制点序列,新序列的长度会减少一。
- 如果序列只包含一个点,则返回该点并终止。否则,使用新的控制点序列并
转到步骤 1。
实现如下:
cv::Point2f recursive_bezier(const std::vector<cv::Point2f> &control_points, float t)
{
std::vector<cv::Point2f> points = control_points;
// 当序列大于三个点时会继续迭代
while (points.size() >= 3)
{
std::vector<cv::Point2f> points_temp;
// 找到每个点按 t : (1 − t) 比例划分的新的顶点
for (int i = 0; i < points.size() - 1; i++)
{
cv::Point2f first = points[i];
cv::Point2f second = points[i + 1];
cv::Point2f mid = (1 - t) * first + t * second;
points_temp.push_back(mid);
}
points = points_temp;
}
// 序列小于三个点时,此时序列中只有两个点,连接两点,按 t : (1 − t) 取中点,那么该中点就为结束点
cv::Point2f start = points[0];
cv::Point2f end = points[points.size() - 1];
cv::Point2f mid = (1 - t) * start + t * end;
return mid;
}
③ B e ˊ z i e r Bézier Beˊzier 曲线的反走样:
课程中的描述为:对于一个曲线上的点,不只把它对应于一个像素,你需要根据到像素中心的距离来考虑与它相邻的像素的颜色。
这里我实现了 4XMSAA的反走样,个人理解如下:

假设 P ( x , y ) P(x,y) P(x,y) 表示红点, 那么其相邻四个像素的位置应该由图中圆圈表示,范围为 [xmin, xmax], [ymin, ymax],分别用这四个相邻像素到红点的距离的权重以及这四个相邻像素的颜色进行加权,得到反走样的结果,公式如下:
r e s = ( ∑ w e i g h t ∗ c o l o r ) / ∑ w e i g h t res =( \sum weight * color) / \sum weight res=(∑weight∗color)/∑weight
void MSAA_4X(float x, float y, cv::Mat &window)
{
int min_x = std::max(0, static_cast<int>(floor(x)));
int max_x = std::min(window.cols - 1, static_cast<int>(ceil(x)));
int min_y = std::max(0, static_cast<int>(floor(y)));
int max_y = std::min(window.rows - 1, static_cast<int>(ceil(y)));
window.at<cv::Vec3b>(y, x)[1] = 255;
double res = 0;
double sigma = 1.0; // 高斯权重因子
double weight_total = 0;
for (int i = min_x; i <= max_x; i++)
{
for (int j = min_y; j <= max_y; j++)
{
// 邻域像素位置到红点的距离
double dist = sqrt(pow(x - i, 2) + pow(y - j, 2));
// 距离权重(高斯权重)
double weight = exp(-dist / sigma);
int colors = window.at<cv::Vec3b>(j, i)[1];
res += static_cast<double>(colors) * weight;
weight_total += weight;
}
}
res /= weight_total;
window.at<cv::Vec3b>(y, x)[1] = static_cast<int>(res);
}
void bezier(const std::vector<cv::Point2f> &control_points, cv::Mat &window)
{
for (double t = 0.0; t <= 1.0; t += 0.001)
{
auto point = recursive_bezier(control_points, t);
// window.at(point.y, point.x)[1] = 255;
// 调用4XMSAA
MSAA_4X(point.x, point.y, window);
}
}
结果:
B e ˊ z i e r Bézier Beˊzier 曲线:
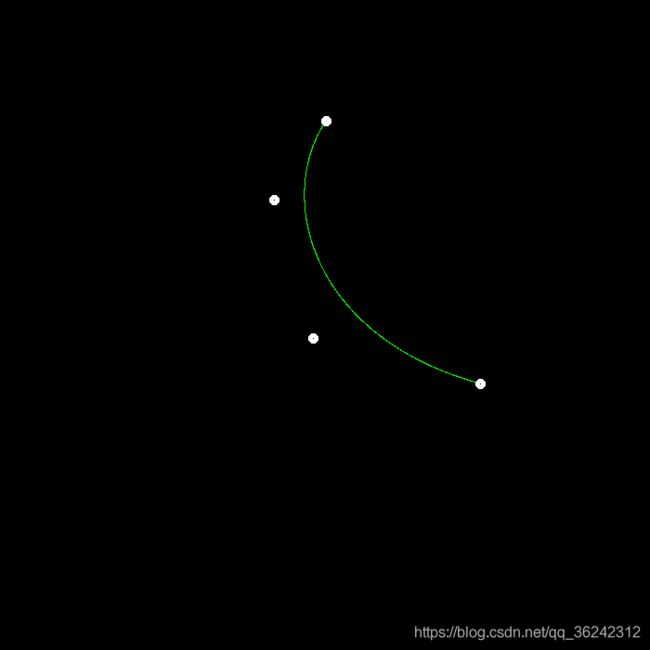
B e ˊ z i e r Bézier Beˊzier 曲线 + n a i v e B e z i e r naiveBezier naiveBezier 曲线:
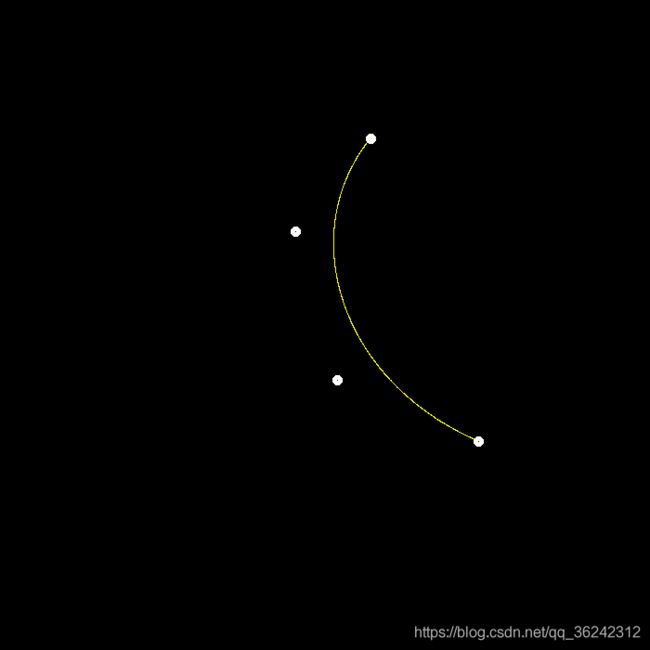
反走样后的 B e ˊ z i e r Bézier Beˊzier 曲线, 由于采用了邻域像素的加权,所有颜色有点糊:

如有问题希望指出