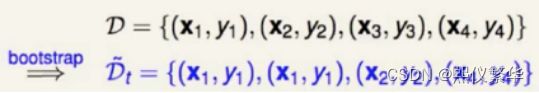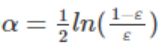机器学习算法23 决策树到集成学习思想(03 _Adaboost: 获取基础模型，错误率&权重错误率定义，计算基础模型权重α的方法 )
目录
1 什么是Adaboost
1.1 如何获得不同的g(x)
1.2 什么是数据的权重weight
1.3 权重与函数的关系
2 Adaboost中的数据权重Un
2.1 错误率&权重错误率定义
2.2 具体实现流程
3 计算α的方法
3.1 计算α的方法
3.2 adaboost 样本权重、基础模型权重计算流程
3.3 adaboost 需要弱一点的数
3.4 Adaboost 全局过程
1 什么是Adaboost
1.1 如何获得不同的g(x)
AdaBoost
- 通过赋予样本不同的权重获得不同的g(x)
- 基分类器g(x)大多使用decision-stump决策桩
- 我们通过修改数据的权重，使得本次训练的弱分类器在上次弱分类器做的不好的地方进行训练
1.2 什么是数据的权重weight
bagging中权重是什么意义?
解释：
右边的图：y≠h（x） 真实值不等于预测值，表示判错的，加和，然后除以总样本数，实际就是错误率，右边的4表示总样本数。
左边的图：带有权重的错误率（权重错误率），怎样理解这件事呢，第一条样本的权重是2，第四条样本的权重是1，如果把第一条判错和把第四条判错，性质是不一样的。（判错的样本权重加和 得到总错误率），左边的4 总样本权重加和。
1.3 权重与函数的关系
对于同一个算法
-
训练集不同，生成的模型一定不同
-
如果训练集相同, 我们调整训练集中数据的权重，生成的模型也一定不同
对于同一个模型
-
输入的数据权重不同，模型预测的正确率也一定不同
-
可以通过调整输入数据的权重，让本来还不错的分类器的正确率达到1/2（注意：这个正确率实际上是 权重错误率）
备注：Adaboost通过调整数据集的权重达到0.5来训练下一个弱分类器：
如何让第二个分类器，更关注于第一个分类器没有分好的部分？将判错的样本权重提升，将判对的样本数据权重下降，让第一个分类器对调整好的数据准确率为0.5，基于这样的数据再去训练第二个分类器。
2 Adaboost中的数据权重Un
2.1 错误率&权重错误率定义
数据预测的错误率 =（错误数据的个数）/(全部数据的个数）
数据预测的权重错误率 =（预测错误数据的权重和）/(全部数据的权重和）
举例
有一个标签集实际是{+1，+1，+1，+1，-1}
- 我们训练出一个g1(x)的分类结果{+1，+1，+1，+1，+1}
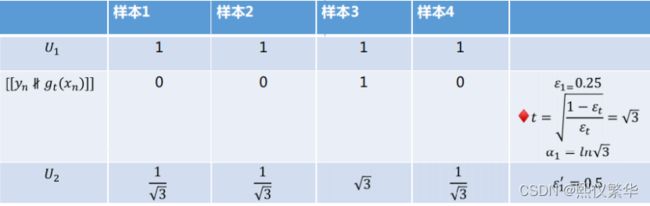
- 当所有数据的权重都为1/5时，错误率是多少？权重错误率是多少？[1/5,1/5]
- 当-1的权重是1/2, 其余+1是1/8的时候，权重错误率是多少？权重错误率=(1/2) /(1/2+4*1/8)=0.5
小结
- 在训练集的每个数据背后都标注一个权重，初始权重为1/N，此时数据错误率等于权重错误率
- 每一轮训练一个当前权重下权重错误率最低的g(x) 注：就是训练一个基础模型
- 迭代生成下一轮的权重 注：缩放权重值，带到下轮训练
- 考虑一下decision-stump，下一轮数据权重变了，训练出来的分类器内部会发生什么改变？
（个人理解：分类器会更加关注上一轮被判错的数据，致使分类器的判决条件倾向于上一轮判错的值）
2.2 具体实现流程
既然通过权重不同来训练弱分类器模型gt(x)，那么我们每次找到g(x)都应该使当前时刻权重正确率最大
目标：将当前的样本权重做调整，使其在当前模型的准确率降低，将调整权重后的样本带入下一轮模型训练。
我们想对t时刻训练错误的样本的权重进行调整，使其训练错误的样本的权重之和调整为训练正确的样本的权重之和 作为 在t+1时刻的样本权重。因为就说t+1时刻 的数据具有t时刻训练错误的样本的权重之和等于训练正确的样本的权重之和 。
上图中所述： t时刻预测不正确的权重之和为1126，预测正确的权重之和为6211，不正确的权重错误率为1126/7337,正确的权重错误率为6211/7337.
下一轮： t+1时刻预测不正确的权重之和=t时刻的 不正确的权重*预测正确的权重之和
t+1时刻预测正确的权重之和 =t时刻的 正确的权重*预测不正确的权重之和
目标：t+1时刻预测正确的权重之和=t+1时刻预测不正确的权重之和
等价于：t时刻的 不正确的权重之和*预测正确的权重之和=t时刻的 正确的权重之和*预测不正确的权重之和
等式左右两边都除以 不正确的权重之和+正确的权重之和=总权重之和
等价于：
不正确的权重之和*预测正确的权重之和 正确的权重之和*预测不正确的权重之和
—————————————————— = ——————————————————
总权重之和 总权重之和
等价于：
不正确的权重之和 *（预测正确的权重之和/总权重之和 ） =正确的权重之和(预测不正确的权重之和/ 总权重之和)
其中： 预测不正确的权重之和/ 总权重之和=不正确的权重错误率=
调整样本权重的方法如下：
在不正确的权重错误率为1126/7337 下，
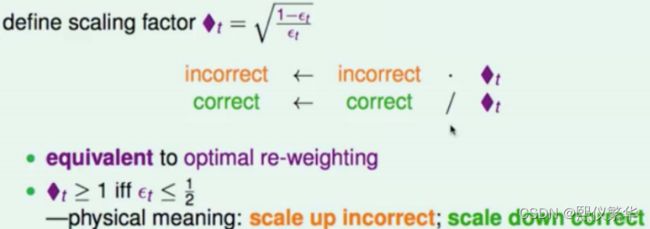
调整样本权重的方法： t时刻不正确样本的权重做（1- ）关系的调整（放大）， 正确样本的权重做 关系的调整（缩小）。
即：定义缩放系数为sqrt((1-ε)/ε），
t时刻不正确样本的权重*sqrt((1-ε)/ε） ，t时刻正确样本的权重/ sqrt((1-ε)/ε）
迭代每一轮物理权重
时的方式
设A 为正确的总权重之和 ，B为错误的总权重之和:
有 A*ε = B*(1-ε)
总权重和 C = A/(1-ε) = B/ε
上式 左乘以A*ε 右乘以 B*(1-ε) ==> A*ε*A/(1-ε) = B*(1-ε)*B/ε
上式 =A*A*ε/(1-ε) = B*B *(1-ε)/ε
上式 取 1/2 次幂==> A* sqrt(ε/(1-ε)) = B *sqrt((1-ε)/ε）
小结：
（1）使用adaboost 算法中我们需要获取不同的基础模型g（x）：
方式是：通过赋予样本不同的权重来获取不同的g（x），在给定样本的权重后我们就能计算缩放系数，知道缩放系数以后我们就知道了下一轮计算样本的权重。
（2） 集成学习还需要知道每个基础样本g（x）的权重值。
3 计算α的方法
3.1 计算α的方法
对于优秀的g(x)应该给与的权重大，（我们前面已经知道：错误率越小越优秀。也就是缩放系数越大越优秀）
也就是要找：与Δt正相关且Δt为1时候值为0的α
解释：（1）正相关：体现出与优秀成度成正比；（2）Δt为1表示 错误率为0.5 ，0.5表示瞎蒙。瞎蒙的时候表示对应 的基础模型要没有意义，也就是系数a为0
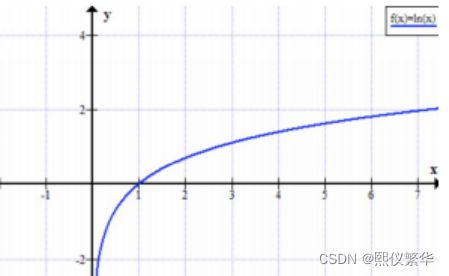
正好我们知道ln函数是递增的 并且穿过（1，0）点，
所以我们取α=ln(Δt)
即： 
3.2 adaboost 样本权重、基础模型权重计算流程
总结：我们知道样本后即可计算 -->不正确的权重错误率 -->根据sqrt((1-ε)/ε）即可计算缩放系数Δt -->根据公式α=ln(Δt) 即可计算
3.3 adaboost 需要弱一点的数
如果所有的样本是不同的，生成的是一个全量生长的树，那么准确率等于1 ，不正确的权重错误率等于0，缩放系数等于无穷大，a也就等于无穷大。a=无穷大 也就意味这 这一个基础模型独裁。
为了避免独裁或者过拟合 我们需要剪枝pruned：这里我们不适用全部的样本（行采样，和样本对应的权重正比的采样），我们使用部分样本，就能生成若一点的决策树。通常剪枝只会限制树的层数。
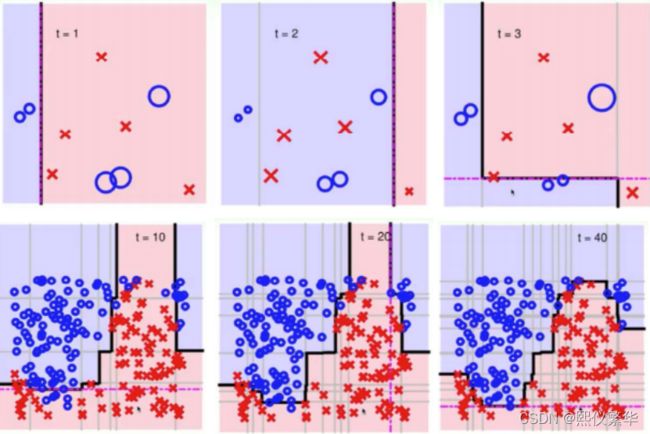
3.4 Adaboost 全局过程
每一根线都有一个权重值，最后将权重值大的连起来就是整个分类模型。