【差分隐私】Hyperparameter Tuning with Renyi Differential Privacy论文解读
【差分隐私】Hyperparameter Tuning with Renyi Differential Privacy论文解读
文章目录
- 【差分隐私】Hyperparameter Tuning with Renyi Differential Privacy论文解读
- 摘要
- 一、Introduction
-
- 1.our contributions
- 2.Background and Related Work
- 二、Motivation
- 三、Our Positive Results
-
- 1.Problem Formulation
- 2.Strawman approach: repeat the base algorithm a fixed number of times
- 3.Our algorithm for hyperparameter tuning
- 四、Main Results
- 五、Conclusion
摘要
现有的研究中,很多对于训练算法中,超参数的微调可能导致的信息泄露进行研究和推理。本文首先说明了简单地基于非私人训练运行设置超参数是如何泄露私人信息的。基于这一观察结果,我们随后在Renyi差分隐私框架内为超参数搜索过程提供隐私保障。
一、Introduction
许多机器学习任务中,训练数据可能包含敏感的隐私信息。而差分隐私为其提供了强大的隐私保证。其中,DP-SGD是噪声梯度下降中的流行方法。它与标准的梯度下降有三个不同之处:1)是梯度下降是在选取的lots上,对每个样本计算梯度2)梯度裁剪也是在每个样本上进行裁剪 3)噪声是在lots上的平均梯度上进行添加。在机器学习过程中,会引入超参数。训练过程中,会对超参数设置重复多次,以进行调优。我们也需要考虑,在训练过程重复是,超参数的调优是否会泄露私人信息
1.our contributions
(1)我们证明了超参数的设置会泄露隐私。
异常值会明显扭曲超参数的设置,这足以揭示异常值是否存在。
(2)我们提供工具来确保超参数的选择是满足差分隐私的,且隐私参数和满足重尾分布的重复次数之间的权衡
2.Background and Related Work
二、Motivation
文中利用SVM的超参数设置来举例,证明超参数设置的隐私性可以通过异常值显示出来。
SVM的损失函数如下所示:

并从正、负两类的各向同性2D高斯数据中提取100个输入,形成训练集d。负类以µ−1 =(−0.75,−0.75)为中心,正类以µ1 =(0.75,0.75)为中心。通过原始数据集D和D’(加入了2 outliers x 0 x_{0} x0 = (−2, 0))
α \alpha α为超参数

从上图可以看出,with outliers在 α \alpha α=40左右,就足以达到精度平台,而without outliers在增加 α \alpha α时,精度还有上升的趋势。
这样就可以利用这种差异,来执行成员推断攻击:在这里,可以从超参数 α \alpha α的值推断离群点 x 0 x_{0} x0是否是训练集的一部分。
三、Our Positive Results
1.Problem Formulation
文中假设有 M M M个算法 M 1 , M 2 , . . . , M n : X n → Y M_{1},M_{2},...,M_{n}:\mathcal{X}^{n} \rightarrow \mathcal{Y} M1,M2,...,Mn:Xn→Y,这意味着有 m m m个超参数。
接着做了两个假设:
1) Y \mathcal{Y} Y是有序的,这确保了存在最优。并且我们假设每个算法能输出一个质量分数以衡量该算法的效果,在这个过程中每个算法都会消耗一定的隐私预算。
2)输出既包含训练模型以及对应的超参数值
2.Strawman approach: repeat the base algorithm a fixed number of times
为了得到最优的结果,我们需要运行每个算法一次并且返回其评分结果。显然,隐私损耗的增长是线性的。并且,其结果不满足 ( m ε − τ , 0 ) − D P f o r τ > 0 (m \varepsilon-\tau, 0)-\mathrm{DP} for \tau>0 (mε−τ,0)−DPforτ>0, τ \tau τ指一个限制score范围的threshold。这个负面结果也延伸到 R e ˊ n y i D P Rényi DP ReˊnyiDP。为了避免这个问题,我们将随机运行基本算法几次。增加的不确定性大大增强了隐私。然而,我们必须仔细选择这个随机分布并分析它。
3.Our algorithm for hyperparameter tuning
为了获得良好的隐私边界,我们必须随机运行基本算法若干次。在实践中我们经常使用随机搜索而不是网格搜索。
具体来说,我们从某个分布中选取运行算法的总次数K,然后对于每一个k=1,…,k,我们随机均匀的选取一个index j k ∈ [ m ] j_{k} \in[m] jk∈[m],并运行 M j k M_{j_{k}} Mjk,最后,我们返回K个结果中最好的。
从本质上说,我们的目标是通过多次重复来“提高”Q的成功概率。必须选择运行次数K的分布,以确保良好的隐私保证,并确保系统可能选择良好的超参数设置。此外,系统的整体运行时间取决于K,我们希望运行时间是有效的和可预测的。我们的结果考虑了重复次数K的几种分布,以及这三种考虑之间的权衡。
个人理解:以上文SVM的超参数设置来举例,随机选取算法运行的总次数100,对于每一次的运行k,选取一个index j k ∈ [ m ] j_{k} \in[m] jk∈[m],并运行 M j k M_{j_{k}} Mjk,如 M 1 M_{1} M1,即对应超参数 α \alpha α具体值的选取
四、Main Results
重复次数k有许多可能的分布。在本节中,我们首先考虑两种——截断的负二项分布和泊松分布——并说明我们对这些分布的主要隐私结果。
负二项分布:
满足以下条件的称为负二项分布:
- 实验包含一系列独立的实验。
- 每个实验都有成功、失败两种结果。
- 成功的概率是恒定的。
- 实验持续到r次失败,r可以为任意正数。
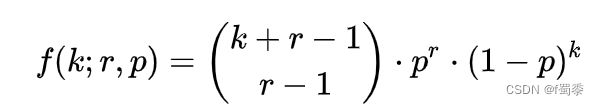
它表示,已知一个事件在伯努利试验中每次的出现概率是p,在一连串伯努利试验中,一件事件刚好在第r + k次试验出现第r次的概率
截尾分布: Experimental Evaluation 实验结果表明,在这种相对简单的超参数搜索中,泊松分布能够获得最佳的隐私-效用折衷。这与我们刚才给出的理论分析一致,即泊松分布在效用的中间范围内表现良好,因为这是一个简单的超参数搜索
截断分布是指,限制变量x取值范围(scope)的一种分布。
例如,限制x取值在0到50之间,即{0
为了证实这些发现,我们将我们的算法应用于一个真正的超参数搜索任务。具体来说,我们微调了在MNIST上训练的卷积神经网络的学习率。我们在JAX中实现了一种全卷积架构的DP-SGD,使用3x3内核生成的32、32、64、64、64个特征映射栈。我们在对数尺度上改变学习率在0.025和1之间,但固定所有其他超参数:60 epoch,小批量大小256,2裁剪范数1,噪声乘法器1.1。在图5中,我们绘制了在超参数搜索之前考虑的不同分布时获得的最大精度,作为搜索所消耗的总隐私预算的函数。实验重复500次,报告平均结果。五、Conclusion
