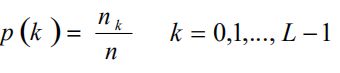增强旋转不变ＬＢＰ算法及其在图像检索中的应用

论文杂记
上一篇	主目录	下一篇

---

【 前言】

本论文是传统方法进行图像检索的论文之一，是基于内容的图像检索（Content-Based Image Retrieval，ＣＢＩＲ）。从关键词中可以看到本文使用到的主要算法。
关键词：经典LBP算法、LBP直方图、LBP旋转不变编码、ＥＬＢＰｒｉ描述符，Ｈａｒｒｉｓ算法，ＬＢＰ伪灰度图，欧氏距离
论文《增强旋转不变ＬＢＰ算法及其在图像检索中的应用》下载地址
或者联系博主获取，邮箱：[email protected]

---

1 预备知识

1.1 关于LBP

1.1.1 简介

局部二值模 式（Local Binary Pattern，ＬＢＰ）是一 种 描 述纹理特征的经典方法，该方法通过计算目标像素与其邻域内的像素之间的灰度差异来描述图像的局部纹理特征。
原始的LBP算子定义在3*3的窗口内，以窗口中心像素为阈值，将相邻的8个像素的灰度值与其进行比较，若周围像素值大于中心像素值，则该像素点的位置被标记为1，否则为0。3X3 邻域内的8个点可以产生8Bit的无符号数，转化为十进制数即得到该窗口的LBP值，并用这个值来反映该区域的纹理信息。

纹理特征在图像信息提取中的地位：
纹理特征是图像或图像局部区域所描述的景物的表面性质。与其他特征相比，纹 理 特 征 包 含 更 多 的图像信息。

1.1.2 LBP直方图

直方图有两种：
统计直方图

其中，

• n是总的个数
• nk是某一个取值的个数
  
  累积直方图
  
  
  LBP直方图就是用LBP的值构建城的直方图

1.1.3 圆形LBP算法

为了 使 经 典 ＬＢＰ特征适于描述不同尺度和不同频率的纹理信息，Ｏｊａｌａ等［１２］将３×３邻域扩展到任意邻域，并用 圆形窗口代替正 方 形 窗 口。改 进 后 的 ＬＢＰ描述 符 在 半 径 为 Ｒ的圆形邻域内拥有多个采样像素点。

左一LBP的右上标1代表半径是2，右下标8表示采样点的个数是8个
左一LBP的右上标2代表半径是2，右下标16表示采样点的个数是16个（网格交点处有采样点。。）
其他同理

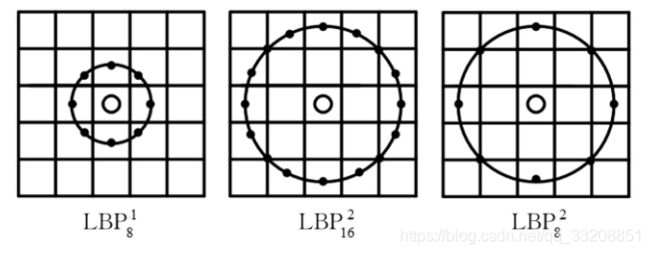
采样点位置（ｘｐ，ｙｐ）的计算：
对于给定的中心点（ｘｃ，ｙｃ），其邻域像素位置为（ｘｐ，ｙｐ），ｐ∈Ｐ，（ｘｐ，ｙｐ）用如下公式［１２］计算：

其中，Ｒ 是窗口半径，ｐ是采集的中心像素点周围的第ｐ 个像素，Ｐ 是采集的中心像素点周围的像素点个数。

【采样的点P（ｘｐ，ｙｐ）是落在圆圈上的？】
以(X_c,Y_c)为坐标原点，X_p²+Y_p²=R²

求每个采样点的过程：


由于式子计算出的坐标不一定在图像上，因此采用 双线性插值 (建议学习，见1.2）来计算采样点。也就是说，当采样点的P（ｘｐ，ｙｐ）坐标刚好与原图中的某点X（ｘ，ｙ）重合时，P点的灰度值或RGB的值就是原图中点X的值；如果采样点的x，y坐标没有与原图中的x，y重合时，就需要用到双线性插值法求P点的灰度值或RGB值。注：图像的像素点是离散型变量，当由上式计算出的P（ｘｐ，ｙｐ）有一个不是整形数字，那么P点就没与原图中某像素重合，此时使用双线性插值法求P点的灰度值或RGB值

1.1.4 旋转不变LBP

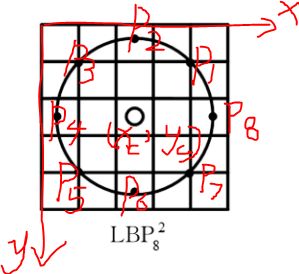
为满足旋转不变性，不断旋转圆形邻域的起始像素点，可以得到一系列 ＬＢＰ 值，取其中的最小值作为该邻域的 ＬＢＰ值。

白色为1，黑色为0
共有8位二进制数
LBP值的集合={240，120，60，30，15，135，195}
该邻域的LBP值为15
起始点：

240中顺时针方向第一个白色的点，二进制编码为11110000，即128+64+32+16+0+0+0+0=240
…
195中顺时针方向第三个白色的点，二进制编码为11000011，即128+64+0+0+0+0+2+1=195

【思考】

1. 这些点是从哪得来的，0和1如何得到？？？
   从1.1.3可知，这些点实际就是在某像素点作为中心点，通过公式采样得到的点，这些点的坐标可能是小数，也就是说，这些点的可能没有与在原图像的坐标系下与原图像的某像素点重合。但是，经过双线性插值已经求得了即使没有在源图像上有对应点的新图上的某像素点的灰度值的大小。
   通过比较这些采样到的点的灰度值与采样的中心原点的值的大小，灰度值比采样中心点大的采样点的值设为1，反之，小的设为0.
2. 为什么通过这种方式可以表示旋转不变的特性？？？
   当图像发生旋转时，圆形邻域内的灰度值gi是在以gc为中心R为半径的圆周上运动的。
   我们可以发现，只要我们取上述枚举出来的值的最小值，就可以消除旋转带来的影响。
   在该邻域内，取采样点LBP中最小值作为该邻域的LBP值。在这个邻域内的某种像素分布，例如纹理特征，是某种0、1分布的，当图相中纹理旋转时，因为纹理是一样的，所以对应的0、1序列只是整体上旋转了某个度数。而由于旋转LBP算法是将0、1序列依次旋转后化为二进制再转为十进制取最小值，所以纹理旋转后经过旋转LBP算法仍然能够得到相同的LBP值。所以具有旋转不变性。
   注：使用LBP最大值也可以表示旋转不变特性
3. 参数Ｐ＝８，Ｒ＝２时，Ｑ＝３６?
   百思不得其解，启发得源于：https://blog.csdn.net/qq_20823641/article/details/51456448 （中的四、旋转不变性LBP）
   当参数Ｐ＝８，Ｒ＝２时：
   
   先看一个例子：
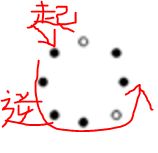
   我们得到一个二进制的LBP值10000011，然后不断对这个二进制进行向右循环移位（加上它本身，总共有8种取值可能），之后取最小结果就是该窗口的LBP值。结果分析看下图：
   
   当参数Ｐ＝８，Ｒ＝２时，共36种取值结果，取值结果如下图：
   
   （图中黑色是0，白色是1；这个图跟前面的起始点一致，但是从高位到低位是逆时针
   例如
   
   第二行第二列的二进制编码为：00001001
   第三行第三列的二进制编码为：00011101。（注意00011101跟00010111是不一样的））
   这是因为在这8个点的0、1序列的排列组合里面：
   以下向右循环移位
   1.全部是0只有一种情况00000000，LBP_min=0
   2.有1个1的情况：
   10000000、 01000000、 00100000、 00010000
   00001000、 00000100、 00000010、 00000001
   LBP_min=1
   3.有2个相邻1的情况：
   10000001、 11000000、 01100000、 00110000
   00011000、 00001100、 00000110、 00000011
   LBP_min=1+2=3
   4.有3个相邻1的情况：
   10000011、 11000001、 11100000、 01110000
   00111000、 00011100、 00001100、 00000111
   LBP_min=1+2+4=7
   …
   …
   …
   9.有8个相邻1的情况：
   11111111
   LBP_min=1+2+4+8+16+32+64+128=255
   10.有2个不相邻1且这两个1间隔为1的情况：
   10000010、 01000001、 10100000、 01010000
   00101000、 00010100、 00001010、 00000101
   LBP_min=1+ 4=5
   11.有2个不相邻1且这两个1间隔为2的情况：
   10000100、 01000010、 00100001、10010000
   01001000、 00100100、 00010010、 00001001
   LBP_min=1+ 8=9
   12.有2个不相邻1且这两个1间隔为3的情况：
   00010001
   LBP_min=1+ 16=17
   【有2个不相邻1且这两个1间隔为4的情况跟有2个不相邻1且这两个1间隔为的情况是一样的】
   13.有3个不相邻1的情况：
   00001011： LBP_min=1+ 2+8=11
   00001101： LBP_min=1+ 2+8=11（跟上式是不同情况，因为排成圆后按照顺时针或者逆时针方向遍历这些点，有一个不能取得1101的子序列）
   00010011： LBP_min=1+ 2+16=19
   00010101： LBP_min=1+ 4+16=21
   …
   …
   …
   就这么数，一共有36种不同的LBP取值。。。

1.2 双线性插值法

参考博文： 双线性插值 (建议学习）

主要思想总结如下：
我们知道，图像的像素点是离散型变量，当要对图像进行放大或缩小时，使用到了如下公式：

srcX=dstX * (srcWidth / dstWidth)
srcY=dstY * (srcHeight / dstHeight)
#src原图，dst目标图

【举个例子】
原图5X5，缩小成3X3。以图坐上角为坐标原点（0，0），往右是x轴正向，往下是y轴正向。

1. 新图3X3中点（0，0）在原图中对应的点是：
   srcX=0 * （5/3）
   srcY=0 * （5/3）
   那么
   srcX=0，srcY=0，即（0，0）
   新图中P（0，0）与原图中Q（0，0）两点完全重合，那么直接复制灰度值
2. 新图3X3中点（2，1）在原图中对应的点是：
   srcX=2 * （5/3）
   srcY=1 * （5/3）
   那么
   srcX=10/3，srcY=5/3，即（10/3，5/3）
   新图中（10/3，5/3）N点x，y都不是整数，在原图中找不到一点与之对应
   用双线性插值求灰度值：
   （1）先确定这个新点N落在哪4个像素点之间：10/3=3.33~，x轴落在3和4之间；5/3=1.66 ~，y轴落在1和2之间。因此可以知道，这个新点N落在这4个点之间：
   Q11（3，1），Q12（3，2），Q21（4，1），Q22（4，2）
   （2）在X方向上进行两次线性插值计算，然后在Y方向上进行一次插值计算
   
   在X方向上进行第一次线性插值计算得到R1：
   
   在X方向上进行第二次线性插值计算得到R2：
   
   然后在Y方向上进行一次插值计算得到P：
   
   注：以上式子中，f（Q）代表Q点的灰度值。因此f(x,y1)是R1的灰度值，f(x,y2)是R2的灰度值，f(x,y)是P的灰度值

以上是缩小的例子，放大图像类似

1.3 Harris角点检测

相关知识在上文《基于KNN有向复杂网络的图像轮廓识别》1.4节 中已有涉及，不再赘述。

1.4 欧氏距离

略

2 基于 ELBPri的图像检索系统

2.1 ELBPri的算法步骤

增强 ＬＢＰ纹理描述符即ELBPri的算法步骤如下：
总体思想，重要

1.在灰度图像中提取 Harris角点
2.以角点 为 采 样 中 心，在 角 点 周 围ｎ 像 素 范 围 内采样（n=5）
3.计算采样范围内图像区域的旋转不变 ＬＢＰ 值（对每个像素点），采样范围外图像区域的像素点的 ＬＢＰ值置为０
4.统计图像的ELBPri直方图，并将其作为 ＥＬＢＰｒｉ描述符的特征矢量
5.比 较 图 片 间 ＬＢＰ 直方图的相似性并排序

流程图：

2.2 Harris采样模式

原始的 ＬＢＰ算法中并没有采样的过程，而是直接采取遍历图像的方式。遍历图像虽然可以得到完整的纹理特征，但需要遍历图像中的每个像素点，并计算每个像素点的 ＬＢＰ值，耗时巨大，并且这将使得整个 ＣＢＩＲ 图像特征数据库的数据急剧增多。为减少数据库的数据量，本 文 采 用 Ｈａｒｒｉｓ角点提取算法对原图片进行采样。图像像素点中距离角点小于或等于ｎ像素的所有像素点为有效区域，大于ｎ像素的为无效区域。如图５所示，以ｎ＝５为例，黑色圆点为角点，斜线覆盖的像素点构成有效区域，其他像素点为无效区域。将 无 效 区域在 ＬＢＰ伪灰度图像中 的 ＬＢＰ值置 为０，保 留 有 效 区 域，即完成了采样过程。采样过程定义如下：

其中，Ａｅ 表示有效 区 域，Ａｉ 表示 无 效 区 域，Ｄ 表示 像 素 点 与最近角点的距离。

对原图像进行采样，可以极大地降低下一步用旋转不变ＬＢＰ算法描述图像时的工作 量，并剔除无效区域对图像检索的影响，增强了图像检索的鲁棒性。

2.3 ELBPri算法描述符的构建

利用 旋 转 不 变 ＬＢＰ描述符的编码方法对采样后的图片进行编码，获得原图像的 ＥＬＢＰｒｉ伪灰度图像
ＥＬＢＰｒｉ伪灰度图像的形式化定义为：

其中，（ｘ，ｙ）∈Ａｅ，（ｘ，ｙ）是有效区域像素点坐标。Ｇx,y∈｛０，１，…，Ｑ｝是图像所有 微 模 式 的 ＬＢＰ值集 合，Ｑ 是图 像 最 大 的ＬＢＰ值（参数Ｐ＝８，Ｒ＝２时，Ｑ＝３６）。

【伪灰度图像和编码】
在用Harris采取特征样点后（此时得到的图像上好多个点Xi），与这些点距离小于D（=5）的为有效区域，其他无效区域的所有像素点的LBP值为0。对在有效区域内的所有点：使用1.1.3圆形LBP算法在有效区域所有像素点的邻域内得到多个采样像素点（不一定在图像上，则使用1.2双线性插值法），求这些点的灰度值，跟邻域中心点比较，大的为1，小的为0。使用1.1.4旋转不变LBP求得的最小LBP值作为以该像素点为中心邻域的LBP值（有效区域内每个像素点都有以该像素点为中心的邻域，对应有一个邻域LBP值）。在原图像上用求得的每个像素邻域的LBP值作为该像素新的灰度值，即获得原图像的 ＥＬＢＰｒｉ伪灰度图像 。这幅伪灰度图像的LBP值的某种集合方式作为这个图像的编码。
【参数Ｐ＝８，Ｒ＝２时，Ｑ＝３６?】
为啥？？？见1.1.4-3

2.4 相似度对比

• 基于 ＥＬＢＰｒｉ算法对图像进行纹理特征提取后，还 需 要将计算出的 ＬＢＰ值转化成特征向量，从而依据特征向量来对比图像的 相 似 度。
• 本文在图像转化成 ＬＢＰ 值后，通 过 ＬＢＰ直方图体现图像 的 纹 理。
• 利用邻域旋转不变 ＬＢＰ算子 可 得到 ＬＢＰ的取值范围为［０，３６］。将这个区间平均分成３６个小区间段［０，１，…，３６］，- - 通过 统 计 图 像 ＬＢＰ值落到每个区间的个数，最终形成３６维 ＬＢＰ直方图。
• 采用下式计算待匹配图像的 ＥＬＢＰｒｉ直方图间的欧氏距离 Ｄｋ［１４］，Ｄｋ 越小，则 查 询 图像与图像库中第ｋ个图像 越 相 似。按 照 Ｄｋ 从小到大排序输出查询结果，实现检索功能。
  

2.5 ELBPri描述符优点

１）保 留 ＬＢＰ描述符的部分微模式，并使 ＬＢＰ具有 了 旋转不变性。ＥＬＢＰｒｉ算法没有从压缩微模式数量的角度改进算法，而是在提取描述子之前加了采样过程，这样既保留了部分微模式和描述符的旋转不变性，又提高了算法的效率。
２）计 算 量 小，效 率 高。ＥＬＢＰｒｉ算法 借 助 于 Ｈａｒｒｉｓ角点提取算法标定出纹理信息丰富的区域，在提取描述子前添加了采样过程，降低了生成 ＬＢＰ伪灰度图时的计算量和需要存储的数据量，提高了算法的效率。
３）突出纹理信息丰富区域的纹理信息，去除部分噪声，鲁棒性高。纹理信息丰富区域的角点数量多，ＥＬＢＰｒｉ算法的采样过程突出了纹理信息丰富的区域。同时，纹理信息简单、噪声点等区域在采样过程中被滤去。