数学建模——遗传算法步骤及程序详解
数学建模——遗传算法步骤及程序详解
文章目录
- 数学建模——遗传算法步骤及程序详解
- 前言
- 一、遗传算法的基础
-
- 1、编码和解码
- 2、适应度函数
- 3、交叉
- 4、变异
- 5、选择
- 二、遗传算法原理步骤
-
- 1、初始化参数
- 2、编码和解码
- 3、选择子代
- 三、编程和代码
- 总结
前言
遗传算法是一种基于生物染色体遗传时发生交叉、变异的原理,是一种通过模拟自然进化过程,对解集进行优化更新的算法,属于优化算法的一种。
一、遗传算法的基础
遗传算法是基于生物染色体遗传时发生的原理,那么就要先了解一下生物学关于遗传的基本原理。假设种群为P(t),下一代种群为P(t+1)
遗传:P(t)中优良个体传到下一代群体P(t+1)
交叉:P(t)内个体随机搭配,对每一个体以某个概率交换部分染色体
变异:P(t)内个体以某一个概率改变一个或一些基因
进化:种群逐渐适应生存环境,品质不断得到改良。生物的进化是以种群的形式进行的。
适应度:物种对生存环境的适应程度
1、编码和解码
说起编码首先我们可以想到的就是计算机二进制编码方式,我们首要做的就是将解变化为二进制编码。经典遗传算法中使用“染色体”来代指个体,它由二进制串组成,如下图所示:

上图可以认为是一个染色体,其中1-0代表基因,( i i i)代表基因的位置。
我们首先明确,编码长度取决于自变量的范围(更准确点应该是决策变量的范围)和搜索精度,所以围绕它们来考虑如何编码。
基因的维度就代表可以存储的信息,(例如000001代表1),6维的基因转为10进制可以表示 2 6 2^6 26的数字,每增加一维,可以存储的数字都是成倍增加。但是这里就会产生一个问题,二进制表达的数值都是倍数上升的,有时候不会那么恰巧就会是 2 n 2^n 2n。
首先,我们可以确定自变量的范围(更准确点应该是决策变量的范围)例如(2,7),假设,我们需要的精度是0.01,那么一共就会有500个数值,而大于500且最接近500的数值就是 2 9 2^9 29,9位数的二进制可以表示512-1=511个数字,我们可以将二进制编码如下:
A 1 A 2 A 3 ⋯ A 9 A_1A_2A_3\cdots A_9 A1A2A3⋯A9
编码后一共可以有511个数值,明显多于我们的(2,7)的0.01精度的取值范围,编码的时候我们是把5放大到511,那么解码时缩小511倍就行了。
我们解码的时候就可以做如下处理:
δ = 5 511 ≈ 0.00978 \delta =\frac{5}{511}\approx0.00978 δ=5115≈0.00978
先将二进制编码转化为十进制:
A = ∑ i = 1 n A i 2 i − 1 A=\sum_{i=1}^n{A_i2^{i-1}} A=i=1∑nAi2i−1
再将解码出来的十进制数都乘以0.00978,就得到了最终结果.
x = L X + δ A = L X + δ ∑ i = 1 n A i 2 i − 1 x=L_X+\delta A=L_X+\delta\sum_{i=1}^n{A_i2^{i-1}} x=LX+δA=LX+δi=1∑nAi2i−1
这里 L X L_X LX代表区间的下限
这里大家可以回顾一下编码和解码的过程,普通二进制编码是遗传算法最常见的编码方式,大家以后学得更深一点会有格雷编码、浮点编码法、符号编码法等等一些进阶的编码方法,这里就不再展开,大家有兴趣可以自己去了解一下。
2、适应度函数
适应度是物种对生存环境的适应程度,那么在遗传算法的过程中,适应度其实就是解对应的函数,在规划模型中也称为目标函数。
①最小化问题
令适应度:
F ( f ( x ) ) = { f x − C m i n , f ( x ) > C m i n 0 , o t h e r F(f(x))= \left\{ \begin{array}{lr} f_{x}-C_{min}&,f(x)>C_{min}\\ 0&,other \\ \end{array} \right. F(f(x))={fx−Cmin0,f(x)>Cmin,other
其中 C m i n C_{min} Cmin当前最小估计值
②最大化问题
令适应度:
F ( f ( x ) ) = { C m a x − f x , f ( x ) < C m a x 0 , o t h e r F(f(x))= \left\{ \begin{array}{lr} C_{max}-f_{x}&,f(x)
其中 C m a x C_{max} Cmax当前最大估计值
这里介绍了最大化和最小化的两种问题,其实在适应度这里还有一个和约束条件相关的罚函数问题,为了解决函数的约束条件,在约束条件之外的解会增加函数适应度,距离约束条件越大,罚函数的惩罚力度越大。
②外点法罚函数问题
F ( x , λ ) = f ( x ) + λ P ( x ) F(x,λ)=f(x)+λP(x) F(x,λ)=f(x)+λP(x)
P ( x P(x P(x)的定义一般如下:
P ( x ) = ∑ i = 1 m ψ ( g i ( x ) ) + ∑ j = 1 l Φ ( h j ( x ) ) P\left( x \right) =\sum_{i=1}^m{\psi \left( g_i\left( x \right) \right) +\sum_{j=1}^l{\varPhi \left( h_j\left( x \right) \right)}} P(x)=i=1∑mψ(gi(x))+j=1∑lΦ(hj(x))
其中 ψ ( g i ( x ) ) \psi (g_i(x)) ψ(gi(x))是关于不等式约束的函数,当 x x x在不等式约束条件内时, ψ ( g i ( x ) ) \psi (g_i(x)) ψ(gi(x))为零,不满足约束条件时, ψ ( g i ( x ) ) \psi (g_i(x)) ψ(gi(x))大于零;同理 Φ ( h j ( x ) ) \varPhi \left( h_j\left( x \right) \right) Φ(hj(x))是关于等式约束的函数。即,当点 x x x在可行域内, F = f F =f F=f,在可行域外,F越来越大。
ψ 、 Φ \psi 、Φ ψ、Φ一般定义如下:
ψ = [ max ( 0 , − g i ( x ) ) ] a , Φ = ∣ h j ( x ) ∣ b \psi =\left[ \max \left( 0,-gi\left( x \right) \right) \right] ^a,\varPhi =|h_j\left( x \right) |^b ψ=[max(0,−gi(x))]a,Φ=∣hj(x)∣b
一般情况取a=b=2
上面的公式合并起来就是
F ( x , λ ) = f ( x ) + λ { ∑ i = 1 m max ( 0 , g i ( x ) ) 2 + ∣ h i ( x ) ∣ 2 } F\left( x,\lambda \right) =f\left( x \right) +\lambda \left\{ \sum_{i=1}^m{\max\text{\ }\left( 0,gi\left( x \right) \right) ^2+|h_i\left( x \right) |^2} \right\} F(x,λ)=f(x)+λ{i=1∑mmax (0,gi(x))2+∣hi(x)∣2}
λ \lambda λ为惩罚因子,是一个单调递增正值序列, λ ( k + 1 ) = e λ k \lambda^{(k+1)}=e\lambda^{k} λ(k+1)=eλk,经验表明当e取[5,10]、 λ ( 1 ) = 1 \lambda^{(1)}=1 λ(1)=1的结果是相对满意的。
3、交叉
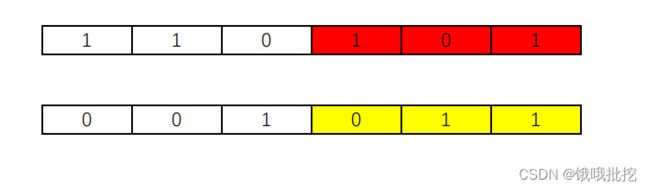
两个染色体的某一相同位置处DNA被切断,前后两串分别交叉组合形成两个新的染色体,也称为基因重组或杂交,我们用下面的例子来说明,如下图: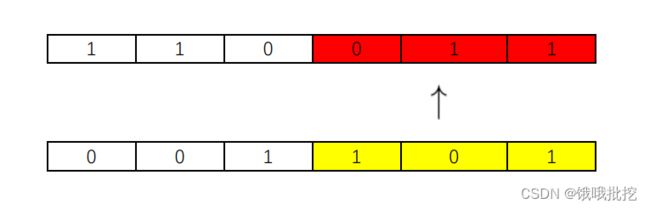
以上就是两个父代染色体,他们选择一段相同位置的片段进行交叉互换就可以得到两个全新的子代,如下图
以上就是一种交叉的方式,还有很多奇奇怪怪的交叉方法,这里不再一一举例,但本质都是截取一个染色体的片段,和其他染色体片段进行交叉交换,有兴趣的同学可以看一下其他交叉的方法,链接附在下方。
https://blog.csdn.net/u012750702/article/details/54563515
4、变异
变异就简单得多了,只要把交叉过后的编码,随机选择一个位置,由0变为1或者由1变为0即可。也有其他的变异方法,变异方式是随机选择父代染色体上的几个基因位置,然后重新排列,其他位置保持不变。
变异和交叉的区别就在于交叉是两个个体的,而变异是本身。变异的方法同样是千奇百怪,有兴趣的可以了解,链接附在下方。
https://blog.csdn.net/u011001084/article/details/49450051
5、选择
在对个体的适应度进行评价的基础上,通过选择操作把优化的个体直接遗传到下一代,或通过配对交叉产生新的个体再遗传到下一代。设群体规模为m,个体i的适应度为Fi,则个体i被选中的概率Pis为
P i s = F i ∑ i = 1 m F i P_{is}=\dfrac{F_i}{\sum\limits_{i=1}^m{F_i}} Pis=i=1∑mFiFi
二、遗传算法原理步骤
1、初始化参数
生成初始解集后,首先根据选择率,比如选出一定比例的个体进行交叉、变异过程
2、编码和解码
十进制数转为二进制数后,由多个0个1组成,看起来比较像染色体,交叉过程是首位一段区域的0和1进行位置交叉互换,变异则是直接进行概率性的0-1变更,得到新的自变量后再代入函数算出解。
3、选择子代
这90%个体得到新的子代解集后,按优到劣进行排列,原父代解集则按列到优排列,并将前90%的解集直接替换为新的自带解集(简单理解就是不断把最劣的90%解集重新经过交叉、变异过程得到新的解集,其中可能会产生更优的解集)
因此,特别需要注意的是不能把选择率(也叫代沟)设为100%,虽然每次循环都有最优值记录,这样也能更快得到最优值,但是违背了算法原理,算法会近似变成蒙特卡洛模拟。
三、编程和代码
matlab代码如下:
%遗传算法只能借鉴,因为题目要解决的题不一样,只能借鉴框架,本文代码借鉴了网上的代码
%有疑问可以私聊作者,QQ:2892053776
%先画出大概图像,方便我们后续比较
clc,clear
%遗传算法求解
%matlab是内嵌由遗传工具箱的(不懂的可以百度matlab遗传工具箱)‘
opt_minmax=1; %目标优化类型:1最大化、-1最小化
num_ppu=50; %种群规模:个体个数
num_gen=100; %最大遗传代数
len_ch=9; %基因长度(二进制位数)
gap=0.9; %代沟
ub=-1.5; %变量取值下限
up=3.5; %变量取值上限
k_gen=0; %初始化遗传次数
cd_gray=0; %是否选择格雷编码方式:1是0否
sc_log=0; %是否选择对数标度:1是0否
trace=zeros(num_gen,2); %遗传迭代性能跟踪器,生成60行2列0矩阵
chrom=crtbp(num_ppu,len_ch); %初始化生成种群,生成一个50*20的矩阵,矩阵元素是0-1随机数
%这里没办法运行的可以百度一下安装gatbx遗传包
fieldd=[len_ch;ub;up;1-cd_gray;sc_log;0;0]; %区域描述器
x=bs2rv(chrom,fieldd); %翻译初始化种群为10进制
fun_v=fun_sigv(x); %计算目标函数值
tx=ub:.01:up;
plot(tx,fun_sigv(tx))
xlabel('x')
ylabel('y')
title('一元函数优化结果')
hold on
while k_genfunction y=fun_sigv(x)
y=x.*cos(5*pi*x)+2.*x.^2+3.5;
总结
遗传算法本身就是寻优算法,也可以用到解决旅行商问题。而且遗传算法是看脸的,有时候哪怕迭代次数和种群密度都上去了,也可能找不到理想解,有时候可能一次就跑出结果。
在实际过程操作中,问题千变万化,目标函数也千变万化,也就决定了目标函数、交叉、变异这几个过程是比较复杂多变的,需要根据需要自己灵活变化。
优点
1:优化结果与初始条件无关。
2:搜索从群体出发,具有潜在的并行性,可以进行多个个体的同时比较。
3:搜索使用评价函数启发,过程简单。
4:具有可扩展性,容易与其他算法结合。(遗传模拟退火算法)
缺点
1:收敛速度慢,且无数学证明n趋近无穷时一定收敛。
2:局部搜索能力差。
3:控制变量较多。
4:无确定的终止准则。