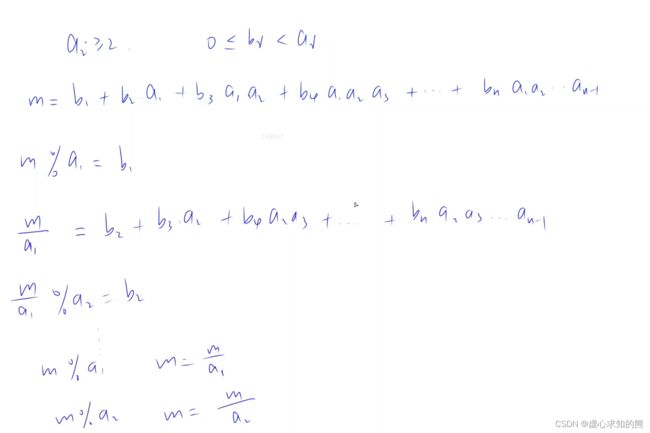AcWing - 寒假每日一题2023(DAY 11——DAY 15)
文章目录
- 一、AcWing 4656. 技能升级(困难)
-
- 1. 实现思路
- 2. 实现代码
- 二、AcWing 4454. 未初始化警告(简单)
-
- 1. 实现思路
- 2. 实现代码
- 三、AcWing 4509. 归一化处理(简单)
-
- 1. 实现思路
- 2. 实现代码
- 四、AcWing 4699. 如此编码(简单)
-
- 1. 实现思路
- 2. 实现代码
- 五、AcWing 4700. 何以包邮?(简单)
-
- 1. 实现思路
- 2. 实现代码
一、AcWing 4656. 技能升级(困难)
题目描述
小蓝最近正在玩一款 RPG 游戏。
他的角色一共有 N 个可以加攻击力的技能。
其中第 i 个技能首次升级可以提升 Ai 点攻击力,以后每次升级增加的点数都会减少 Bi。
⌈Ai / Bi⌉(上取整)次之后,再升级该技能将不会改变攻击力。
现在小蓝可以总计升级 M 次技能,他可以任意选择升级的技能和次数。
请你计算小蓝最多可以提高多少点攻击力?
输入格式
输入第一行包含两个整数 N 和 M。
以下 N 行每行包含两个整数 Ai 和 Bi。
输出格式
输出一行包含一个整数表示答案。
数据范围
对于 40% 的评测用例,1 ≤ N,M ≤ 1000;
对于 60% 的评测用例,1 ≤ N ≤ 104,1 ≤ M ≤ 107;
对于所有评测用例,1 ≤ N ≤ 105,1 ≤ M ≤ 2×109,1 ≤ Ai,Bi ≤ 106。
输入样例
3 6
10 5
9 2
8 1
输出样例
47
具体实现
1. 实现思路
- 这类问题比较困难,因此,首先我们先写出一个正确的过程,随后在对过程进行优化,避免超时的问题。
- 可以把每一个技能看作是一个等差数列,将所有技能从大到小排序,选择前 m 个数肯定是最大的。
- 第一次选的的最大值一定是每个等差数列第一个数字当中的最大值,继续选的时候就是在该等差数列的下一个值与其他等差数列的第一个值进行比较选最大值。
- 对于上述过程,我们可以将整体进行从大到小的排列,然后选择出其中第 m 个数,然后升级所得攻击力的最大值就是前 m 个数进行求和,选择第 m 个数的过程可以使用二分查找进行解决。
- 我们假设第 m 个数的值是 x,那么大于等于 x 的数的个数应该大于等于 m 个,大于等于 x+1 的数的个数应该小于 m 个。
- 在找出第 m 个数后,需要对前面的数进行求和即可。
2. 实现代码
#include 二、AcWing 4454. 未初始化警告(简单)
题目描述
一个未经初始化的变量,里面存储的值可能是任意的。
因此直接使用未初始化的变量,比如将其赋值给另一个变量,并不符合一般的编程逻辑。
代码中出现这种情况,往往是因为遗漏了初始化语句、或是打错了变量名。
对代码中使用了未初始化变量的语句进行检查,可以方便地排查出代码中的一些隐秘 Bug。
考虑一段包含 k 条赋值语句的简单代码。
该段代码最多使用到 n 个变量,分别记作 a1,a2,⋯,an;该段代码使用的常量均记作 a0。
第 i 条(1 ≤ i ≤ k)赋值语句为 axi = ayi,满足 1 ≤ xi ≤ n、0 ≤ yi ≤ n,表示将 ayi 的值赋给变量 axi。
其中 axi 被称为该赋值语句的左值,一定是个变量;ayi 被称为右值,可以是一个常量或变量。
对于任意一条赋值语句 axi = ayi,如果右值 ayi 是一个变量,则其应该在此之前被初始化过。
具体来说,如果变量 ayi 在前 i−1 条赋值语句中做为左值出现过,即存在 j < i 满足 xj = yi(这里无需考虑第 j 条赋值语句本身是否也有右值未初始化的问题),我们就认为在第 i 条赋值语句中 ayi 已被初始化;否则,我们认为该条语句存在右值未初始化的问题。
按照上述规则,试统计给定的代码中,有多少条赋值语句右值未被初始化。
输入格式
输入的第一行包含空格分隔的两个正整数 n、k,分别表示变量的数量和赋值语句的条数。
接下来输入 k 行,其中第 i 行(1 ≤ i ≤ k)包含空格分隔的两个正整数 xi、yi,表示第 i 条赋值语句。
纠错:其实 yi 可以等于 0,所以 yi 不一定是正整数(可参考样例),此为官网题面描述存在问题,特此指出。
输出格式
输出一个整数,表示有右值未被初始化问题的赋值语句条数。
数据范围
50% 的测试数据满足 0 < n,k ≤ 1000;
全部的测试数据满足 0 < n,k ≤ 105,1 ≤ xi ≤ n,0 ≤ yi ≤ n。
输入样例
10 7
1 2
3 3
3 0
3 3
6 2
2 1
8 2
输出样例
3
样例解释
其中第一、二、五条赋值语句右值未被初始化。
具体实现
1. 实现思路
- 这道题的内容很长,因此,我们需要对其进行精简。
- 等号左边被称为左值,等号右边被称为右值,以 x=y 为例,x 就是左值,y 就是右值。
- 如果 y 不是常量且没有被赋值,则该语句便没有意义,最后判断有多少个语句没有意义即可。
- 在其中,例如存在 x=y,z=x 这两条语句,则第一句没有意义,第二句有意义。因为虽然第一句没有意义,但是我们仍认为 x 被赋值过了。
- 对样例做解释,第一句当中的右值 2 不是常量(也就是 0)且没有被赋值,则第一句没有意义,但此时 1 已被赋值过了。
- 第二句与第一句同理,但 3 已被赋值过了。
- 第五句也是同理,但在第六句当中,2 被赋值则后续均无问题。
2. 实现代码
#include 三、AcWing 4509. 归一化处理(简单)
题目描述
输入格式
第一行包含一个整数 n,表示待处理的整数个数。
第二行包含空格分隔的 n 个整数,依次表示 a1,a2,⋯,an。
输出格式
输出共 n 行,每行一个浮点数,依次表示按上述方法归一化处理后的数据 f ( a 1 ) f(a_{1}) f(a1), f ( a 2 ) f(a_{2}) f(a2),⋯, f ( a n ) f(a_{n}) f(an)。
如果你输出的每个浮点数与参考结果相比,均满足绝对误差不大于 10−4,则该测试点满分,否则不得分。
数据范围
全部的测试数据保证 n,|ai| ≤ 1000,其中 |ai| 表示 ai 的绝对值。
且输入的 n 个整数 a1,a2,⋯,an 满足:方差 D ( a ) D(a) D(a) ≥ 1。
输入样例
7
-4 293 0 -22 12 654 1000
输出样例
-0.7485510379073613
0.04504284674812264
-0.7378629047806881
-0.7966476369773906
-0.7057985054006686
1.0096468614303775
1.9341703768876082
样例解释
平均值: a ˉ \begin{aligned}\bar{a}\end{aligned} aˉ ≈ 276.14285714285717
方差: D ( a ) \begin{aligned}D(a)\end{aligned} D(a) ≈ 140060.69387755104
标准差: D ( a ) \begin{aligned}\sqrt{D(a)}\end{aligned} D(a) ≈ 374.24683549437134
具体实现
1. 实现思路
- 本题直接带入公式求解即可,较为简单。
- 首先读入每一个整数,在此过程当中顺带求和。
- 完成求和后直接求平均值即可,这里需要注意的是要使用 double 类型,因为要误差不小于 10−4。
- 在求完平均值后求解方差,使用 pow(x,y) 函数,表示用来求 x 的 y 次幂。
- 使用sqrt() 函数,用以求解标准差。
- 最后代入公式即可求得 f ( a i ) f(a_{i}) f(ai)。
2. 实现代码
#include 四、AcWing 4699. 如此编码(简单)
题目描述
输入格式
输入共两行。
第一行包含用空格分隔的两个整数 n 和 m,分别表示题目数量和顿顿老师的神秘数字。
第二行包含用空格分隔的 n 个整数 a1,a2,⋯,an,依次表示每道选择题的选项数目。
输出格式
输出一行包含一个整数表示答案。输出仅一行,包含用空格分隔的 n 个整数 b1,b2,⋯,bn,依次表示每道选择题的正确选项。
数据范围
50% 的测试数据满足:ai 全部等于 2,即每道题均只有两个选项,此时 ci = 2i;
全部的测试数据满足:1 ≤ n ≤ 20,ai ≥ 2 且 cn ≤ 109(根据题目描述中的定义 cn 表示全部 ai 的乘积)。
输入样例 1
15 32767
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
输出样例 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
输入样例 2
4 0
2 3 2 5
输出样例 2
0 0 0 0
输入样例 3
7 23333
3 5 20 10 4 3 10
输出样例 3
2 2 15 7 3 1 0
样例 3 解释
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| ai | 3 | 5 | 20 | 10 | 4 | 3 | 10 |
| bi | 2 | 2 | 15 | 7 | 3 | 1 | 0 |
| ci-1 | 1 | 3 | 15 | 300 | 3000 | 12000 | 36000 |
提示
具体实现
1. 实现思路
- 此题与进位制较为类似,可假设 a 为 10 进行体会。
- 因此,当我们求解 b 的时候,就可近似理解为求解进制当中的每一位(求模再整除,再求模再整除,以此类推)。
- 此类题往往题目复杂但实际上较为简单,需要理性分析,具体的计算过程如下:
2. 实现代码
#include 五、AcWing 4700. 何以包邮?(简单)
题目描述
新学期伊始,适逢顿顿书城有购书满 x 元包邮的活动,小 P 同学欣然前往准备买些参考书。
一番浏览后,小 P 初步筛选出 n 本书加入购物车中,其中第 i 本(1 ≤ i ≤ n)的价格为 ai 元。
考虑到预算有限,在最终付款前小 P 决定再从购物车中删去几本书(也可以不删),使得剩余图书的价格总和 m 在满足包邮条件(m ≥ x)的前提下最小。
试帮助小 P 计算,最终选购哪些书可以在凑够 x 元包邮的前提下花费最小?
输入格式
输入的第一行包含空格分隔的两个正整数 n 和 x,分别表示购物车中图书数量和包邮条件。
接下来输入 n 行,其中第 i 行(1 ≤ i ≤ n)仅包含一个正整数 ai,表示购物车中第 i 本书的价格。
输入数据保证 n 本书的价格总和不小于 x。
输出格式
仅输出一个正整数,表示在满足包邮条件下的最小花费。
数据范围
70% 的测试数据满足:n ≤ 15;
全部的测试数据满足:n ≤ 30,每本书的价格 ai ≤ 104 且 x ≤ a1+a2+⋯+an。
输入样例 1
4 100
20
90
60
60
输出样例 1
110
样例 1 解释
购买前两本书 (20+90) 即可包邮且花费最小。
输入样例 2
3 30
15
40
30
输出样例 2
30
样例 2 解释
仅购买第三本书恰好可以满足包邮条件。
输入样例 3
2 90
50
50
输出样例 3
100
样例 3 解释
必须全部购买才能包邮。
具体实现
1. 实现思路
- 一共有 n 本书,这 n 本书可以选择也可以不选择,就一共有 2n 种情况。
- 对于 70% 的数据,可以直接使用暴力的方法进行操作,举个例子就是,如果是 4 本书,就使用 4 位的二进制数字,1 表示选择,0 表示不选,依次枚举即可(可以用 <<(乘 2) 和 >>(除 2) 表示)。
- 正解就是一种背包问题,需要将原问题转化位一个新的问题。
- 可以先计算一下买所有书的总价格,将其定为 sum,然后依次去掉书,使得总价格在大于等于 x(买书的包邮条件)的情况下买的书越小越好。
- 那么,就可以将其转换为我们选择几本书,使得这几本书的总价格在不超过 sum-x 的情况下,总价格越大越好(转换位经典的 0-1 背包问题)。
- 背包容量就是 sum-x,每个物品的体积就是 w[i],每个物品的价值也是 w[i]。
2. 实现代码
#include