jeremy的路径规划学习-1.三维地图定义，散点拟合插值与粒子群算法（matlab实现）

jeremy的路径规划学习-1.三维地图定义，散点拟合插值与粒子群算法（matlab实现）

本文基于小黎的ally学习资料实现，感谢该博主的无私奉献

三维地图与二维地图的差别

1.二维无高度信息，多用于地面机器人，自动驾驶
2.二维地图路径规划有：全覆盖路径规划（室内），利用地图软件的全局路径规划，在道路的局部路径规划
3.三维地图涵盖高度深度信息，多用于无人机、水下机器人等。

三维地图的山峰数学模型

三维空间曲线性质（用来计算适应度等）

◆ 二维平面曲线可以用“曲率”描述曲线的弯曲程度，一般来说平面路径规划要求曲率连续无突变；
◆ 在三维空间中，曲线用两个指标进行描述，即曲率（curvature）和挠率（torsion），同样也要求
曲率和挠率都连续无突变。
◆ Matlab的polyfit函数可以对二维散点进行多项式曲线的拟合，但是与散点的坐标大小顺序有关，且
不方便拓展到三维空间。
◆ 参照B样条曲线/贝塞尔曲线的生成原理，将散点的x/y/z坐标分别看成参数t的函数值，并令参数t的
范围为[0,1]，分别代表第一个散点和最后一个散点，再利用spline函数可以实现三维散点的光滑连
接

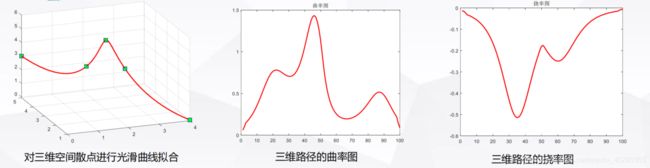
下面是三维地图生成代码（带注释）

%% 初始化地形信息
mapRange = [100,100,100];           % 地图长、宽、高范围
N = 10;                             % 山峰个数
%struct 结构体(字段下数据类型不限)
peaksInfo = struct;                 % 初始化山峰特征信息结构体
peaksInfo.center = [];              % 山峰中心
peaksInfo.range = [];               % 山峰区域
peaksInfo.height = [];              % 山峰高度
%repmat用来矩阵堆叠，将peaksInfo矩阵块当作一个元素按照N*1的矩阵排布
peaksInfo = repmat(peaksInfo,N,1); 
%% 随机生成N个山峰的特征参数
for i = 1:N
    peaksInfo(i).center = [mapRange(1) * (rand*0.8+0.2), mapRange(2) * (rand*0.8+0.2)];
    peaksInfo(i).height = mapRange(3) * (rand*0.7+0.3);
    %生成山峰范围，范围越大，山峰的坡度越缓。
    peaksInfo(i).range = mapRange*0.1*(rand*0.7+0.3);
end

%% 计算山峰曲面值
peaksData = [];
for x = 1:mapRange(1)
    for y = 1:mapRange(2)
        sum = 0;
        for k = 1:N
            h_i = peaksInfo(k).height;
            x_i = peaksInfo(k).center(1);
            y_i = peaksInfo(k).center(2);
            x_si = peaksInfo(k).range(1);
            y_si = peaksInfo(k).range(2);
            %三维地图数学模型
            sum = sum + h_i * exp(-((x-x_i)/x_si)^2 - ((y-y_i)/y_si)^2);
        end
        %将x,y分别带入计算整个地图的高度信息
        peaksData(x,y) = sum;
    end
end

%% 构造曲面网格，用于后期MAP图插值判断三维路径是否与山峰交涉

% x列向量，不断纵向扩充，每隔一百个就增大1
x = [];
for i = 1:mapRange(1)
    x = [x; ones(mapRange(2),1) * i];
end

% y列向量
%加’意思是y纵向列向量排布，如果不加，就是行向量排布。
y = (1:mapRange(2))';
%peaksData(:)是将整个矩阵展开成一列且纵向展开，按列展开后连接
%y是1-100，1-100循环100次
y = repmat(y,length(peaksData(:))/length(y),1);

% peaksData列向量，reshape是矩阵竖着展开后重新竖着排布
peaksData = reshape(peaksData,length(peaksData(:)),1);

% 构造X/Y/Z网格数据
%griddate：griddata(x,y,z,XI,YI)用二元函数z=f(x,y)的曲面拟合有不规则的数据向量x,y,z。
%griddata 将返回曲面z 在点（XI,YI）处的插值
%linspace 线性等间距插值，后面数字控制网格精度
%x,y已经限制在100以内了
[X,Y,Z] = griddata(x,y,peaksData,...
    linspace(min(x),max(x),100)',...
    linspace(min(y),max(y),100));

%% 画山峰曲面
surf(X,Y,Z)      % 画曲面图
shading flat     % 各小曲面之间不要网格

那已知三维点，如何进行拟合散点呢？
脚本如下：

%% 根据散点获得拟合曲线三维路径
x_seq = [0,1,2,3,4];
y_seq = [5,2,3,4,1];
z_seq = [3,4,5,2,0];

% 利用spline函数进行拟合插值
k = length(x_seq);
t_seq = linspace(0,1,k);
%分成100份是进一步离散化
T_seq = linspace(0,1,100);
%spline:三次方样条数据插值
X_seq = spline(t_seq,x_seq,T_seq);
Y_seq = spline(t_seq,y_seq,T_seq);
Z_seq = spline(t_seq,z_seq,T_seq);

% 画拟合曲线图
figure
%最开始的点顺序不一样应该拟合曲线也不同
%scatter3：三维散点图
scatter3(x_seq, y_seq, z_seq, 100, 'bs','MarkerFaceColor','g')
hold on
%plot3:三维曲线
plot3(X_seq, Y_seq, Z_seq, 'r','LineWidth',2)
grid on
title('散点拟合曲线')

%% 计算曲线的曲率、挠率
% 计算三阶导数
f = [X_seq; Y_seq; Z_seq];          % 表示函数
delta = 1 / length(X_seq);
%grandient:求梯度，若x为多维矩阵，例如[Fx,Fy]=gradient(x)
%左边界梯度： Fx(:,j) = Fx(:,j+1) - Fx(:,j) ；
%右边界梯度： Fx(:,j) = Fx(:,j) - Fx(:,j-1);
%中间区域梯度： Fx(:,j) = (Fx(:,j+1) - Fx(:,j-1)) / 2.
f1 = gradient(f)./delta;            % 一阶导
f2 = gradient(f1)./delta;           % 二阶导
f3 = gradient(f2)./delta;           % 三阶导
f1 = f1';
f2 = f2';
f3 = f3';

% 曲率、挠率
v = cross(f1,f2,2);                % 一阶导与二阶导做外积即叉乘
e = dot(f3,v,2);                   %（r',r'',r'''）混合积
c = zeros(length(T_seq),1);        % 定义矩阵c储存一阶导二阶导叉乘模长，d储存一阶导模长
d = c;
for i = 1:length(f)
    c(i) = norm(v(i,:));             % 一阶导二阶导外积的模长
    d(i) = norm(f1(i,:));            % 一阶导模长
end
k = c./(d.^3);                     % 曲率
torsion = e./c.^2;                 % 挠率

%% 画图
% 曲率图
figure
plot(k, 'r','LineWidth',2)
title('曲率图')

% 挠率图
figure
plot(torsion, 'r','LineWidth',2)
title('挠率图')

粒子群算法

该模型有三条规则：

• 避免碰撞：飞离最近的个体，以避免碰撞
• 速度一致：向目标前进，和邻近个体的平均速度保持一致
• 中心群集：向邻近个体的平均位置移动，向群体的中心运动

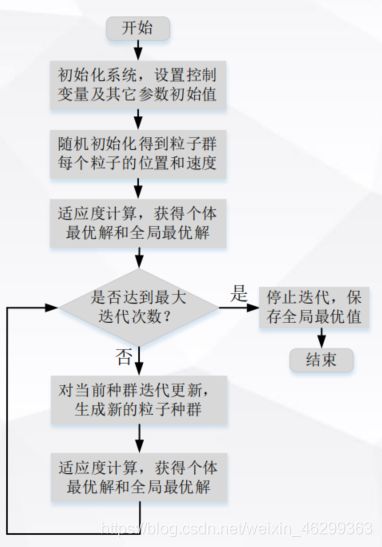
粒子群算法

• 每个寻优的问题解都被想像成一只鸟，称为“粒子”。
• 所有的粒子都由一个适应度函数（ Fitness Function ）确定适应
值以判断目前的位置好坏。
• 每一个粒子必须赋予记忆功能，能记住所搜寻到的最佳位置。
• 每一个粒子还有一个速度以决定飞行的距离和方向。这个速度
根据它本身的飞行经验以及同伴的飞行经验进行动态调整。

算法与三维路径规划的结合思想

◆ 根据第一讲的三维路径规划的基础知识，可以在起点和终点
之间任意设置若干个散点（即控制点），然后依据先后顺序
可以拟合得到光滑曲线，即三维路径。
◆ 为简单起见，可以在起点和终点之间设置三个散点。因此，
三维空间内的任意三个散点，再加上起点和终点就可以规划
三维路径。
◆ 总结而言，有：
• 将三个散点看成一个整体，即一个粒子；
• 将自由空间看成是每个粒子的可行域，即解空间；
• 将山峰等视为障碍物，即约束条件；
• 将三维路径的长度、平均曲率（挠率）等视为适应度函数；
◆ 故三维路径规划过程，就可以看成是众多粒子（三个散点）
在解空间内寻找最优位置的过程。

◆ 粒子位置更新表达式

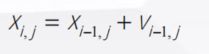
主函数
下面展示一些 内联代码片。

% 第2讲：粒子群算法
% 作者： Ally
% 日期： 2021/07/10
clc
clear
close all

%% 三维路径规划模型定义
startPos = [1, 1, 1];
goalPos = [100, 100, 80];

% 随机定义山峰地图
mapRange = [100,100,100];              % 地图长、宽、高范围
[X,Y,Z] = defMap(mapRange);

%% 初始参数设置
N = 100;           % 迭代次数
M = 50;            % 粒子数量
pointNum = 3;      % 每一个粒子包含三个位置点
w = 1.2;           % 惯性权重
c1 = 2;            % 社会权重
c2 = 2;            % 认知权重

% 粒子位置界限
posBound = [[0,0,0]',mapRange'];

% 粒子速度界限
alpha = 0.1;%粒子变化系数
%velbound 是-10到+10
velBound(:,2) = alpha*(posBound(:,2) - posBound(:,1));
velBound(:,1) = -velBound(:,2);

%% 种群初始化
% 初始化一个空的粒子结构体
particles.pos= [];
particles.v = [];
particles.fitness = [];
particles.path = [];
%个体最优
particles.Best.pos = [];
particles.Best.fitness = [];
particles.Best.path = [];

% 定义M个粒子的结构体
particles = repmat(particles,M,1);

% 初始化每一代的最优粒子，把它放成最大值
GlobalBest.fitness = inf;

% 第一代的个体粒子初始化
for i = 1:M 
    % 粒子按照unifrnd正态分布随机生成1*pointNum的随机数
    particles(i).pos.x = unifrnd(posBound(1,1),posBound(1,2),1,pointNum);
    particles(i).pos.y = unifrnd(posBound(2,1),posBound(2,2),1,pointNum);
    particles(i).pos.z = unifrnd(posBound(3,1),posBound(3,2),1,pointNum);
    
    % 初始化速度定义为0
    particles(i).v.x = zeros(1, pointNum);
    particles(i).v.y = zeros(1, pointNum);
    particles(i).v.z = zeros(1, pointNum);
    
    % 适应度 返回是否碰撞，适应度与路径
    [flag,fitness,path] = calFitness(startPos, goalPos,X,Y,Z, particles(i).pos);
    
    % 碰撞检测判断
    if flag == 1
        % 若flag=1，表明此路径将与障碍物相交，则增大适应度值
        particles(i).fitness = 1000*fitness;
        particles(i).path = path;
    else
        % 否则，表明可以选择此路径
        particles(i).fitness = fitness;
        particles(i).path = path;
    end
    
    % 更新个体粒子的最优
    particles(i).Best.pos = particles(i).pos;
    particles(i).Best.fitness = particles(i).fitness;
    particles(i).Best.path = particles(i).path;
    
    % 更新全局最优
    if particles(i).Best.fitness < GlobalBest.fitness
        GlobalBest = particles(i).Best;
    end
end

% 初始化每一代的最优适应度，用于画适应度迭代图
fitness_beat_iters = zeros(N,1);

%% 循环
for iter = 1:N
    for i = 1:M  
        % 更新速度
        particles(i).v.x = w*particles(i).v.x ...
            + c1*rand([1,pointNum]).*(particles(i).Best.pos.x-particles(i).pos.x) ...
            + c2*rand([1,pointNum]).*(GlobalBest.pos.x-particles(i).pos.x);
        particles(i).v.y = w*particles(i).v.y ...
            + c1*rand([1,pointNum]).*(particles(i).Best.pos.y-particles(i).pos.y) ...
            + c2*rand([1,pointNum]).*(GlobalBest.pos.y-particles(i).pos.y);
        particles(i).v.z = w*particles(i).v.z ...
            + c1*rand([1,pointNum]).*(particles(i).Best.pos.z-particles(i).pos.z) ...
            + c2*rand([1,pointNum]).*(GlobalBest.pos.z-particles(i).pos.z);

        % 判断是否位于速度界限以内
        particles(i).v.x = min(particles(i).v.x, velBound(1,2));
        particles(i).v.x = max(particles(i).v.x, velBound(1,1));
        particles(i).v.y = min(particles(i).v.y, velBound(2,2));
        particles(i).v.y = max(particles(i).v.y, velBound(2,1));
        particles(i).v.z = min(particles(i).v.z, velBound(3,2));
        particles(i).v.z = max(particles(i).v.z, velBound(3,1));
        
        % 更新粒子位置
        particles(i).pos.x = particles(i).pos.x + particles(i).v.x;
        particles(i).pos.y = particles(i).pos.y + particles(i).v.y;
        particles(i).pos.z = particles(i).pos.z + particles(i).v.z;

        % 判断是否位于粒子位置界限以内
        particles(i).pos.x = max(particles(i).pos.x, posBound(1,1));
        particles(i).pos.x = min(particles(i).pos.x, posBound(1,2));
        particles(i).pos.y = max(particles(i).pos.y, posBound(2,1));
        particles(i).pos.y = min(particles(i).pos.y, posBound(2,2));
        particles(i).pos.z = max(particles(i).pos.z, posBound(3,1));
        particles(i).pos.z = min(particles(i).pos.z, posBound(3,2));
        
        % 适应度计算
        [flag,fitness,path] = calFitness(startPos, goalPos,X,Y,Z, particles(i).pos);
        
        % 碰撞检测判断
        if flag == 1
            % 若flag=1，表明此路径将与障碍物相交，则增大适应度值
            particles(i).fitness = 1000*fitness;
            particles(i).path = path;
        else
            % 否则，表明可以选择此路径
            particles(i).fitness = fitness;
            particles(i).path = path;
        end
        
        % 更新个体粒子最优
        if particles(i).fitness < particles(i).Best.fitness
            particles(i).Best.pos = particles(i).pos;
            particles(i).Best.fitness = particles(i).fitness;
            particles(i).Best.path = particles(i).path;
            
            % 更新全局最优粒子
            if particles(i).Best.fitness < GlobalBest.fitness
                GlobalBest = particles(i).Best;
            end
        end
    end
    
    
    % 把每一代的最优粒子赋值给fitness_beat_iters
    fitness_beat_iters(iter) = GlobalBest.fitness;
    
    % 在命令行窗口显示每一代的信息 num2str-->num to string
    disp(['第' num2str(iter) '代:' '最优适应度 = ' num2str(fitness_beat_iters(iter))]);
    
    % 画图
    plotFigure(startPos,goalPos,X,Y,Z,GlobalBest);
    pause(0.001);
end

%% 结果展示
% 理论最小适应度：直线距离
fitness_best = norm(startPos - goalPos);
disp([ '理论最优适应度 = ' num2str(fitness_best)]);

% 画适应度迭代图
figure
plot(fitness_beat_iters,'LineWidth',2);
xlabel('迭代次数');
ylabel('最优适应度');

创建地图函数

function [X,Y,Z] = defMap(mapRange)

% 初始化地形信息
N = 10;                             % 山峰个数
peaksInfo = struct;                 % 初始化山峰特征信息结构体
peaksInfo.center = [];              % 山峰中心
peaksInfo.range = [];               % 山峰区域
peaksInfo.height = [];              % 山峰高度
peaksInfo = repmat(peaksInfo,N,1);

% 随机生成N个山峰的特征参数
for i = 1:N
    peaksInfo(i).center = [mapRange(1) * (rand*0.8+0.2), mapRange(2) * (rand*0.8+0.2)];
    peaksInfo(i).height = mapRange(3) * (rand*0.7+0.3);
    peaksInfo(i).range = mapRange*0.1*(rand*0.7+0.3);
end

% 计算山峰曲面值
peakData = [];
for x = 1:mapRange(1)
    for y = 1:mapRange(2)
        sum=0;
        for k=1:N
            h_i = peaksInfo(k).height;
            x_i = peaksInfo(k).center(1);
            y_i = peaksInfo(k).center(2);
            x_si = peaksInfo(k).range(1);
            y_si = peaksInfo(k).range(2);
            sum = sum + h_i * exp(-((x-x_i)/x_si)^2 - ((y-y_i)/y_si)^2);
        end
        peakData(x,y)=sum;
    end
end

% 构造曲面网格，用于插值判断路径是否与山峰交涉
x = [];
for i = 1:mapRange(1)
    x = [x; ones(mapRange(2),1) * i];
end
y = (1:mapRange(2))';
y = repmat(y,length(peakData(:))/length(y),1);
peakData = reshape(peakData,length(peakData(:)),1);
[X,Y,Z] = griddata(x,y,peakData,...
    linspace(min(x),max(x),100)',...
    linspace(min(y),max(y),100));
end

计算适应度,插值路线

function [flag,fitness,path] = calFitness(startPos, goalPos,X,Y,Z, pos)
%计算适应度,插值路线
% 利用三次样条拟合散点
x_seq=[startPos(1), pos.x, goalPos(1)];
y_seq=[startPos(2), pos.y, goalPos(2)];
z_seq=[startPos(3), pos.z, goalPos(3)];

k = length(x_seq);
i_seq = linspace(0,1,k);
I_seq = linspace(0,1,100);
%spline(x,y,插值个数)
X_seq = spline(i_seq,x_seq,I_seq);
Y_seq = spline(i_seq,y_seq,I_seq);
Z_seq = spline(i_seq,z_seq,I_seq);
path = [X_seq', Y_seq', Z_seq'];

% 判断生成的曲线是否与与障碍物相交
flag = 0;
for i = 2:size(path,1)
    x = path(i,1);
    y = path(i,2);
    %interp2:meshgrid 格式的二维网格数据的插值
    z_interp = interp2(X,Y,Z,x,y);
    if path(i,3) < z_interp
        flag = 1;
        break
    end
end


%% 计算三次样条得到的离散点的路径长度（适应度）
dx = diff(X_seq);
dy = diff(Y_seq);
dz = diff(Z_seq);
fitness = sum(sqrt(dx.^2 + dy.^2 + dz.^2));

画图函数

function plotFigure(startPos,goalPos,X,Y,Z, GlobalBest)

% 画起点和终点
scatter3(startPos(1), startPos(2), startPos(3),100,'bs','MarkerFaceColor','y')
hold on
scatter3(goalPos(1), goalPos(2), goalPos(3),100,'kp','MarkerFaceColor','y')

% 画山峰曲面
surf(X,Y,Z)      % 画曲面图
shading flat     % 各小曲面之间不要网格

% 画路径
path = GlobalBest.path;
pos = GlobalBest.pos;
scatter3(pos.x, pos.y, pos.z, 'go');
plot3(path(:,1), path(:,2),path(:,3), 'r','LineWidth',2);

hold off
grid on