【数据挖掘】金融风控 Task01 赛题理解

---

学习地址：https: //github.com/datawhalechina/team-learning-data-mining/tree/master/FinancialRiskControl
天池竞赛地址：https://tianchi.aliyun.com/competition/entrance/531830/introduction

---

1.赛题介绍

1.1赛题概况

比赛要求参赛选手根据给定的数据集，建立模型，预测金融风险。

赛题以预测金融风险为任务，数据集来自某信贷平台的贷款记录，总数据量超过120w，包含47列变量信息，其中15列为匿名变量。为了保证比赛的公平性，将会从中抽取80万条作为训练集，20万条作为测试集A，20万条作为测试集B，同时会对employmentTitle、purpose、postCode和title等信息进行脱敏。

---

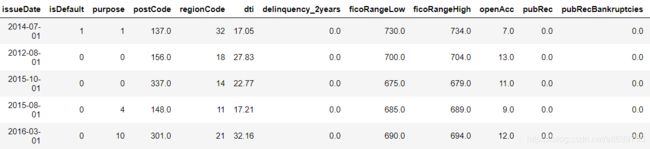
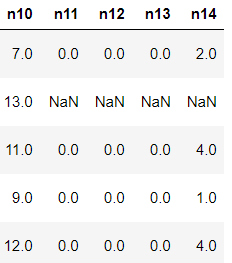
1.2 数据概况

包含47列变量信息，其中15列为匿名变量，通过info()查看数据类型及缺失情况

变量	含义	数据量及类型	备注
id	为贷款清单分配的唯一信用证标识	800000 non-null int64
loanAmnt	贷款金额	800000 non-null float64
term	贷款期限（year）	800000 non-null int64
interestRate	贷款利率	800000 non-null float64
installment	分期付款金额	800000 non-null float64
grade	贷款等级	800000 non-null object	用A、B、C、D、E、F、G表示的
subGrade	贷款等级之子级	800000 non-null object	每类有五个子类用如A1、A2…A5表示
employmentTitle	就业职称	799999 non-null float64	用数字表示
employmentLength	就业年限（年）	753201 non-null object	2 year
homeOwnership	借款人在登记时提供的房屋所有权状况	800000 non-null int64	有0、1、2、3、4、5六种
annualIncome	年收入	800000 non-null float64
verificationStatus	验证状态	800000 non-null int64	有0、1、2三种
issueDate	贷款发放的月份	800000 non-null object	2014-07-01形式
isDefault	是否违约	0或者1
purpose	借款人在贷款申请时的贷款用途类别	800000 non-null int64	0~13
postCode	借款人在贷款申请中提供的邮政编码的前3位数字	799999 non-null float64
regionCode	地区编码	800000 non-null int64
dti	债务收入比	799761 non-null float64
delinquency_2years	借款人过去2年信用档案中逾期30天以上的违约事件数	800000 non-null float64
ficoRangeLow	借款人在贷款发放时的fico所属的下限范围	800000 non-null float64
ficoRangeHigh	借款人在贷款发放时的fico所属的上限范围	800000 non-null float64
openAcc	借款人信用档案中未结信用额度的数量	800000 non-null float64
pubRec	贬损公共记录的数量	800000 non-null float64
pubRecBankruptcies	公开记录清除的数量	799595 non-null float64
revolBal	信贷周转余额合计	800000 non-null float64
revolUtil	循环额度利用率，或借款人使用的相对于所有可用循环信贷的信贷金额	799469 non-null float64
totalAcc	借款人信用档案中当前的信用额度总数	800000 non-null float64
initialListStatus	贷款的初始列表状态	800000 non-null int64	0或者1
applicationType	表明贷款是个人申请还是与两个共同借款人的联合申请	800000 non-null int64
earliesCreditLine	借款人最早报告的信用额度开立的月份	800000 non-null object	Aug-2001
title	借款人提供的贷款名称	799999 non-null float64	0或1
policyCode	公开可用的策略_代码=1新产品不公开可用的策略_代码=2	800000 non-null float64
n0		759730 non-null float64
n1		759730 non-null float64
n2		759730 non-null float64
n2.1		759730 non-null float64
n4		766761 non-null float64
n5		759730 non-null float64
n6		759730 non-null float64
n7		759730 non-null float64
n8		759729 non-null float64
n9		759730 non-null float64
n10		766761 non-null float64
n11		730248 non-null float64
n12		759730 non-null float64
n13		759730 non-null float64
n14		759730 non-null float64

---

1.3 预测指标

采用AUC作为评价指标，AUC（Area Under Curve）被定义为 ROC曲线 下与坐标轴围成的面积。

---

1.3.1 混淆矩阵

（1）若一个实例是正类，并且被预测为正类，即为真正类TP(True Positive )
（2）若一个实例是正类，但是被预测为负类，即为假负类FN(False Negative )
（3）若一个实例是负类，但是被预测为正类，即为假正类FP(False Positive )
（4）若一个实例是负类，并且被预测为负类，即为真负类TN(True Negative )
使用方法：

from sklearn.metrics import confusion_matrix#混淆矩阵
sklearn.metrics.confusion_matrix(y_true, y_pred, labels=None, sample_weight=None)
#y_true:是样本真实分类结果
#y_pred 是样本预测分类结果 
#labels是所给出的类别，通过这个可对类别进行选择 #sample_weight 是样本权重

例子

#导入相关包
import numpy as np
from sklearn.metrics import confusion_matrix#混淆矩阵
y_pred=[0,1,0,1] #预测值
y_true=[0,1,1,0] #真实值
#混淆矩阵
#真正1 真负1 假正1 假负1
print('混淆矩阵为：\n',confusion_matrix(y_true,y_pred))

---

1.3.2 准确率、精确率、召回率、F1 Score

（1）准确率（Accuracy） 准确率是常用的一个评价指标，但是不适合样本不均衡的情况，即所有预测准确的/总预测样本数。 $$Accuracy=\frac{TP+TN}{TP+TN+FP+FN}$$

（2）精确率（Precision） 又称查准率，正确预测为正样本（TP）占预测为正样本(TP+FP)的百分比。 $$Precision=\frac{TP}{TP+FP}$$

（3）召回率（Recall） 又称为查全率，正确预测为正样本（TP）占正样本(TP+FN)的百分比。 $$Recall=\frac{TP}{TP+FN}$$

（4）F1 Score 精确率和召回率是相互影响的，精确率升高则召回率下降，召回率升高则精确率下降，如果需要兼顾二者，就需要精确率、召回率的结合F1 Score。 $$F1-Score=\frac{2}{\frac{1}{Precision}+\frac{1}{Recall}}$$
使用方法

#计算准确率精确率召回率和F1分数
from sklearn import  metrics
y_pred=[0,1,0,1] #预测值
y_true=[0,1,1,0] #真实值
#准确率=预测准确的/所有预测
print('准确率为：',metrics.accuracy_score(y_true,y_pred))
#精确率=真正确的/所有预测正确的=0.5
print('精确率为：',metrics.precision_score(y_true,y_pred))
#召回率=真正确的/正样本数=0.5
print('召回率为：',metrics.recall_score(y_true,y_pred))
#F1分数=2/4=0.5
print('F1分数为：',metrics.f1_score(y_true,y_pred))

也可以使用sklearn中的classification_report函数用于显示主要分类指标的文本报告．在报告中显示每个类的精确度，召回率，F1值等信息。

使用方法

sklearn.metrics.classification_report(y_true, y_pred, labels=None, target_names=None, sample_weight=None, digits=2, output_dict=False)

参数	作用
y_true	1 维数组，真实数据的分类标签
y_pred	1 维数组，模型预测的分类标签
labels	列表，需要评估的标签名称
target_names	列表，指定标签名称
sample_weight	1 维数组，不同数据点在评估结果中所占的权重
digits	评估报告中小数点的保留位数，如果 output_dict=True，此参数不起作用，返回的数值不作处理
output_dict	若真，评估结果以字典形式返回返回字符串或者字典

例子

#精确率、召回率以及f-分数可使用classification_report模块
from sklearn.metrics import classification_report
# 精确率、召回率以及f1-score
print(classification_report(y_train,pred))

---

1.3.3 P-R曲线

P-R曲线（Precision-Recall Curve） P-R曲线是描述精确率和召回率变化的曲线，横坐标为召回率，纵坐标为精确率

#P-R曲线
import matplotlib.pyplot as plt
%matplotlib inline
#PR曲线横坐标为召回率，纵坐标为精确率
from sklearn.metrics import precision_recall_curve
y_pred = [0, 1, 1, 0, 1, 1, 0, 1, 1, 1]
y_true = [0, 1, 1, 0, 1, 0, 1, 1, 0, 1]
precision,recall,thresholds=precision_recall_curve(y_true,y_pred)
plt.plot(recall,precision)
plt.ylabel('precision')
plt.xlabel('recall')

---

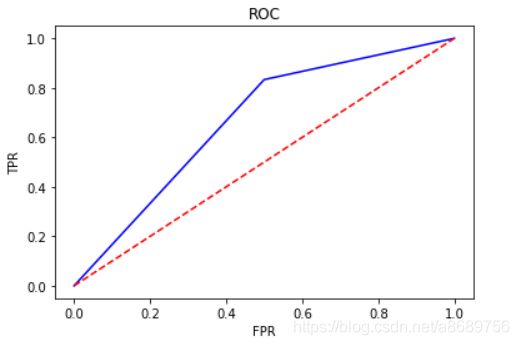
1.3.4 ROC曲线

ROC空间将假正例率（FPR）定义为 X 轴，真正例率（TPR）定义为 Y 轴。
TPR：在所有实际为正例的样本中，被正确地判断为正例之比率（也就是召回率） $$TPR=\frac{TP}{TP+FN}$$ FPR：在所有实际为负例的样本中，被错误地判断为正例之比率。 $$FPR=\frac{FP}{FP+TN}$$

• 横轴FPR:1-TNR,1-Specificity，FPR越大，预测正类中实际负类越多。

• 纵轴TPR：Sensitivity(正类覆盖率),TPR越大，预测正类中实际正类越多。
  
  使用方法
  在sklearn中sklearn.metrics.roc_curve() 函数用于绘制ROC曲线，使用前需要调用from sklearn.metrics import roc_curve模块

参数	作用
y_true	真实的样本标签，默认为{0，1}或者{-1，1}。如果要设置为其它值，则 pos_label 参数要设置为特定值。例如要令样本标签为{1，2}，其中2表示正样本，则pos_label=2。
y_score	对每个样本的预测结果。
pos_label	正样本的标签。

roc_curve() 函数有3个返回值，即假阳率FPR、真阳率TPR、阈值thresholds，阈值thresholds为将预测结果scores从大到小排列的结果。这里的thresholds指的是大于等于这个阈值为正类，负责为负类。所以通过改变不同的阈值，预测结果也将发生变化

例子

##ROC曲线,横坐标FPR，纵坐标TPR
from sklearn.metrics import roc_curve
y_pred = [0, 1, 1, 0, 1, 1, 0, 1, 1, 1]
y_true = [0, 1, 1, 0, 1, 0, 1, 1, 0, 1]
FPR,TPR,thresholds=roc_curve(y_true,y_pred)
plt.title('ROC')
plt.plot(FPR,TPR,'b')
plt.plot([0,1],[0,1],'r--')
plt.ylabel('TPR')
plt.xlabel('FPR')

---

1.3.5 AUC面积

AUC(Area Under Curve) AUC（Area Under Curve）被定义为 ROC曲线 下与坐标轴围成的面积。
显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方，所以AUC的取值范围在0.5和1之间。AUC越接近1.0，检测方法真实性越高;等于0.5时，则真实性最低，无应用价值。

#计算AUC面积
import numpy as np
from sklearn.metrics import roc_auc_score
y_true = np.array([0, 0, 1, 1])
y_scores = np.array([0.1, 0.4, 0.35, 0.8])
print('AUC值为：',roc_auc_score(y_true,y_scores))

---

1.3.6 金融风控常见评估指标

KS(Kolmogorov-Smirnov) K-S曲线与ROC曲线类似，不同在于

• ROC曲线将真正例率和假正例率作为横纵轴
• K-S曲线将真正例率和假正例率都作为纵轴，横轴则由选定的阈值来充当。 公式如下： $$KS=max(TPR-FPR)$$ KS不同代表的不同情况，一般情况KS值越大，模型的区分能力越强，但是也不是越大模型效果就越好，如果KS过大，模型可能存在异常，所以当KS值过高可能需要检查模型是否过拟合。以下为KS值对应的模型情况，但此对应不是唯一的，只代表大致趋势。
• KS值<0.2,一般认为模型没有区分能力。
• KS值[0.2,0.3],模型具有一定区分能力，勉强可以接受
• KS值[0.3,0.5],模型具有较强的区分能力。
• KS值大于0.75，往往表示模型有异常。

#KS值 在实际操作时往往使用ROC曲线配合求出KS值
from sklearn.metrics import roc_curve
y_pred = [0, 1, 1, 0, 1, 1, 0, 1, 1, 1]
y_true = [0, 1, 1, 0, 1, 0, 1, 1, 1, 1]
FPR,TPR,thresholds=roc_curve(y_true, y_pred)
print(FPR)
print(TPR)
print(thresholds)
KS=abs(FPR-TPR).max()
print('KS值：',KS)

---

1.4 赛题流程

---

1.5 评分卡

什么是评分卡（信贷场景中）

• 以分数的形式来衡量风险几率的一种手段
• 对未来一段时间内违约/逾期/失联概率的预测
• 通常评分越高越安全
• 根据使用场景分为反欺诈评分卡、申请评分卡、行为评分卡、催收评分卡

评分卡开发的常用模型

• 逻辑回归
• 决策树

构建风控评分卡模型介绍（WOE/KS/ROC)

#评分卡 不是标准评分卡
def Score(prob,P0=600,PDO=20,badrate=None,goodrate=None):
    P0 = P0
    PDO = PDO
    theta0 = badrate/goodrate
    B = PDO/np.log(2)
    A = P0 + B*np.log(2*theta0)
    score = A-B*np.log(prob/(1-prob))
    return score

=====================================

课程一总结 赛题理解&基线（baseline）方案

1.金融风控相关知识

在贷款前会去填写一些信息数据，并且还有一定的历史数据，贷款违约便是根据这些进行预测，计算分数，决定是否进行借贷或投资最小化相关风险

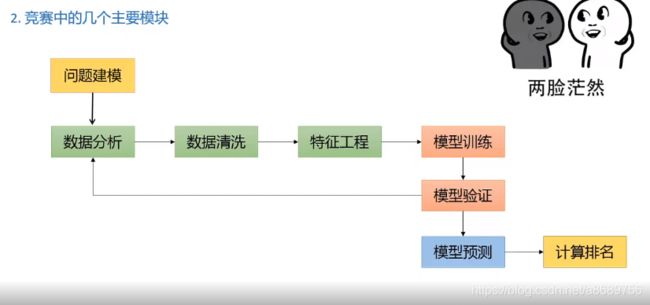
2.竞赛中主要模块

2.1 问题建模

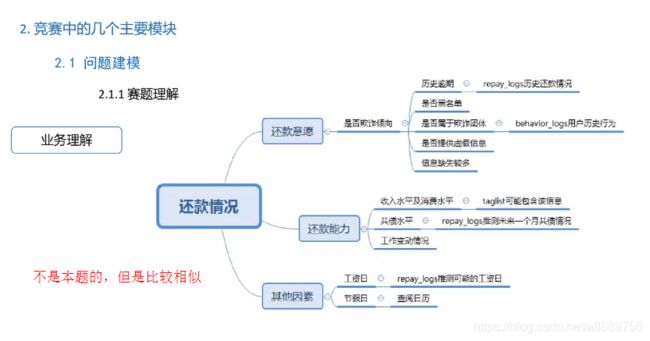
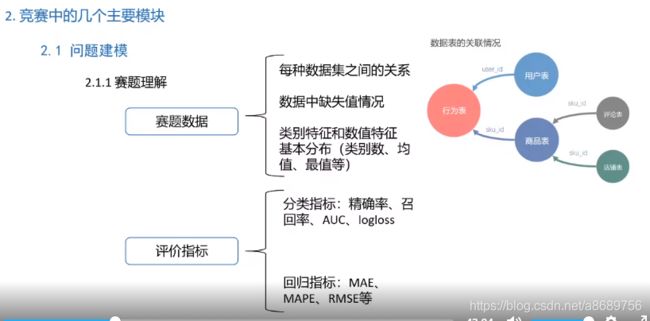
考虑是否存在实现序列，比如天气。此时可以使用时序验证

使用k折交叉验证可以使得数据更稳定些，结果更稳定些，提高泛化性

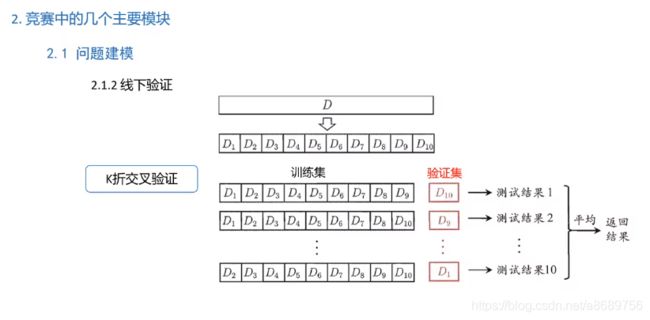
2.2 数据探索性分析（EDA）

多多尝试几类经验

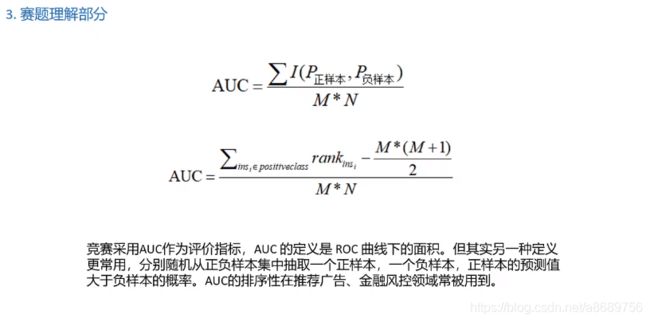
3.赛题理解部分

两个测试集替换，避免造成过拟合


查看n列先进行区分（查看哪些是正向的，哪些是负向的，避免正负相抵消）之后再做融合

更重要的是一个排序作用即正样本的值大于负样本的概率

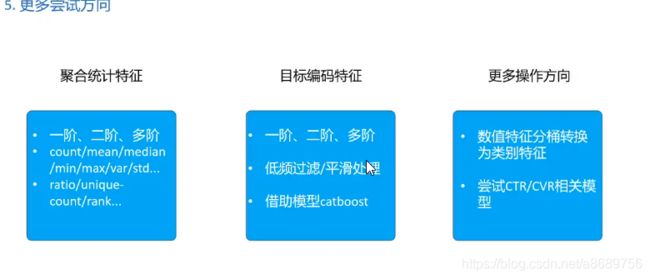
4.基线方案（baseline）

类别特征中对于高维的使用rank进行转换，使用rank更具有鲁棒性

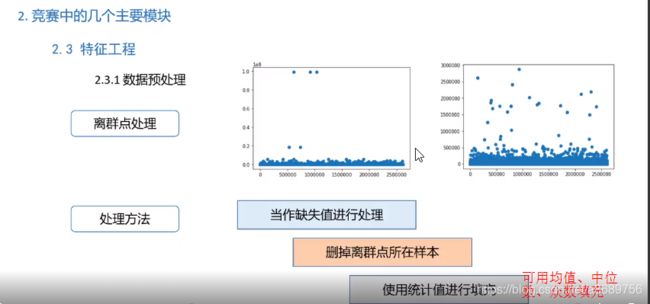
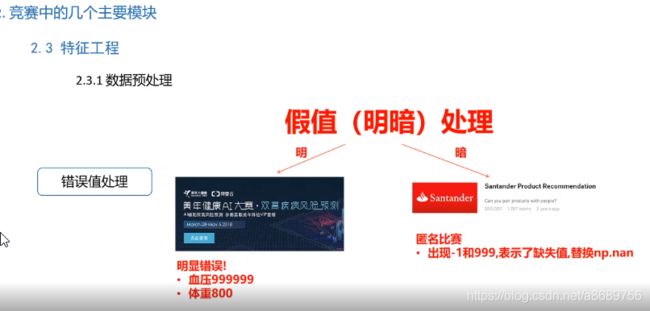
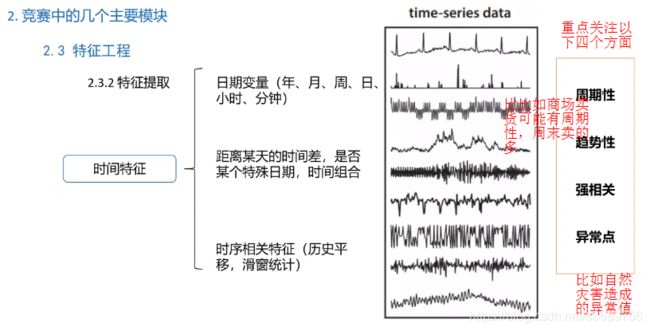
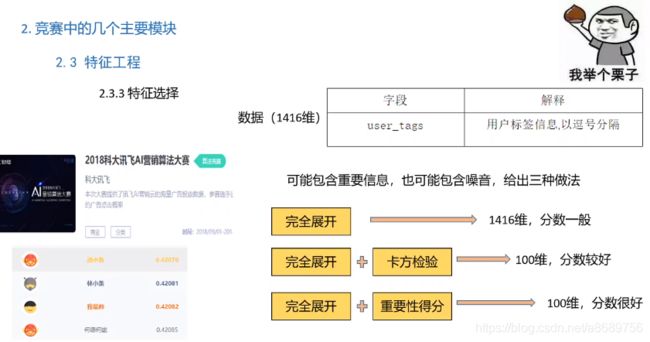
特征提取是提分的一个很好的提分项

原来的数据中职称的类别太多了，某类别可能只出现了一次其又恰好没有违约，以这个结果来判断这个职位的都不会违约是不合适的，对于这种情况可以考虑平滑处理或者用catboost来对数值特征目标特征进行编码