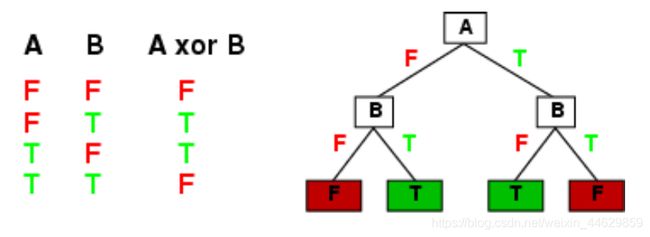
人工智能导论实验lab3(1) 分类器算法之朴素贝叶斯与决策树c++实现

实验三：分类算法实验

一．实验目的

1. ​ 巩固4种基本的分类算法的算法思想：朴素贝叶斯算法，决策树算法，人工神经网络,支持向量机；
2. ​ 能够使用现有的分类器算法代码进行分类操作
3. ​ 学习如何调节算法的参数以提高分类性能；

二、实验的硬件、软件平台

硬件：计算机

软件：操作系统：WINDOWS／Linux

应用软件：C,Java或者Matlab

三、实验内容及步骤

利用现有的分类器算法对文本数据集进行分类

实验步骤：

1．了解文本数据集的情况并阅读算法代码说明文档；

数据描述：
汽车评估数据集包含1728个数据，其中训练数据dataset.txt，测试数据集test.txt,预测数据集predict.txt。
每个数据包含6个属性，所有的数据分为4类：
Class Values: unacc, acc, good, vgood 
Attributes: 
buying: vhigh, high, med, low. 
maint: vhigh, high, med, low. 
doors: 2, 3, 4, 5more. 
persons: 2, 4, more. 
lug_boot: small, med, big. 
safety: low, med, high.

2．编写代码设计朴素贝叶斯算法，决策树算法，人工神经网络,支持向量机等分类算法，利用文本数据集中的训练数据对算法进行参数学习；

1)、朴素贝叶斯算法

• 简介

​ 贝叶斯定理用Thomas Bayes的名字命名。早在18世纪，英国学者贝叶斯提出计算条件概率的公式用来解决如下问题：

​ 假设B[1]、B[2]…B[n]互斥并且构成一个完备事件组，已知他们的概率P(B[i]),i=1,2,…,n,已知某一事件A与B相伴随机出现，并且已知条件概率P(A|B[i])的概率，求条件概率p(B[i]|A)

​ 贝叶斯定理具体形式为：

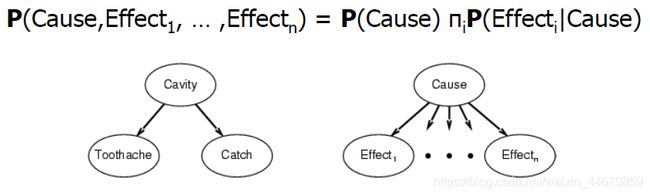
假设Cause简称B,Effect简称A

其中P(A|B)是在 B 发生的情况下 A 发生的可能性。P(B|A)是在A发生的情况下B发生的概率可能性。

​ P(A)是 A 的先验概率，之所以称为“先验”是因为它不考虑任何 B 方面的因素。P(A|B)是已知 B 发生后 A 的条件概率，也由于得自 B 的取值而被称作 A 的后验概率。P(B|A)是已知 A 发生后 B 的条件概率，也由于得自 A 的取值而被称作 B 的后验概率。P(B)是 B 的先验概率，也作标淮化常量（normalizing constant）。后验概率 = (相似度 * 先验概率)/标淮化常量，既是P(A|B) =P(AB)/P(B)，比例P(B|A)/P(B)也有时被称作标淮相似度（standardised likelihood），Bayes定理可表述为：后验概率 = 标淮相似度 * 先验概率

• 朴素贝叶斯

在数据挖掘中，朴素贝叶斯是一个比较经典的算法，给定训练数据集A,类别B，其中A

的属性列为Ai,i=1,2,…,n;B={B1,B2,…,Bn};贝叶斯算法核心思想是给定待判定数据元组，根据训练数据集进行分类预测，通过贝叶斯定理计算当前待判定元组属于某一类别的概率，概率最大者即为该待判定元组的类别归属。

​ 所谓的朴素贝叶斯是指在给定训练集数据元组中，每一个属性列之间是独立的，相互之间互不影响，A1,A2,…,An之间互相独立：

​ 通过贝叶斯公式计算后验概率：

​

此公式是表名给定元组数据A，其在A的条件下属于类别Bj的概率，由于A的每一列之间相互独立的，互不影响，因此

​

​ 在求出之后，因为P(A)对每一个类别都相同，因此可通过对的数值进行比较，因此就有：得出概率最大的即为相应的预测类别。

代码实现如下

#include
using namespace std;
struct Sample
{
    string attribute[6];
    string class_values;
};
vector data;
vector predict;
map > > count_;
map Class_Value;
string values[4] = {"unacc", "acc", "good", "vgood"};
string attribute[6] = {"buying", "maint", "doors", "persons", "lug_boot", "safety"};
void init()
{
    string attr1[3][4] = {{"vhigh", "high", "med", "low"},
                          {"vhigh", "high", "med", "low"},
                           {"2", "3", "4", "5more"}};
    string attr2[3][3] = {{"2", "4", "more"},
                          {"small", "med", "big"},
                          {"low", "med", "high"}};
    for(int i = 0; i < 4; i ++){
        Class_Value[values[i]] = 0;
        for(int j = 0; j < 6; j ++){
            if(j < 3){
                for(int k = 0; k < 4; k ++)
                    count_[values[i]][attribute[j]][attr1[j][k]] = 0;
            }else{
                for(int k = 0; k < 3; k ++)
                    count_[values[i]][attribute[j]][attr2[j - 3][k]] = 0;
            }
        }
    }
}
Sample get_Sample(string s)
{
    stringstream ss(s);
    Sample sample;
    for(int i = 0; i < 6; i ++){
        getline(ss, sample.attribute[i], ',');
    }
    getline(ss, sample.class_values, ',');
    if(sample.class_values[sample.class_values.size() - 1] == '\r')
    sample.class_values = sample.class_values.substr(0, sample.class_values.size() - 1);
    //class_values计数
    Class_Value[sample.class_values] ++;
    //属性计数
    for(int i = 0; i < 6; i ++){
        count_[sample.class_values][attribute[i]][sample.attribute[i]]++;
    }
    return sample;
}
string predict_values(Sample sample, int sum)
{
    double min = 0;
    int id = 0;
    for(int i = 0; i < 4; i ++){
        //初始P(class_values[i])
        double pre = Class_Value[values[i]] / sum;
        for(int j = 0; j < 6; j ++){
            //如果P(attribute[j], class_values[i] != 0)直接相乘/P（class_values[j])
            if(count_[values[i]][attribute[j]][sample.attribute[j]] != 0)
            pre *= (count_[values[i]][attribute[j]][sample.attribute[j]] / Class_Value[values[i]]);
            //否则分子分母都加1
            else 
              pre *= (count_[values[i]][attribute[j]][sample.attribute[j]] + 1)/ (Class_Value[values[i]] + 1);
        }
        if (min <= pre){
            id = i;
            min = pre;
        }
    }
    return values[id];
}
int main()
{
    init();
    fstream file, file2;
    file.open("test.txt", ios::in);
    file2.open("bijiao.txt", ios::out);
    string s;
    getline(file,s);
    int sum = 0;
    //输入训练集
    while(getline(file, s)){
        Sample sample = get_Sample(s);
        /*file2<

2)、决策树算法

算法思想参考博客：https://blog.csdn.net/qq_20412595/article/details/82048795（这篇博客里没有代码，代码是自己写的）

决策树简介

所谓决策树，就是一个类似于流程图的树形结构，树内部的每一个节点代表的是对一个特征的测试，树的分支代表该特征的每一个测试结果，而树的每一个叶子节点代表一个类别。树的最高层是就是根节点。

一棵决策树的生成过程主要分为以下3个部分:

• 特征选择：特征选择是指从训练数据中众多的特征中选择一个特征作为当前节点的分裂标准，如何选择特征有着很多不同量化评估标准标准，从而衍生出不同的决策树算法。
• 决策树生成： 根据选择的特征评估标准，从上至下递归地生成子节点，直到数据集不可分则停止决策树停止生长。 树结构来说，递归结构是最容易理解的方式。
• 剪枝：决策树容易过拟合，一般来需要剪枝，缩小树结构规模、缓解过拟合。剪枝技术有预剪枝和后剪枝两种。

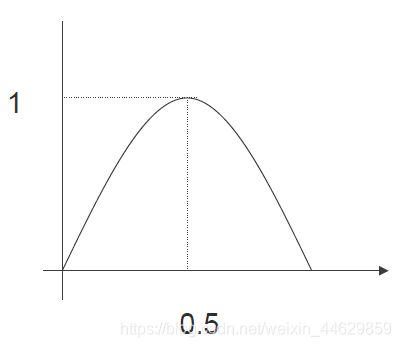
熵H(x)：衡量数据集的纯度

熵曲线

属性A的信息收益是熵的期望减少，即原有熵值-属性A 分裂后的熵值

决策树的生成

• 从根节点出发，根节点包括所有的训练样本。
• 一个节点（包括根节点），若节点内所有样本均属于同一类别，那么将该节点就成为叶节点，并将该节点标记为样本个数最多的类别。
• 否则利用采用信息增益法来选择用于对样本进行划分的特征，该特征即为测试特征，特征的每一个值都对应着从该节点产生的一个分支及被划分的一个子集。在决策树中，所有的特征均为符号值，即离散值。如果某个特征的值为连续值，那么需要先将其离散化。
• 递归上述划分子集及产生叶节点的过程，这样每一个子集都会产生一个决策（子）树，直到所有节点变成叶节点。
• 递归操作的停止条件就是：
  （1）一个节点中所有的样本均为同一类别，那么产生叶节点
  （2）没有特征可以用来对该节点样本进行划分，这里用attribute_list=null为表示。此时也强制产生叶节点，该节点的类别为样本个数最多的类别
  （3）没有样本能满足剩余特征的取值，即test_attribute= 对应的样本为空。此时也强制产生叶节点，该节点的类别为样本个数最多的类别

代码实现（只有部分，最后面会贴全部源码）

//决策树算法
struct DecesionTreeNode
{
    vector sample;//该树节点的样本
    bool is_leaf;//是否是叶子节点
    string typora;//用来决策的属性
    map child;//子样本
    string class_values;//叶节点决策出来的类或者非叶节点数量最多的类
    list attribute_list;//对于节点剩下的可选择的决策链
    mapclass_values_num;//记录样本中各个分类的数量
    double H;//原有熵值
    double IG;//记录信息增益，方便剪枝
};
double IG_min = 0, sample_num_min = 0;//阈值
mapattributeId;
map >attribute_name;//每个属性的分名称进行记录
void init2()
{
    for(int i = 0; i < 6; i ++){
        attributeId[attribute[i]] = i;
        attribute_name[attribute[i]] = vector();
        if(i < 3){
            for(int j = 0; j < 4; j ++)
                attribute_name[attribute[i]].push_back(attr1[i][j]);
        }else{
            for(int j = 0; j < 3; j ++)
                attribute_name[attribute[i]].push_back(attr2[i - 3][j]);
        }
    }
}
//统计节点样本中各分类的数量，values是一个全局数组，记录类别
void calValuesNum(DecesionTreeNode* root)
{
    for(int i = 0; i < 4; i ++)
        root->class_values_num[values[i]] = 0;
    for(auto& v: root->sample){
        root->class_values_num[v.class_values] ++;
    }
    int id = 0;
    //记录数量最多的类
    for(int i = 1; i < 4; i ++)
        if(root->class_values_num[values[i]] > root->class_values_num[values[id]])
            id = i;
    root->class_values = values[id];
    return;
}
//计算原有样本的熵
void calH(DecesionTreeNode* root)
{
    root->H = 0;
    if(root->sample.size() == 0)
        return;
    for(int i = 0; i < 4; i ++){
        if(root->class_values_num[values[i]] != 0 && root->sample.size()!= 0)
        root->H -=((root->class_values_num[values[i]] / root->sample.size()) 
                    *(log(root->class_values_num[values[i]] / root->sample.size()) / log(2)));
    }
    return ;
}
//根据typora来划分样本
void divide(DecesionTreeNode* root, string typora)
{
    //对与属性typora的每个值处理
    for(auto v:attribute_name[typora]){
        root->child[v] = new DecesionTreeNode;
        root->child[v]->attribute_list = root->attribute_list;
        root->child[v]->attribute_list.remove(typora);
    }
    for(auto v:root->sample){
        root->child[v.attribute[attributeId[typora]]]->sample.push_back(v);
    }
    //对子节点计算熵
    for(auto v:attribute_name[typora]){
        calValuesNum(root->child[v]);
        calH(root->child[v]);
    }
    //再计算root的信息增益IG;
    root->IG = root->H;
    for(auto v:attribute_name[typora]){
        //要乘1.0，不然结果会是0
        root->IG -= ((root->child[v]->sample.size() * 1.0) / (root->sample.size() * 1.0)) * (root->child[v]->H);
    }
    //cout<<"node->IG:"<IG<IG = -0x3f3f3f3f;
    string typora;
    for(auto v:root->attribute_list){
        DecesionTreeNode *node = new DecesionTreeNode;
        node->IG = 0;
        node->typora = v;
        node->attribute_list = root->attribute_list;
        node->sample = root->sample;
        calValuesNum(node);
        calH(node);
        divide(node, v);
        if(node->IG > root->IG){
            root->IG = node->IG;
            typora = v;
        }
        delete node;
    }
    root->typora = typora;
    divide(root, typora);
}   
void dfs(DecesionTreeNode* root)
{
    calValuesNum(root);
    calH(root);
    select_attribute(root);
    for(auto v:attribute_name[root->typora]){
        if(root->child[v]->attribute_list.size() == 0 || root->child[v]->IG < IG_min || root->child[v]->sample.size()<= sample_num_min){
            root->is_leaf = true;
        }else{
            dfs(root->child[v]);
        }
    }
    return ;
}
//测试集用决策树进行判断
string search_(DecesionTreeNode* root, Sample sample)
{
    if(root->is_leaf){
        return root->class_values;
    }else{
        return search_(root->child[sample.attribute[attributeId[root->typora]]], sample);
    }
}
//具体实现函数
void DecesionTree()
{
    init2();
    DecesionTreeNode* root = new DecesionTreeNode;
    root->sample = data;
    root->is_leaf = false;
    list attribute_list(attribute, attribute + 6);
    root->attribute_list = attribute_list;
    dfs(root);//递归建树
    double suceess = 0;
    for(auto v:predict){
        string pre = search_(root, v);
        if(pre == v.class_values)
            suceess ++;
    }
    cout<<"决策树算法测试正确率："<

四、思考题

如何在参数学习或者其他方面提高算法的分类性能？

1）、贝叶斯算法优化

因为可能存在一些类别某种属性为0，使得这时相乘出来的概率P为0，这时可以分子分母同时加1，避免了0的出现。

2）、决策树算法

因为决策树算法可能导致过拟合，所以可以用剪枝来优化，比如预剪枝和后剪枝，具体实现在算法思路里提了，还可以用上课提到的χ2剪枝

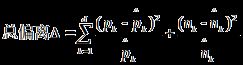
Δ值的分布是d-1个自由度的χ2分布,d是属性可取值的个数
Δ越大，拒绝的可能性越小
e.g.对于三个自由度的测试， Δ=7.82将以5%的量级拒绝， Δ=11.35将以1%的量级拒绝

源码1(朴素贝叶斯与决策树)

#include
using namespace std;
struct Sample
{
    string attribute[6];
    string class_values;
};
vector data;
vector predict;
map > > count_;
map Class_Value;
string values[4] = {"unacc", "acc", "good", "vgood"};
string attribute[6] = {"buying", "maint", "doors", "persons", "lug_boot", "safety"};
    string attr1[3][4] = {{"vhigh", "high", "med", "low"},
                          {"vhigh", "high", "med", "low"},
                           {"2", "3", "4", "5more"}};
    string attr2[3][3] = {{"2", "4", "more"},
                          {"small", "med", "big"},
                          {"low", "med", "high"}};
void init()
{
    for(int i = 0; i < 4; i ++){
        Class_Value[values[i]] = 0;
        for(int j = 0; j < 6; j ++){
            if(j < 3){
                for(int k = 0; k < 4; k ++)
                    count_[values[i]][attribute[j]][attr1[j][k]] = 0;
            }else{
                for(int k = 0; k < 3; k ++)
                    count_[values[i]][attribute[j]][attr2[j - 3][k]] = 0;
            }
        }
    }
}
Sample get_Sample(string s)
{
    stringstream ss(s);
    Sample sample;
    for(int i = 0; i < 6; i ++){
        getline(ss, sample.attribute[i], ',');
    }
    getline(ss, sample.class_values, ',');
    if(sample.class_values[sample.class_values.size() - 1] == '\r')
    sample.class_values = sample.class_values.substr(0, sample.class_values.size() - 1);
    //class_values计数
    Class_Value[sample.class_values] ++;
    //属性计数
    for(int i = 0; i < 6; i ++){
        count_[sample.class_values][attribute[i]][sample.attribute[i]]++;
    }
    return sample;
}
string predict_values(Sample sample, int sum)
{
    double min = 0;
    int id = 0;
    for(int i = 0; i < 4; i ++){
        //初始P(class_values[i])
        double pre = Class_Value[values[i]] / sum;
        for(int j = 0; j < 6; j ++){
            //如果P(attribute[j], class_values[i] != 0)直接相乘/P（class_values[j])
            if(count_[values[i]][attribute[j]][sample.attribute[j]] != 0)
            pre *= (count_[values[i]][attribute[j]][sample.attribute[j]] / Class_Value[values[i]]);
            //否则分子分母都加1
            else 
              pre *= (count_[values[i]][attribute[j]][sample.attribute[j]] + 1)/ (Class_Value[values[i]] + 1);
        }
        if (min <= pre){
            id = i;
            min = pre;
        }
    }
    return values[id];
}

//决策树算法
struct DecesionTreeNode
{
    vector sample;//该树节点的样本
    bool is_leaf;//是否是叶子节点
    string typora;//用来决策的属性
    map child;//子样本
    string class_values;//叶节点决策出来的类或者非叶节点数量最多的类
    list attribute_list;//对于节点剩下的可选择的决策链
    mapclass_values_num;//记录样本中各个分类的数量
    double H;//原有熵值
    double IG;//记录信息增益，方便剪枝
};
double IG_min = 0, sample_num_min = 0;//阈值
mapattributeId;
map >attribute_name;//每个属性的分名称进行记录
void init2()
{
    for(int i = 0; i < 6; i ++){
        attributeId[attribute[i]] = i;
        attribute_name[attribute[i]] = vector();
        if(i < 3){
            for(int j = 0; j < 4; j ++)
                attribute_name[attribute[i]].push_back(attr1[i][j]);
        }else{
            for(int j = 0; j < 3; j ++)
                attribute_name[attribute[i]].push_back(attr2[i - 3][j]);
        }
    }
}
//统计节点样本中各分类的数量，values是一个全局数组，记录类别
void calValuesNum(DecesionTreeNode* root)
{
    for(int i = 0; i < 4; i ++)
        root->class_values_num[values[i]] = 0;
    for(auto& v: root->sample){
        root->class_values_num[v.class_values] ++;
    }
    int id = 0;
    //记录数量最多的类
    for(int i = 1; i < 4; i ++)
        if(root->class_values_num[values[i]] > root->class_values_num[values[id]])
            id = i;
    root->class_values = values[id];
    return;
}
//计算原有样本的熵
void calH(DecesionTreeNode* root)
{
    root->H = 0;
    if(root->sample.size() == 0)
        return;
    for(int i = 0; i < 4; i ++){
        if(root->class_values_num[values[i]] != 0 && root->sample.size()!= 0)
        root->H -=((root->class_values_num[values[i]] / root->sample.size()) 
                    *(log(root->class_values_num[values[i]] / root->sample.size()) / log(2)));
    }
    return ;
}
//根据typora来划分样本
void divide(DecesionTreeNode* root, string typora)
{
    //对与属性typora的每个值处理
    for(auto v:attribute_name[typora]){
        root->child[v] = new DecesionTreeNode;
        root->child[v]->attribute_list = root->attribute_list;
        root->child[v]->attribute_list.remove(typora);
    }
    for(auto v:root->sample){
        root->child[v.attribute[attributeId[typora]]]->sample.push_back(v);
    }
    //对子节点计算熵
    for(auto v:attribute_name[typora]){
        calValuesNum(root->child[v]);
        calH(root->child[v]);
    }
    //再计算root的信息增益IG;
    root->IG = root->H;
    for(auto v:attribute_name[typora]){
        //要乘1.0，不然结果会是0
        root->IG -= ((root->child[v]->sample.size() * 1.0) / (root->sample.size() * 1.0)) * (root->child[v]->H);
    }
    //cout<<"node->IG:"<IG<IG = -0x3f3f3f3f;
    string typora;
    for(auto v:root->attribute_list){
        DecesionTreeNode *node = new DecesionTreeNode;
        node->IG = 0;
        node->typora = v;
        node->attribute_list = root->attribute_list;
        node->sample = root->sample;
        calValuesNum(node);
        calH(node);
        divide(node, v);
        if(node->IG > root->IG){
            root->IG = node->IG;
            typora = v;
        }
        delete node;
    }
    root->typora = typora;
    divide(root, typora);
}   
void dfs(DecesionTreeNode* root)
{
    calValuesNum(root);
    calH(root);
    select_attribute(root);
    for(auto v:attribute_name[root->typora]){
        if(root->child[v]->attribute_list.size() == 0 || root->child[v]->IG < IG_min || root->child[v]->sample.size()<= sample_num_min){
            root->is_leaf = true;
        }else{
            dfs(root->child[v]);
        }
    }
    return ;
}
//测试集用决策树进行判断
string search_(DecesionTreeNode* root, Sample sample)
{
    if(root->is_leaf){
        return root->class_values;
    }else{
        return search_(root->child[sample.attribute[attributeId[root->typora]]], sample);
    }
}
//具体实现函数
void DecesionTree()
{
    init2();
    DecesionTreeNode* root = new DecesionTreeNode;
    root->sample = data;
    root->is_leaf = false;
    list attribute_list(attribute, attribute + 6);
    root->attribute_list = attribute_list;
    dfs(root);//递归建树
    /*for(auto v:attribute_name[root->typora]){
        cout<child[v]->H<child[v]->typora<