【青岛大学·王卓】第3章_栈和队列
【青岛大学·王卓】第3章_栈和队列
20221107-20221119
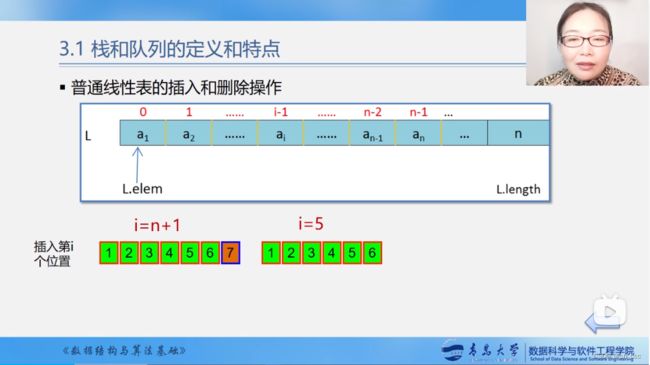
3.1 栈和队列的定义和特点
普通线性表插入和删除可以是线性表中的任意为位置；
3.1.1 栈
-
栈的概念
栈和队列是两种常用的、重要的数据结构。栈和队列是限定插入和删除只能在表的端点进行的线性表。
- 栈特点
后进先出
- 栈的应用：
由于栈的操作具有后进先出的固有特性；使栈成为程序设计中有用的工具。另外，如果问题求解的过程具有后进先出的天然特性的话，求解的算法中必然需要利用栈。
- 常见问题
- 数制转换
- 表达式求值
- 括号匹配的检验
- 八皇后问题
- 行编辑程序
- 函数调用
- 迷宫求解
- 递归调用实现
- 栈的特点
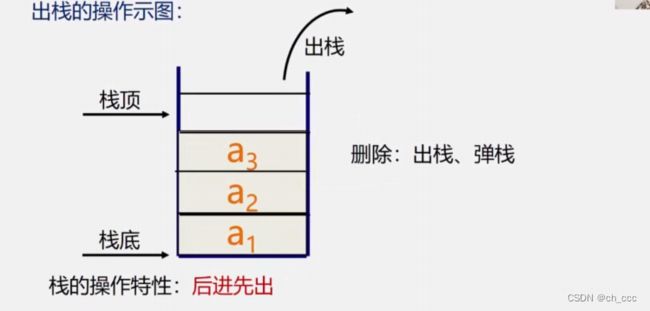
栈（Stack）是特殊的一种线性表,是限定仅在一端（通常是表尾）进行插入和删除操作的线性表；
又称**后进先出（Last In First Out）**的线性表，LIFO
- 栈的相关概念
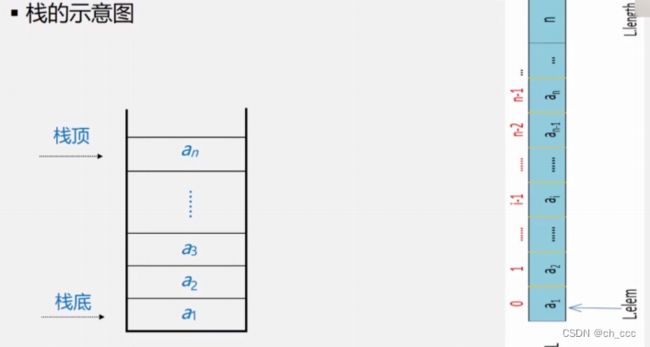
栈是仅在表尾进行插入和删除操作的线性表；
表尾 a n a_{n} an称为栈顶Top，表头 a 1 a_{1} a1称为栈底Base。例如栈： s = ( a 1 , a 2 , . . . , a n − 1 , a n ) s=(a_{1},a_{2},...,a_{n-1},a_{n}) s=(a1,a2,...,an−1,an)
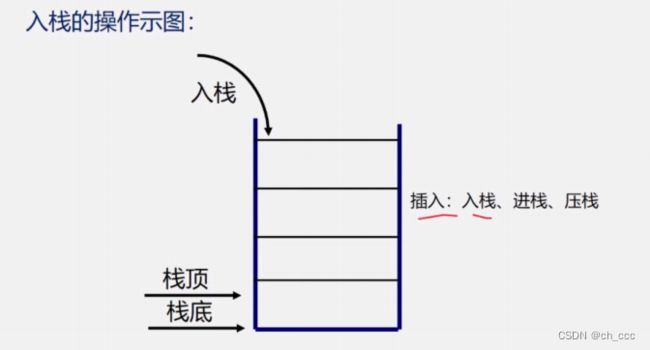
插入元素到栈顶（表尾）的操作，叫做入栈；
从栈顶（表尾）删除最后一个元素的操作，叫做出栈。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-LE9bGSRc-1671859394973)(assets/image-20221112143012509.png)]](http://img.e-com-net.com/image/info8/1b79e5ca61ab4b7a981d3622f7d0f3cb.jpg){kind=small}
- 栈示意图
- 入栈操作
- 出栈操作
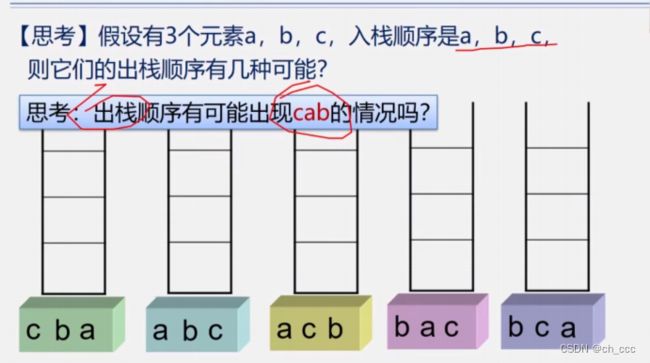
- 思考
假设有3个元素a,b,c入栈顺序abc则出栈顺序有几种可能？？
- 栈和一般线性表区别
3.1.2 队列
- 队列的概念
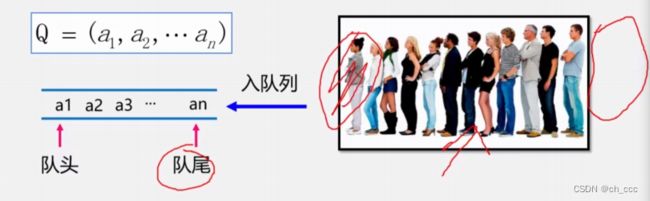
队列是一种先进先出的线性表。在表一端插入（表尾），在另一端（表头）删除。
Q = ( a 1 , a 2 , . . . , a n ) Q = (a_{1},a_{2},...,a_{n}) Q=(a1,a2,...,an)
- 队列相关概念
-
队列特点
先进先出
-
队列的常见应用
由于队列具有操作先进先出的特性，使得队列成为程序设计中求解类似排队问题的有效工具；
- 脱机打印
- 多用户系统中，多个用户排成队，分时循环使用CPU和主存；
- 按用户的优先级排成多个队，每个优先级一个队列；
- 实时控制系统，信号按接收的先后顺序依次处理；
- 网络电文传输，按到达的时间先后顺序依次处理；
栈和队列是线性表的子集，是插入和删除位置受限的线性表。
- 栈的特点
3.2 案例引入
3.3 栈的表示和操作的实现
3.3.1 栈的抽象数据类型定义
ADT Stack{
数据对象：
D = {ai|ai∈ElemSet,i=1,2,3,..,n,n≥0}
数据关系：
R1 = {<ai-1,ai>|ai-1,ai∈D，i=1,2,3,..,n}
约定an端为栈顶，a1端为栈低。
基本操作：初始化，进栈、出栈、取栈顶元素等。
}ADT Stack;
3.3.2 栈的表示
由于栈本身是线性表，于是栈也有顺序存储和链式存储两种方式。
栈的顺序存储-- 顺序栈
栈的链式存储–链栈；
- 存储方式
存储方式：同一般线性表的顺序存储结构完全相同；
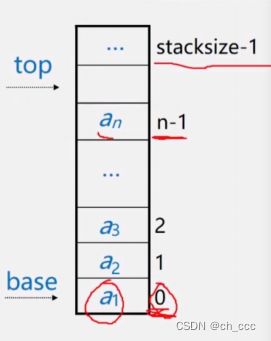
利用一组地址的连续的存储单元依次存放自栈底到栈顶的数据元素。栈底一般在低地址端。
设top指针，指示栈顶元素在顺序栈中的位置；
设base指针，指示栈底元素在顺序栈中的位置。
但是，为了方便操作通常设置top指示真正的位置的栈顶元素之上的下标地址。
另外，用stacksize表示栈可以使用的最大容量；
3.4 栈与递归
3.4.1 递归
递归：若一个对象部分地包含它自己，或者它自己给自己定义，则称为这个对象是递归的；
若一个过程间接地或间接地调用自己，称为这个过程是递归的过程。
long Fact(long n){
if(n==0){
return 1;
}
else {
return n*Fact(n-1);
}
}
什么情况使用递归方法：
- 递归定义的数学函数：N阶乘，2阶的Fibonaci数列
- 具有递归特性的数据结构：二叉树
- 可递归求解的问题；迷宫问题
递归问题-- 分治法求解
分治法：对于一个较为复杂的问题，能够分解成几个相对简单的且解法相同的或者类似的子问题来求解；
必备条件：
能将一个问题转变一个新的一个问题，而新问题与原问题的解法相同或类同，不同的仅是处理的对象，且这些处理对象是变化且有规律的。
- 可以通过上述转化而使问题简化。
- 必须有一个明确的递归出口，称为递归的边界.
void p(参数){
if (递归结束条件) 可直接求解的步骤 // 基本项
else{
p;// 归纳项
}
}
long Fact(long n){
if (n==0){ //基本项
return 1;
}
else{
return n*Fact(n-1); // 归纳项
}
}
-
递归过程
- 调用前，系统完成
- 将实参和返回地址等传递给被调用函数；
- 为被调用函数的局部变量分配存储区；
- 将控制转移到被调用函数的入口；
- 调用后，系统完成
- 保存被调用函数的计算结果；
- 释放被调用函数的数据区；
- 依照被调用函数保存的返回地址将控制转移到调用函数；
-
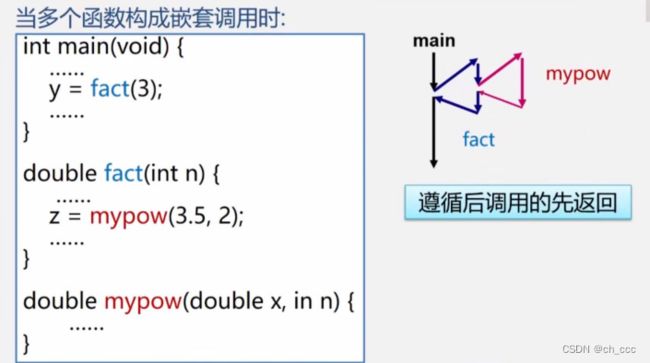
递归实例
- 实例1，多个函数嵌套调用
- 实例2:
n!
-
递归优缺点
-
优点
结构清晰，程序易读；
-
缺点
每次调用都要成圣工作记录，保存状态信息，入栈；返回时要出栈，恢复状态信息。时间开销大。
-
-
替代递归的方法
- 尾递归、单项递归 -->循环结构
- 栈模拟
3.5 队列的表示和操作的实现
3.5.1 队列基础
- 队列示意
-
相关术语
- 队列（Queue）是仅在表尾进行插入操作，在表头进行删除操作的线性表。
- 表尾即 a n a_{n} an称为队尾，表头即 a 1 a_{1} a1,称为队头；
- 它是一种先进先出（FIFO）的线性表。例如
Q = ( a 1 , a 2 , . . . , a n ) Q = (a_{1},a_{2},...,a_{n}) Q=(a1,a2,...,an)
插入元素称为入队，删除元素称为出队.
队列的存储结构为链队、顺序队
- 常见的队列应用
3.5.2 队列抽象数据类型
ADT Queue{
数据对象 D = {ai|ai∈ElemSet,i=1,2,3,...,n,n≥0}
数据关系 R = {<ai-1,ai>|ai-1,ai ∈D i=2,3...,n}
基本操作:
InitQueue(&Q); 构造空队列
DestroyQueue(&Q); 条件队列Q存在，队列Q销毁
ClearQueue(&Q);条件队列Q存在，队列Q清空
QueueLength(&Q);条件队列Q存在，返回队列元素个数
GetHead(Q，&e);条件队列Q存在，获取Q队头元素e
EnQueue(&Q,e);条件队列Q存在，插入e元素
DeQueue(&Q,&e);条件队列Q存在，删除e元素
}ADT Queue;
3.5.3 循环队列-队列实现
-
队列物理存储可以用顺序存储结构，可以用链式存储结构。
队列存储的两种方式：顺序队列和链式队列；
／／ －－－－－ 队列的顺序存储结构－－－－－
#define MAXQSIZE 100 // 队列最大长度
typedef struct
｛
QElemType *base; // 存储空间基地址
int front; // 头指针
int rear; // 尾指针
) SqQueue;
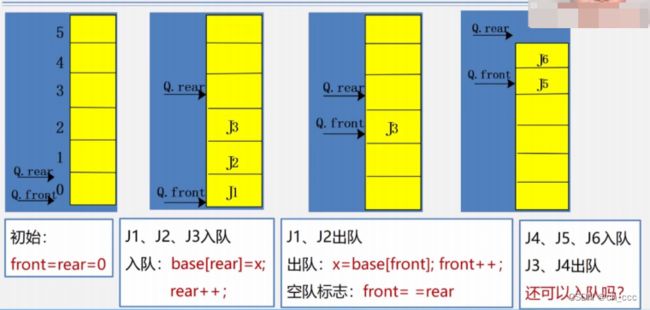
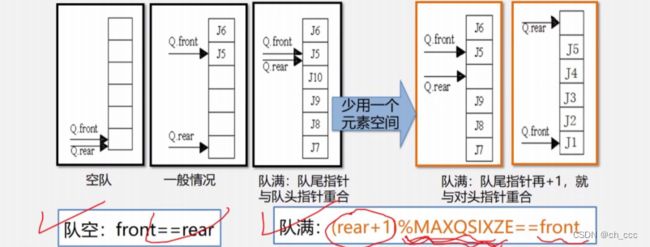
- 假溢出
解决队列假溢出：
-
将队列元素一次向队头移动。
缺点是：浪费时间，每移动一次队中元素都要移动。
-
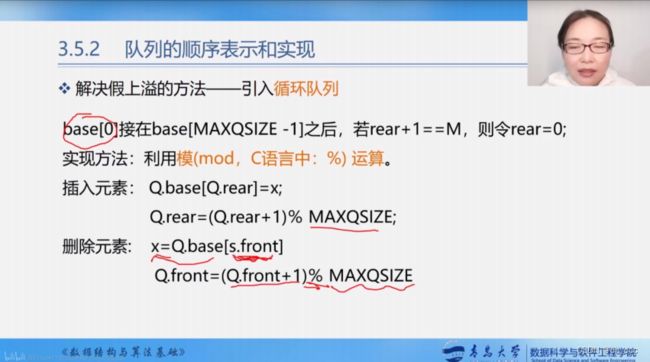
将队空间设想成循环的表，即分配给队列的m个存储单元可以循环使用。当rear为
maxqsize时，若向量的开始端空着，可以从头使用空着的空间，当front为maxqsize时也是一样。
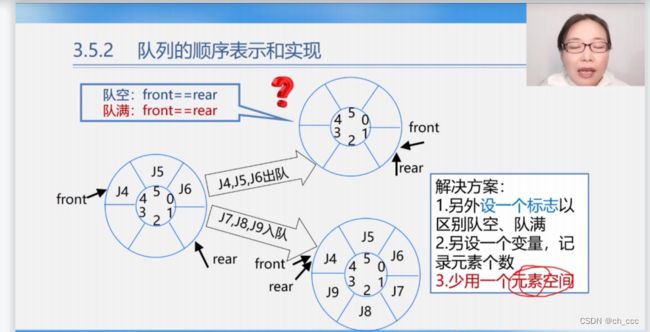
- 循环队列解决队满时判断方法：a)少用一个元素空间。b) 设置队列满的标志位
- 循环队列的类型定义
# define MAXQSIZE 100 // 队列最大长度
Typedef struct{
QElemType *base; // 初始化的动态分配存储空间
int front; // 头指针
int rear; // 尾指针
}SqQueue;
- 循环队列操作—队列初始化
Status InitQueue (SqQueue &Q)
{//构造一个空队列Q
Q.base=new QElemType[MAXQSIZE]; //为队列分配一个最大容扯为 MAXSIZE 的数组空间
if(!Q.base) exit(OVERFLOW); //存储分配失败
Q.front=Q.rear=O; //头指针和尾指针置为零， 队列为空
return OK;
}
- 循环队列操作—求队列长度
int QueueLength(SqQueue Q)
｛ // 返回Q的元素个数， 即队列的长度
return(Q.rear-Q.front+MAXQSIZE)%MAXQSIZE;
}
- 循环队列操作—循环队列入队
Status EnQueue (SqQueue &Q, QElemType e)
{// 插入元素 e 为 Q 的新的队尾元素
if ((Q. rear+l) %MAXQSIZE==Q. front){ //尾指针在循环意义上加1后等于头指针， 表明队满
return ERROR;
}
Q.base[Q.rear]=e; //新元素插入队尾
Q.rear=(Q.rear+l)%MAXQSIZE; //队尾指针加1
return OK;
}
- 循环队列操作—循环队列出队
出队操作是将队头元素删除。
Status DeQueue (SqQueue &Q, QElemType &e)
{ // 删除Q的队头元素， 用 e 返回其值
if (Q.front==Q. rear) return ERROR; // 队空
e=Q.base[Q.front]; // 保存队头元素
Q.front=(Q.front+l)%MAXQSIZE; // 队头指针加1
return OK;
}
- 循环队列操作—取队头元素
当队列非空时， 此操作返回当前队头元素的值， 队头指针保持不变。
SElemType GetHead(SqQueue Q)
{// 返回Q的队头元素，不修改队头指针
if (Q. front! =Q. rear) //队列非空
return Q.base[Q.front); // 返回队头元素的值，队头指针不变
}
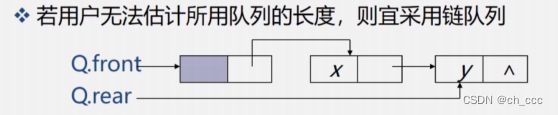
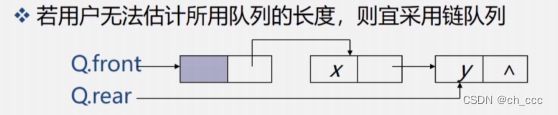
3.5.4 链队表示和实现
- 链队列的类型定义
# define MAXQSIZE 100 // 队列最大长度
Typedef struct Qnode{
QElemType data;
struct Qnode *next;
}QNode,*QueuePtr;
typedef struct{
QueuePtr front; // 队头指针
QueuePtr rear; //队尾指针
}LinkQueue;
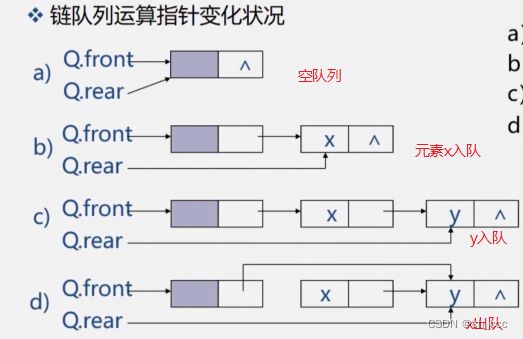
- 链队指针变化
- 链队的初始化
Status InitQueue(LinkQueue &Q){
Q.front = Q.rear = (QueuePtr)malloc(sizeof(QNode));
if(!Q.front){
exit (OVERFLOW);
}
Q.front->next = NULL;
return ok;
}
-
销毁链队列
-
链队列 元素入队
和循环队列的入队操作不同的是，链队在入队前不需要判断队是否满，需要为入队元素动态分配一个结点空间，
- 为入队元素分配节点空间，用指针p指向;
- 将新结点数据域置位e;
- 将新结点插入队尾；
- 修改队尾指针为p;
Status EnQueue (LinkQueue &Q, QElemType e)
{//插入元素e为Q的新的队尾元素
p=new QNode; //为人队元素分配结点空间，用指针p指向
p->data=e; // 将新结点数据域置为e
p->next=NULL; Q.rear->next=p; // 将新结点插入到队尾
Q.rear=p; // 修改队尾指针
return OK;
}
-
链队列 元素出队
和循环队列一样，链队在出队前也需要判断队列是否为空，不同的是，链队在出队后需要释放出队头元素的所占空间.
Status DeQueue(LinkQueue &Q,QElemType &e) {// 删除Q的队头元素， 用e返回其值 if(Q.front==Q.rear) return ERROR; // 若队列空， 则返回 ERROR p=Q.front->next; //p指向队头元素 e=p->data; //e保存队头元素的值 Q.front->next=p->next;//修改头指针 if(Q.rear==p) Q.rear=Q.front; //最后一个元素被删， 队尾指针指向头结点 delete p; //释放原队头元素的空间 return OK; } -
链队列 求队头元素
SElemType GetHead{LinkQueue Q)
{//返回Q的队头元素， 不修改队头指针
if(Q.front!=Q.rear) // 队列非空
return Q.front->next->data; // 返回队头元素的值，队头指针不变
}
3.6 案例分析与实现
3.7 脑图
3.8 感谢
感谢王卓老师