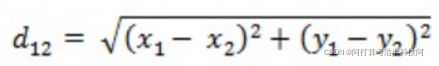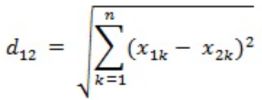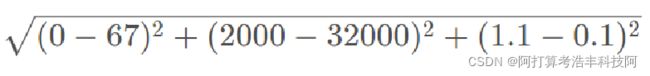3. KNN最近邻算法详解与关键技术剖析（理论篇）

一、KNN算法概述

 

K最近邻（K-Nearest-Neighbour,KNN)算法可以说是最简单的分类算法，易于理解，其核心思想就是距离的比较，即离谁最近，就被归类于谁（群体投票的方式）。

通俗解释：“近朱者赤，近墨者黑”、“物以类聚，人以群分”

生活中，其实我们也不知不觉中使用到KNN算法的例子，比如我们看待一个人，可能从一个人周围的一些人也可以看出端倪，比如平时都和什么样的人交朋友，那你也很大可能性就是这类人。

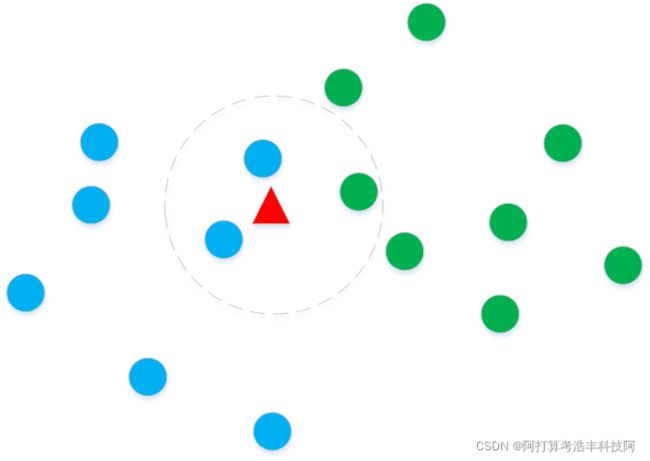
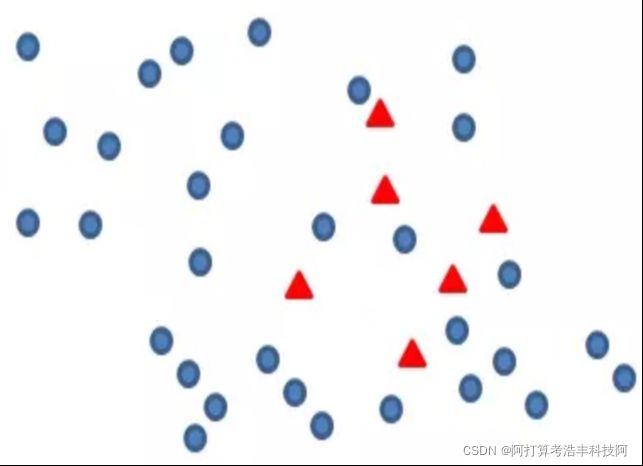
如上图所示，有蓝色圆点和绿色圆点两类样本，假设有一个新样本（红色三角形） ，希望获得其所属的类别，那我们看这个红色三角形周围3个样本，看其类别进行投票，发现有两个蓝色的圆点，一个绿色的圆点，那么我们将红色三角形这个样本划分为蓝色圆点的类别。

从上面的介绍，我们对KNN已经有了非常直观的认识。下面我们一起来看看KNN算法的方方面面。

二、KNN算法的数学基础:

K近邻算法的核心数学知识是距离的计算和权重计算。我们把需要预测的点作为中心点，然后计算其周围一定半径内的已知点距离待测样本的距离，挑选最近的TopK，进行投票，哪个类别多，该预测点就被判定属于哪一类。

距离计算

在投票之前，需要度量待测样本与空间中所有点的距离，机器学习中距离的度量通常有多种方式，比如曼哈顿距离、余弦相似度、Jaccard相似度、欧式距离等。对于KNN算法使用最多的还是欧式距离。

（1）以二维平面坐标为例，假设二维空间中有两个点A(x1,y1)和B(x2,y2)，则这两个点的欧式距离计算公式如下：

（2）如果是三维空间中的两个点，A(x1,y1,z1)和B(x2,y2,z2)，则这两个点的欧氏距离计算公式为：

 （3）推广到一般普适性，空间任意两个n维向量A(x11,x12,...,x1n)和B(x21,x22,...,x2n)，则两个点之间的欧式距离计算为：

 欧式距离的优缺点：

优点：

（1）计算简单，易于理解

（2）随着数据维度的增加，欧式距离的效果不佳，这与维度诅咒有关，在高维空间效果不佳，欧式距离对于二维或三维空间问题发挥较好。

缺点：

（1） 距离的计算会根据不同维度特征单位的选择不同而有所偏斜，这就是机器学习中对于涉及距离计算类算法存在的共性问题，即“量纲差异”。具体表现为数值较大的特征往往对欧式距离的计算结果起主导作用。

三、K最近邻算法详解

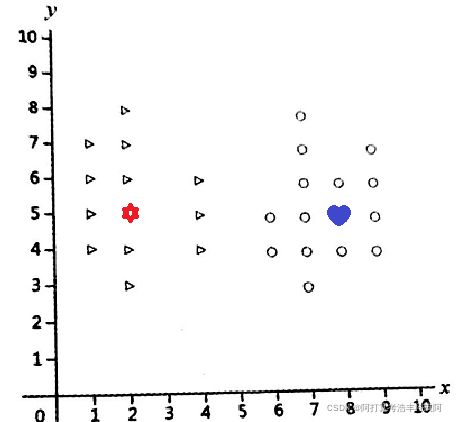
已知有两个类别的数据-三角形和圆形，如下图所示，其中三角形主要分布在坐标系左侧，而圆形主要分布在坐标系的右侧。

    

 左图为源数据在二维空间的分布图，右图为新增两个待测样本点，红色的六角形样本点(2,5)，很容易可以判定该点属于三角形的类别，因为其附近的样本全为三角形。同理对于蓝色心形样本点(8,5)，也很容易判定属于圆形的类别。

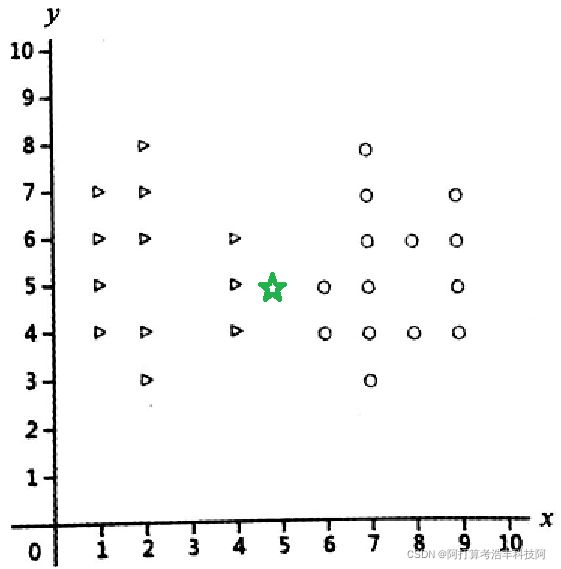
上面的例子显而易见，然而也可能会出现不好判定的情形，如下图，左图中的三角形和圆形为原样本点，对于绿色五角星新样本点（5,5），应该属于哪个类别呢？周围既有三角形，又有圆形，此时如何决策呢？

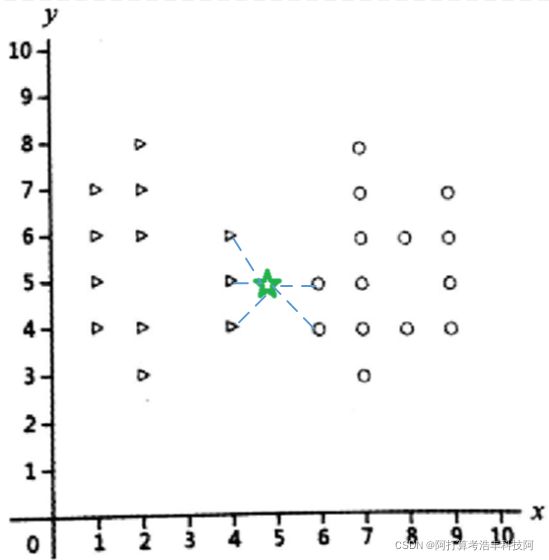
 在前文我们已经知道，K最近邻算法首先就要计算待测样本点与所有样本点之间的距离（如上面右图），然后将距离从小到大排序，取出前k个值，假设取k=5，则如下图所示，此时不难看出只剩下3个三角形和2个圆形，因此投票的结果是三角形，所以此时待测样本点被预测为三角形。

 KNN最近邻算法步骤:

（1）为判别未知样本点所属的类别，应以所有已知类别的实例作为参照

（2）选择参数K，通常不大于20，以奇数为佳

（3）计算待测样本点与所有已知类别的样本点之间的距离

（4）排序，选择最近K个已知样本点

（5）对上述K个最近邻的样本点类别进行投票，决定待测样本点所属的类别

距离加权最近邻算法

上面我们讲到KNN算法一般K值应该选择奇数，但是偶数其实也不是不可以。但是对于上面讲到的投票法来说，容易出现投票数相同的情况，会导致类别无法决定。

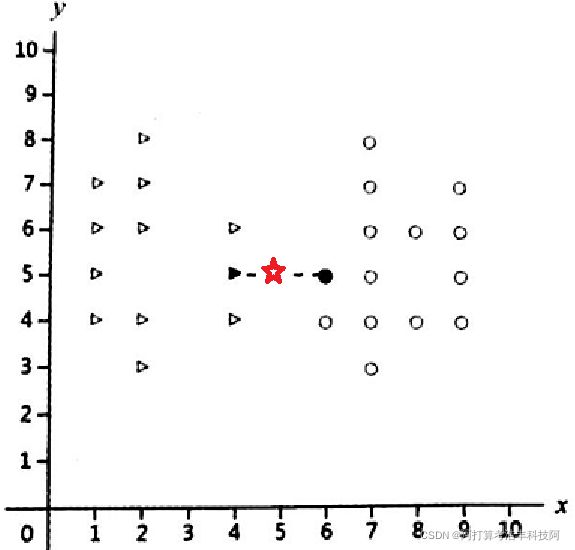
我们这里举个简单的例子来说明距离加权最近邻算法。

 假定k=2，如上图待测的红色五角星样本点坐标为(4.9,5)，到距离最近的两个点的距离分别为0.9和1.1，我们可不可以说，待测点更靠近三角形，所以待测点类别应该判定为三角形呢？

答案：完全是可以的，这其实就是距离加权最近邻算法。距离加权算法有很多种，可以根据自己的应用场景自己设定距离加权规则，本例中采用最简单的方式，即加权系数为1/d，其中d为待测点与某个类别样本点之间的距离。

因此在本例中，待测点到最近三角形距离为0.9，所以加权系数为1/0.9=1.11，而待测点到最近的圆形点为1.1，所以加权系数为1/1.1=0.91.

1.11 > 0.91，所以待测样本点被划归到三角形类别。

同理，对于K>=3的情形，待测样本点被划分到不同类别，依据加权系数进行累加求和，然后再比大小，加权系数累加和大的类别为待测样本的所属类别。

四、最近邻算法的几个关键技术问题

4.1 量纲差异

通常来说，数据可能存在多个维度，每个维度数值之间可能存在较大差异，对于存在量纲差异的数据，数值差值最大的属性对计算结果起到决定性的影响。

举个栗子：

海伦经常使用在线约会网站寻找约会对象，经过总结，发现曾交往过三种类型的人：

（1）不喜欢的人

（2）魅力一般的人

（3）极具魅力的人

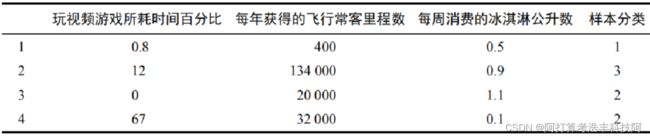
海伦从约会网站收集到的数据，共计1000条，每个样本占据一行，几列表示几个维度的特征，海伦对这几个维度都比较看重。这里截取几条数据展示。 

如果想计算样本3和4之间的距离，可以使用欧式距离：

 问题：中间的(2000-32000)的平方项对整个计算结果的影响很大吗？ 上述计算距离，KNN算法的类别选择几乎取决于飞行里程数。显然不合理，海伦认为上述几个因素都很重要。而不应该飞行里程数严重影响结果。

解决方案：

对数据进行归一化，消除量纲差异，使得各特征一视同仁。

扩展知识：距离内的算法都面临这个问题，比如kmeans算法等。另外数据归一化可以加快机器学习算法模型训练速度。

归一化： 为了消除指标之间的量纲影响，需要进行数据标准化处理，以解决数据指标之间的可比性。原始数据经过数据标准化处理后，各指标处于同一数量级，适合进行综合对比评价。

常用归一化方法：

（1）min-max标准化：

也称为离差标准化，是对原始数据的线性变换，使结果值映射到[0 ,1]之间。    

 计算公式为： x ＝ (x - min)/(max - min)

 其中，max: 样本数据的最大值； min: 样本数据的最小值

（2）Z-score标准化方法：

给予原始数据的均值（mean）和标准差（standard deviation）进行数据标准化。经过处理的数据符合标准正态分布，即均值为0，标准差为1。    

计算公式为：  x = (x - u)/σ            

其中，u: 所有样本数据的均值；    σ: 为所有样本数据的标准差

4.2 K值的选择

如何选择一个最佳的K值取决于数据？

一般情况下，K值选择的不同，可能获得完全不同的结果。

另外，在分类时较大的K值能够减小噪声的影响。但会使类别之间的界限变得模糊。如下图：

（1）K值较小，则模型复杂度较高，容易发生过拟合，学习的估计误差会增大，预测结果对近邻的实例点非常敏感。

（2）K值选择太大，模型就变得过于泛化，无法准确预测训练和测试集中的数据点，这种情况称为欠拟合。

（3）在应用中，k值一般取一个比较小的值，通常采用交叉验证法来来选取最优的K值。

（4）K值选择一个奇数，通常不超过20。

思考：K值取全量样本，还有意义吗？

 

4.3 样本不均衡问题

如果数据存在严重的不平衡，预测得出的结论往往也是有偏的，即分类结果会偏向于较多观测的类。

欠采样： 将多的那一类砍掉一部分（即欠采样），但是砍掉的数据会导致某些隐含信息的丢失。 过采样： 有放回的抽样形成的简单复制，又会使模型产生过拟合。

优化的过采样方法：在过采样的基础上，对样本做一些优化，比如坐标加一些扰动，具体地可以增加正负5%的偏移，当然在图像处理领域有一系统数据增强的方法。这里不做赘述了。

4.4 K最近邻算法优缺点：

优点：

（1）简单，易于理解

（2）容易实现

（3）通过对K值的选择可具备噪音数据的健壮性（即对异常值不敏感）

缺点：

（1）空间复杂度高

（2）计算复杂度高

（3）样本不平衡问题

五、几个思考题巩固一下

1. 简述一下KNN算法的原理和一般步骤？

2. KNN算法中为什么要做数据归一化？

3. KNN算法如何度量距离？

4. K值选择对结果有什么影响？