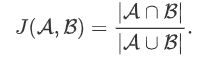DataWhale 深度学习 第三次打卡

第三次打卡学习笔记

1.批量归一化和残差网络
2.凸优化
3.梯度下降
4.目标检测
5.图像风格迁移
6.GAN和DCGAN
7.数据增强
8.模型微调

1.批量归一化和残差网络

1.1 BN算法（Batch Normalization）

为什么深度学习中要采用批量归一化？

因为神经网络学习过程本质就是为了学习数据分布，一旦训练数据与测试数据的分布不同，那么网络的泛化能力也大大降低；另外一方面，一旦每批训练数据的分布各不相同(batch 梯度下降)，那么网络就要在每次迭代都去学习适应不同的分布，这样将会大大降低网络的训练速度。

BN就像激活函数层、卷积层、全连接层、池化层一样，BN(Batch Normalization)也属于网络的一层。

BN的本质原理：在网络的每一层输入的时候，又插入了一个归一化层，也就是先做一个归一化处理（归一化至：均值0、方差为1），然后再进入网络的下一层。不过文献归一化层，可不像我们想象的那么简单，它是一个可学习、有参数（γ、β）的网络层。

BN的作用：

1.改善流经网络的梯度
2.允许更大的学习率，大幅提高训练速度：
3.减少对初始化的强烈依赖
4.改善正则化策略：作为正则化的一种形式，轻微减少了对dropout的需求
5.再也不需要使用使用局部响应归一化层了，因为BN本身就是一个归一化网络层；

批量归一化即利用小批量上的均值和标准差，不断调整神经网络中间输出，从而使整个神经网络在各层的中间输出的数值更稳定。

1.2.对全连接层做批量归一化

位置：全连接层中的仿射变换和激活函数之间。
全连接：

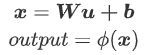
批量归一化：

这⾥ϵ > 0是个很小的常数，保证分母大于0
引入可学习参数：拉伸参数γ和偏移参数β。若批量归一化无效。

1.3.对卷积层做批量归⼀化

位置：卷积计算之后、应⽤激活函数之前。
如果卷积计算输出多个通道，我们需要对这些通道的输出分别做批量归一化，且每个通道都拥有独立的拉伸和偏移参数。 计算：对单通道，batchsize=m,卷积计算输出=pxq 对该通道中m×p×q个元素同时做批量归一化,使用相同的均值和方差。

1.4.预测时的批量归⼀化
训练：以batch为单位,对每个batch计算均值和方差。
预测：用移动平均估算整个训练数据集的样本均值和方差。

1.5残差网络（ResNet）

深度学习的问题：深度CNN网络达到一定深度后再一味地增加层数并不能带来进一步地分类性能提高，反而会招致网络收敛变得更慢，准确率也变得更差。

残差块（Residual Block）
恒等映射：
左边：f(x)=x
右边：f(x)-x=0 （易于捕捉恒等映射的细微波动）

在残差块中，输⼊可通过跨层的数据线路更快 地向前传播。

ResNet模型大体结构：

卷积(64,7x7,3)
批量一体化
最大池化(3x3,2)
残差块x4 (通过步幅为2的残差块在每个模块之间减小高和宽)
全局平均池化
全连接

稠密连接网络（DenseNet）

主要构建模块：
稠密块（dense block）： 定义了输入和输出是如何连结的。
过渡层（transition layer）：用来控制通道数，使之不过大。

2.凸优化

尽管优化方法可以最小化深度学习中的损失函数值，但本质上优化方法达到的目标与深度学习的目标并不相同。

优化方法目标：训练集损失函数值
深度学习目标：测试集损失函数值（泛化性）

2.1优化在深度学习中的挑战

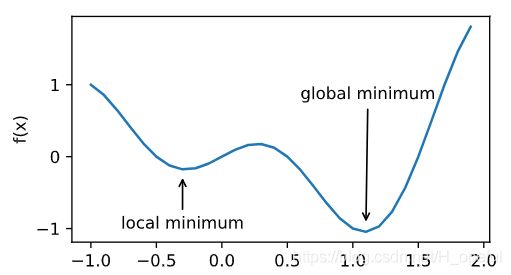
1.局部最小值

2.鞍点

3.梯度消失

2.2.凸函数性质

1.无局部极小值

2.与凸集的关系

3.二阶条件

3.梯度下降

3.1.随机梯度下降

在深度学习里，目标函数通常是训练数据集中有关各个样本的损失函数的平均。设 fi(x) 是有关索引为 i 的训练数据样本的损失函数， n 是训练数据样本数， x 是模型的参数向量，那么目标函数定义为

目标函数在 x 处的梯度计算为

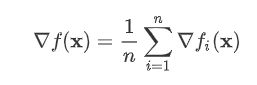
如果使用梯度下降，每次自变量迭代的计算开销为 O(n) ，它随着 n 线性增长。因此，当训练数据样本数很大时，梯度下降每次迭代的计算开销很高。

随机梯度下降（stochastic gradient descent，SGD）减少了每次迭代的计算开销。在随机梯度下降的每次迭代中，我们随机均匀采样的一个样本索引 i∈{1,…,n} ，并计算梯度 ∇fi(x) 来迭代 x ：

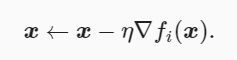
这里 η 同样是学习率。可以看到每次迭代的计算开销从梯度下降的 O(n) 降到了常数 O(1) 。值得强调的是，随机梯度 ∇fi(x) 是对梯度 ∇f(x) 的无偏估计：

这意味着，平均来说，随机梯度是对梯度的一个良好的估计。

3.2.小批量随机梯度下降

在每一次迭代中，梯度下降使用整个训练数据集来计算梯度，因此它有时也被称为批量梯度下降（batch gradient descent）。而随机梯度下降在每次迭代中只随机采样一个样本来计算梯度。正如我们在前几章中所看到的，我们还可以在每轮迭代中随机均匀采样多个样本来组成一个小批量，然后使用这个小批量来计算梯度。下面就来描述小批量随机梯度下降。

设目标函数 f(x):Rd→R 。在迭代开始前的时间步设为0。该时间步的自变量记为 x0∈Rd ，通常由随机初始化得到。在接下来的每一个时间步 t>0 中，小批量随机梯度下降随机均匀采样一个由训练数据样本索引组成的小批量 Bt 。我们可以通过重复采样（sampling with replacement）或者不重复采样（sampling without replacement）得到一个小批量中的各个样本。前者允许同一个小批量中出现重复的样本，后者则不允许如此，且更常见。对于这两者间的任一种方式，都可以使用

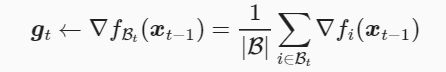
给定学习率 ηt （取正数），小批量随机梯度下降对自变量的迭代如下：

4.目标检测

真实边框

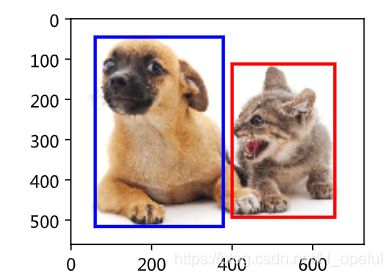
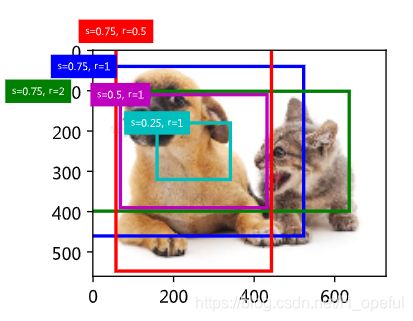
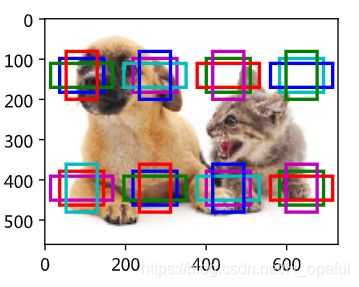
目标检测算法通常会在输入图像中采样大量的区域，然后判断这些区域中是否包含我们感兴趣的目标，并调整区域边缘从而更准确地预测目标的真实边界框（ground-truth bounding box）。不同的模型使用的区域采样方法可能不同。这里我们介绍其中的一种方法：它以每个像素为中心生成多个大小和宽高比（aspect ratio）不同的边界框。这些边界框被称为锚框（anchor box）。

4.1.生成多个锚框

假设输入图像高为h，宽为w。我们分别以图像的每个像素为中心生成不同形状的锚框。设大小为s∈(0,1]且宽高比为r>0，那么锚框的宽和高将分别为ws√r和hs/√r。当中心位置给定时，已知宽和高的锚框是确定的。

下面我们分别设定好一组大小s1,…,sn和一组宽高比r1,…,rm。如果以每个像素为中心时使用所有的大小与宽高比的组合，输入图像将一共得到whnm个锚框。虽然这些锚框可能覆盖了所有的真实边界框，但计算复杂度容易过高。因此，我们通常只对包含s1或r1的大小与宽高比的组合感兴趣，即

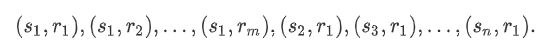
也就是说，以相同像素为中心的锚框的数量为n+m−1。对于整个输入图像，我们将一共生成wh(n+m−1)个锚框。

4.2.交互比

我们刚刚提到某个锚框较好地覆盖了图像中的狗。如果该目标的真实边界框已知，这里的“较好”该如何量化呢？一种直观的方法是衡量锚框和真实边界框之间的相似度。我们知道，Jaccard系数（Jaccard index）可以衡量两个集合的相似度。给定集合A和B，它们的Jaccard系数即二者交集大小除以二者并集大小：

实际上，我们可以把边界框内的像素区域看成是像素的集合。如此一来，我们可以用两个边界框的像素集合的Jaccard系数衡量这两个边界框的相似度。当衡量两个边界框的相似度时，我们通常将Jaccard系数称为交并比（intersection over union，IoU），即两个边界框相交面积与相并面积之比，如图9.2所示。交并比的取值范围在0和1之间：0表示两个边界框无重合像素，1表示两个边界框相等。

4.3. 标注训练集的锚框

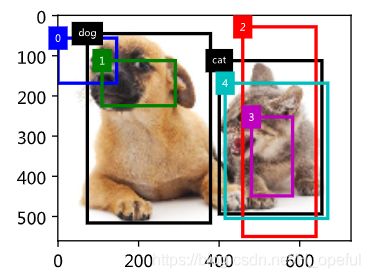
在训练集中，我们将每个锚框视为一个训练样本。为了训练目标检测模型，我们需要为每个锚框标注两类标签：一是锚框所含目标的类别，简称类别；二是真实边界框相对锚框的偏移量，简称偏移量（offset）。在目标检测时，我们首先生成多个锚框，然后为每个锚框预测类别以及偏移量，接着根据预测的偏移量调整锚框位置从而得到预测边界框，最后筛选需要输出的预测边界框。

我们知道，在目标检测的训练集中，每个图像已标注了真实边界框的位置以及所含目标的类别。在生成锚框之后，我们主要依据与锚框相似的真实边界框的位置和类别信息为锚框标注。那么，该如何为锚框分配与其相似的真实边界框呢？

假设图像中锚框分别为 A1,A2,…,Ana ，真实边界框分别为 B1,B2,…,Bnb ，且 na≥nb 。定义矩阵 X∈Rna×nb ，其中第 i 行第 j 列的元素 xij 为锚框 Ai 与真实边界框 Bj 的交并比。 首先，我们找出矩阵 X 中最大元素，并将该元素的行索引与列索引分别记为 i1,j1 。我们为锚框 Ai1 分配真实边界框 Bj1 。显然，锚框 Ai1 和真实边界框 Bj1 在所有的“锚框—真实边界框”的配对中相似度最高。接下来，将矩阵 X 中第 i1 行和第 j1 列上的所有元素丢弃。找出矩阵 X 中剩余的最大元素，并将该元素的行索引与列索引分别记为 i2,j2 。我们为锚框 Ai2 分配真实边界框 Bj2 ，再将矩阵 X 中第 i2 行和第 j2 列上的所有元素丢弃。此时矩阵 X 中已有两行两列的元素被丢弃。 依此类推，直到矩阵 X 中所有 nb 列元素全部被丢弃。这个时候，我们已为 nb 个锚框各分配了一个真实边界框。 接下来，我们只遍历剩余的 na−nb 个锚框：给定其中的锚框 Ai ，根据矩阵 X 的第 i 行找到与 Ai 交并比最大的真实边界框 Bj ，且只有当该交并比大于预先设定的阈值时，才为锚框 Ai 分配真实边界框 Bj 。

如下图所示，假设矩阵 X 中最大值为 x23 ，我们将为锚框 A2 分配真实边界框 B3 。然后，丢弃矩阵中第2行和第3列的所有元素，找出剩余阴影部分的最大元素 x71 ，为锚框 A7 分配真实边界框 B1 。接着如图9.3（中）所示，丢弃矩阵中第7行和第1列的所有元素，找出剩余阴影部分的最大元素 x54 ，为锚框 A5 分配真实边界框 B4 。最后如图9.3（右）所示，丢弃矩阵中第5行和第4列的所有元素，找出剩余阴影部分的最大元素 x92 ，为锚框 A9 分配真实边界框 B2 。之后，我们只需遍历除去 A2,A5,A7,A9 的剩余锚框，并根据阈值判断是否为剩余锚框分配真实边界框。

现在我们可以标注锚框的类别和偏移量了。如果一个锚框 A 被分配了真实边界框 B ，将锚框 A 的类别设为 B 的类别，并根据 B 和 A 的中心坐标的相对位置以及两个框的相对大小为锚框 A 标注偏移量。由于数据集中各个框的位置和大小各异，因此这些相对位置和相对大小通常需要一些特殊变换，才能使偏移量的分布更均匀从而更容易拟合。设锚框 A 及其被分配的真实边界框 B 的中心坐标分别为 (xa,ya) 和 (xb,yb) ， A 和 B 的宽分别为 wa 和 wb ，高分别为 ha 和 hb ，一个常用的技巧是将 A 的偏移量标注为

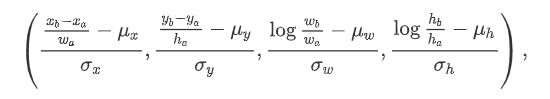
其中常数的默认值为 μx=μy=μw=μh=0,σx=σy=0.1,σw=σh=0.2 。如果一个锚框没有被分配真实边界框，我们只需将该锚框的类别设为背景。类别为背景的锚框通常被称为负类锚框，其余则被称为正类锚框。

4.4. 输出预测边界框

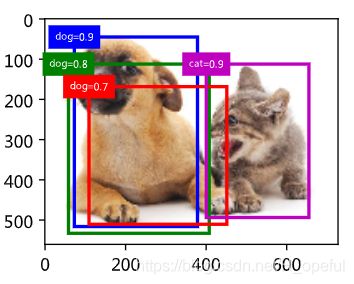
在模型预测阶段，我们先为图像生成多个锚框，并为这些锚框一一预测类别和偏移量。随后，我们根据锚框及其预测偏移量得到预测边界框。当锚框数量较多时，同一个目标上可能会输出较多相似的预测边界框。为了使结果更加简洁，我们可以移除相似的预测边界框。常用的方法叫作非极大值抑制（non-maximum suppression，NMS）。

我们来描述一下非极大值抑制的工作原理。对于一个预测边界框B，模型会计算各个类别的预测概率。设其中最大的预测概率为p，该概率所对应的类别即B的预测类别。我们也将p称为预测边界框B的置信度。在同一图像上，我们将预测类别非背景的预测边界框按置信度从高到低排序，得到列表L。从L中选取置信度最高的预测边界框B_1作为基准，将所有与B_1的交并比大于某阈值的非基准预测边界框从L中移除。这里的阈值是预先设定的超参数。此时，L保留了置信度最高的预测边界框并移除了与其相似的其他预测边界框。 接下来，从L中选取置信度第二高的预测边界框B_2作为基准，将所有与B_2的交并比大于某阈值的非基准预测边界框从L中移除。重复这一过程，直到L中所有的预测边界框都曾作为基准。此时L中任意一对预测边界框的交并比都小于阈值。最终，输出列表L中的所有预测边界框。

采用NMS之后：

4.5.多尺度目标检测

我们在实验中以输入图像的每个像素为中心生成多个锚框。这些锚框是对输入图像不同区域的采样。然而，如果以图像每个像素为中心都生成锚框，很容易生成过多锚框而造成计算量过大。举个例子，假设输入图像的高和宽分别为561像素和728像素，如果以每个像素为中心生成5个不同形状的锚框，那么一张图像上则需要标注并预测200多万个锚框（561×728×5）。

减少锚框个数并不难。一种简单的方法是在输入图像中均匀采样一小部分像素，并以采样的像素为中心生成锚框。此外，在不同尺度下，我们可以生成不同数量和不同大小的锚框。值得注意的是，较小目标比较大目标在图像上出现位置的可能性更多。举个简单的例子：形状为1×1、1×2和2×2的目标在形状为2×2的图像上可能出现的位置分别有4、2和1种。因此，当使用较小锚框来检测较小目标时，我们可以采样较多的区域；而当使用较大锚框来检测较大目标时，我们可以采样较少的区域。

5.图像风格迁移

这里我们需要两张输入图像，一张是内容图像，另一张是样式图像。

步骤：

首先，我们初始化合成图像，例如将其初始化成内容图像。该合成图像是样式迁移过程中唯一需要更新的变量，即样式迁移所需迭代的模型参数。然后，我们选择一个预训练的卷积神经网络来抽取图像的特征，其中的模型参数在训练中无须更新。深度卷积神经网络凭借多个层逐级抽取图像的特征。我们可以选择其中某些层的输出作为内容特征或样式特征。以图9.13为例，这里选取的预训练的神经网络含有3个卷积层，其中第二层输出图像的内容特征，而第一层和第三层的输出被作为图像的样式特征。接下来，我们通过正向传播（实线箭头方向）计算样式迁移的损失函数，并通过反向传播（虚线箭头方向）迭代模型参数，即不断更新合成图像。样式迁移常用的损失函数由3部分组成：内容损失（content loss）使合成图像与内容图像在内容特征上接近，样式损失（style loss）令合成图像与样式图像在样式特征上接近，而总变差损失（total variation loss）则有助于减少合成图像中的噪点。最后，当模型训练结束时，我们输出样式迁移的模型参数，即得到最终的合成图像。

总变差损失
有时候，我们学到的合成图像里面有大量高频噪点，即有特别亮或者特别暗的颗粒像素。一种常用的降噪方法是总变差降噪（total variation denoising）。假设Xij表示坐标(i,j)为的像素值，降低总变差损失

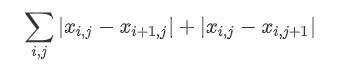
能够尽可能使邻近的像素值相似。

总结

1.样式迁移常用的损失函数由3部分组成：内容损失使合成图像与内容图像在内容特征上接近，样式损失令合成图像与样式图像在样式特征上接近，而总变差损失则有助于减少合成图像中的噪点。
2.可以通过预训练的卷积神经网络来抽取图像的特征，并通过最小化损失函数来不断更新合成图像。
3.用格拉姆矩阵表达样式层输出的样式。

6.GAN和.DCGAN

6.1.GAN

假设我们有两个网络，G（Generator）和D（Discriminator）。正如它的名字所暗示的那样，它们的功能分别是：

1.G是一个生成图片的网络，它接收一个随机的噪声z，通过这个噪声生成图片，记做G(z)。
2.D是一个判别网络，判别一张图片是不是“真实的”。它的输入参数是x，x代表一张图片，输出D（x）代表x为真实图片的概率，如果为1，就代表100%是真实的图片，而输出为0，就代表不可能是真实的图片。

在训练过程中，生成网络G的目标就是尽量生成真实的图片去欺骗判别网络D。而D的目标就是尽量把G生成的图片和真实的图片分别开来。这样，G和D构成了一个动态的“博弈过程”。

最后博弈的结果是什么？在最理想的状态下，G可以生成足以“以假乱真”的图片G(z)。对于D来说，它难以判定G生成的图片究竟是不是真实的，因此D(G(z)) = 0.5。

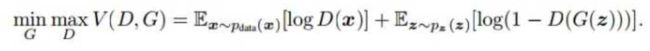
整个式子由两项构成。x表示真实图片，z表示输入G网络的噪声，而G(z)表示G网络生成的图片。
D(x)表示D网络判断真实图片是否真实的概率（因为x就是真实的，所以对于D来说，这个值越接近1越好）。而D(G(z))是D网络判断G生成的图片的是否真实的概率。

G的目的：上面提到过，D(G(z))是D网络判断G生成的图片是否真实的概率，G应该希望自己生成的图片“越接近真实越好”。也就是说，G希望D(G(z))尽可能得大，这时V(D, G)会变小。因此我们看到式子的最前面的记号是min_G。

D的目的：D的能力越强，D(x)应该越大，D(G(x))应该越小。这时V(D,G)会变大。因此式子对于D来说是求最大(max_D)

6.2.DCGAN

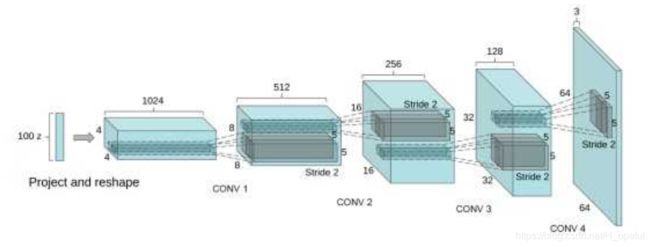
DCGAN的原理和GAN是一样的，这里就不在赘述。它只是把上述的G和D换成了两个卷积神经网络（CNN）。但不是直接换就可以了，DCGAN对卷积神经网络的结构做了一些改变，以提高样本的质量和收敛的速度。

改变为：
1.取消所有pooling层。G网络中使用转置卷积（transposed convolutional layer）进行上采样，D网络中用加入stride的卷积代替pooling。
2.在D和G中均使用batch normalization
3.去掉FC层，使网络变为全卷积网络
4.G网络中使用ReLU作为激活函数，最后一层使用tanh
5.D网络中使用LeakyReLU作为激活函数

G网结构：

7.数据增强

图像增广（image augmentation）技术通过对训练图像做一系列随机改变，来产生相似但又不同的训练样本，从而扩大训练数据集的规模。图像增广的另一种解释是，随机改变训练样本可以降低模型对某些属性的依赖，从而提高模型的泛化能力。例如，我们可以对图像进行不同方式的裁剪，使感兴趣的物体出现在不同位置，从而减轻模型对物体出现位置的依赖性。我们也可以调整亮度、色彩等因素来降低模型对色彩的敏感度。可以说，在当年AlexNet的成功中，图像增广技术功不可没。

对于一张图片：

7.1.翻转

左右翻转：

一般来讲上下翻转不如左右翻转。

7.2.裁剪

7.3.变化颜色

另一类增广方法是变化颜色。我们可以从4个方面改变图像的颜色：亮度（brightness）、对比度（contrast）、饱和度（saturation）和色调（hue）。

亮度：

对比度：

色调：

7.4.叠加多个图像增广方法

8.模型微调

假设我们想从图像中识别出不同种类的椅子，然后将购买链接推荐给用户。一种可能的方法是先找出100种常见的椅子，为每种椅子拍摄1,000张不同角度的图像，然后在收集到的图像数据集上训练一个分类模型。这个椅子数据集虽然可能比Fashion-MNIST数据集要庞大，但样本数仍然不及ImageNet数据集中样本数的十分之一。这可能会导致适用于ImageNet数据集的复杂模型在这个椅子数据集上过拟合。同时，因为数据量有限，最终训练得到的模型的精度也可能达不到实用的要求。

为了应对上述问题，一个显而易见的解决办法是收集更多的数据。然而，收集和标注数据会花费大量的时间和资金。例如，为了收集ImageNet数据集，研究人员花费了数百万美元的研究经费。虽然目前的数据采集成本已降低了不少，但其成本仍然不可忽略。

另外一种解决办法是应用迁移学习（transfer learning），将从源数据集学到的知识迁移到目标数据集上。例如，虽然ImageNet数据集的图像大多跟椅子无关，但在该数据集上训练的模型可以抽取较通用的图像特征，从而能够帮助识别边缘、纹理、形状和物体组成等。这些类似的特征对于识别椅子也可能同样有效。

微调由以下4步构成。

1.在源数据集（如ImageNet数据集）上预训练一个神经网络模型，即源模型。
2.创建一个新的神经网络模型，即目标模型。它复制了源模型上除了输出层外的所有模型设计及其参数。我们假设这些模型参数包含了源数据集上学习到的知识，且这些知识同样适用于目标数据集。我们还假设源模型的输出层跟源数据集的标签紧密相关，因此在目标模型中不予采用。
3.为目标模型添加一个输出大小为目标数据集类别个数的输出层，并随机初始化该层的模型参数。
4.在目标数据集（如椅子数据集）上训练目标模型。我们将从头训练输出层，而其余层的参数都是基于源模型的参数微调得到的。

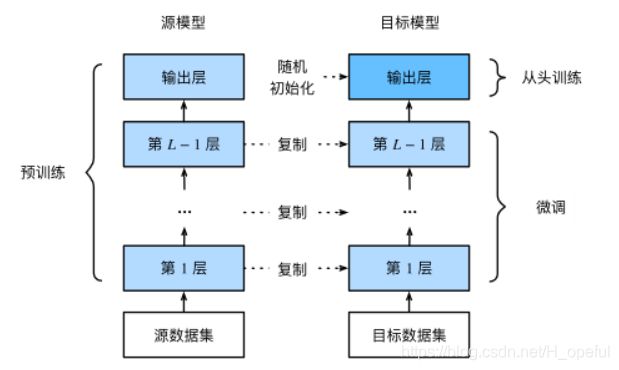
假设将ImageNet数据集上预训练的ResNet-18作为源模型。由于是在很大的ImageNet数据集上预训练的，所以参数已经足够好，因此一般只需使用较小的学习率来微调这些参数，而fc中的随机初始化参数一般需要更大的学习率从头训练。