Data-driven 3D human head reconstruction——3D人头重建笔记
数据驱动的3D人头重建
文中提出的框架可以通过一张图片重建出3D人头模型。图片首先通过卷积神经网络把图片进行分割,使用Gabor滤波器提取头发方向。之后,以标志点为约束求解FLAME面参数化模型。利用人脸图像的高频信息对细节进行增强,并利用反照率参数化模型对纹理进行补充。最后,建立了条状网格毛发数据库,并利用该数据库和图像中提取的信息,对图像中的头发进行了重建
头部重建是人体重建中较为困难的。本文主要有以下几点贡献:
- 提出一种简单快速的细节增强方法,并将增强后的细节作为法线贴图应用到人头模型,达到实时渲染的目的。
- 建立了FLAME网格的反照率参数化模型,对人头纹理进行了补充。
- 建立了一个头发-面部图像分割的数据库,并使用全卷积网络从图像中分割出头发与面部区域。
- 从发型数据集生成的条状网格数据库是实时渲染的关键。
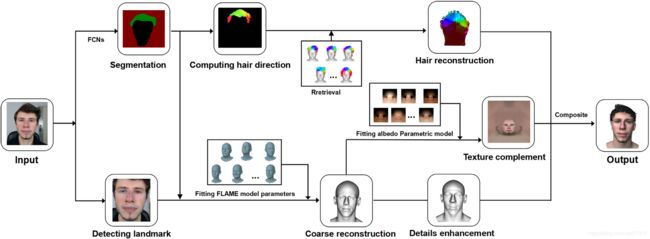
文中提出方法的处理管线图
给定一幅图像首先将其分割成头发、面部以及背景区域,计算毛发方向图并检测面部标志点;接着将FLAME面部参数模型与检测到的特征点进行匹配,得到一个粗糙的人脸网格。为捕捉更多细节使用了Z-buffer技术。文章还通过回归参数反照率模型的PCA系数,来生成完整的纹理贴图。
在头发重建阶段,通过计算多视角方向图,将头发模型数据库离线转换为网格。然后给定图像中的方向图可以从分割出的头发区域计算。通过将图像方向图与3D模型方向图进行匹配,最终可以找到3D头发网格模型。
面部与头发分割
使用全卷积网络进行学习、分类,得到分割后的图像。
面部重建
在FLAME网格上手动添加68个特征点(上图b)。把FLAME模型的3D特征点投影到2D,并尽可能接近原始图像中提取的特征点(上图a),以得到初始网格模型(上图c)
FLAME网格模型与原始图像的匹配能量可以写成
E l a n k = ∑ k = 1 68 ∥ Π ( R M k + t ) − U k ∥ + γ 1 ( w ⃗ β T β ⃗ ) 2 + γ 2 ( w ⃗ θ T θ ⃗ ) 2 + γ 3 ( w ⃗ ψ T ψ ⃗ ) 2 (1) \begin{aligned} E_{l a n k}=& \sum_{k=1}^{68}\left\|\Pi\left(R M_{k}+t\right)-U_{k}\right\|+\gamma_{1}\left(\vec{w}_{\beta}^{T} \vec{\beta}\right)^{2}+\gamma_{2}\left(\vec{w}_{\theta}^{T} \vec{\theta}\right)^{2}+\gamma_{3}\left(\vec{w}_{\psi}^{T} \vec{\psi}\right)^{2} \end{aligned} \tag{1} Elank=k=1∑68∥Π(RMk+t)−Uk∥+γ1(wβTβ)2+γ2(wθTθ)2+γ3(wψTψ)2(1)
假设相机是沿z轴方向的弱透视投影, Π = [ α 0 0 0 α 0 ] \Pi=\left[\begin{array}{lll}\alpha & 0 & 0 \\ 0 & \alpha & 0\end{array}\right] Π=[α00α00]
其中 β ⃗ , θ ⃗ , ψ ⃗ \vec{\beta},\vec{\theta},\vec{\psi} β,θ,ψ分别表示300维的形状向量、6维的姿态向量和100维的表达式参数向量,面部模型可以唯一的被这三个变量所确定。 M k = W v k ( β ⃗ , θ ⃗ , ψ ⃗ ) ∈ R 3 M_{k}=W_{v_{k}}(\vec{\beta}, \vec{\theta}, \vec{\psi}) \in R^{3} Mk=Wvk(β,θ,ψ)∈R3和 U k ∈ R 2 U_k\in R^{2} Uk∈R2分别是3D特征点和对应图像上的2D特征点。 w ⃗ β , w ⃗ θ , w ⃗ ψ \vec{w}_{\beta},\vec{w}_{\theta},\vec{w}_{\psi} wβ,wθ,wψ分别是 β ⃗ , θ ⃗ , ψ ⃗ \vec{\beta}, \vec{\theta}, \vec{\psi} β,θ,ψ的权重。 t ∈ R 3 , r ∈ R 3 × 3 t\in R^3,r\in R^{3\times3} t∈R3,r∈R3×3分别是平移向量,旋转矩阵。
使用坐标下降法通过改变 β ⃗ , θ ⃗ , ψ ⃗ , Π , R , t \vec{\beta}, \vec{\theta}, \vec{\psi},\Pi,R,t β,θ,ψ,Π,R,t,最小化式(1)直至收敛得到上图c的结果。
由于FLAME分辨率低,表达褶皱和波纹有一定困难。于是文中对FLAME做出了修改。从原始的图片中基于特征裁剪和均匀缩放生成一张512*512的图像,使用z-buff光栅化算法获得高度场曲面。由于面积细节是图像中的高频分量,那么可以在高频分量的指导下移动网格顶点。
为获得高频分量。可用顶点对图像进行采样,得到 c ( v i ) = ( r ( v i ) , g ( v i ) , b ( v i ) ) c(v_i)=(r(v_i),g(v_i),b(v_i)) c(vi)=(r(vi),g(vi),b(vi)),并计算强度 f I ( v i ) = 0.299 r ( v i ) + 0.587 g ( v i ) + 0.114 b ( v i ) f_I(v_i)=0.299r(v_i)+0.587g(v_i)+0.114b(v_i) fI(vi)=0.299r(vi)+0.587g(vi)+0.114b(vi),实际上是我们所表示网格上的标量场。而低频分量为 f l ( M ) = ( I − λ L ) − 1 f I ( M ) f_l(M)=(\bold{I}-\lambda\bold{L})^{-1}f_I(M) fl(M)=(I−λL)−1fI(M)。可通过去除低频分量获得高频分量 f h ( M ) = f I ( M ) − f l ( M ) f_h(M)=f_I(M)-f_l(M) fh(M)=fI(M)−fl(M)
在顶点向高频分向移动的过程中,为保证相邻顶点的一致性,顶点的移动距离取该顶点1邻域的平均值
d ( v ) = 1 W ∑ u ∈ N ( v ) w ( ∥ u − v ∥ ) ( 1 − ∣ ( v − u ) ⋅ n ⃗ ( v ) ∣ ∥ u − v ∥ ) ( f h ( v ) − f h ( u ) ) d(v)=\frac{1}{W} \sum_{u \in N(v)} w(\|u-v\|)\left(1-\frac{|(v-u) \cdot \vec{n}(v)|}{\|u-v\|}\right)\left(f_{h}(v)-f_{h}(u)\right) d(v)=W1u∈N(v)∑w(∥u−v∥)(1−∥u−v∥∣(v−u)⋅n(v)∣)(fh(v)−fh(u))
其中, w ( x ) = 2 ( x r ) 3 − 3 ( x r ) 2 + 1 ; 0 ≤ x < r w(x)=2\left(\frac{x}{r}\right)^{3}-3\left(\frac{x}{r}\right)^{2}+1;0 \leq x
v v v移动后的位置通过 v ′ = v + d ( v ) n ⃗ ( v ) v^{\prime}=v+d(v) \vec{n}(v) v′=v+d(v)n(v)计算得到。完成移动后进行拉普拉斯平滑得到一个具有几何细节的网格
(a)输入图像;(b)初始FLAME网格;©细化FLAME网格;(d)提取出的高度网格;(e)细节增强结果;(f)计算的法线贴图;(g)通过法线贴图和纹理的渲染结果
整个过程如上图所示。根据含有与原图相一致的几何细节的模型(上图e),计算原始FLAME网格的法线贴图,结果如上图f。最终使用FLAME网格实时渲染细节,如上图g。
FLAME网格的完整纹理贴图
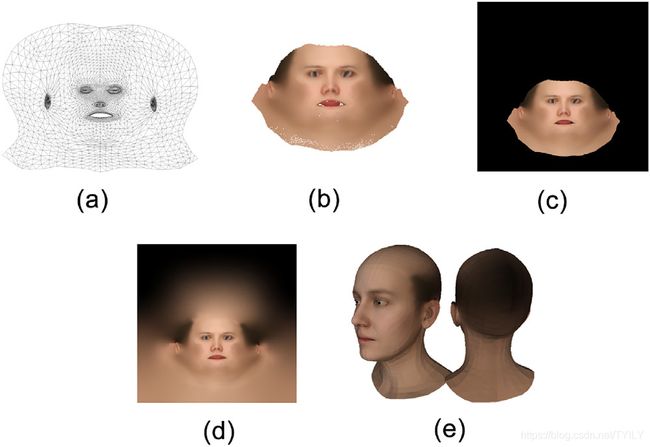
首先将FLAME参数化到平面区域(如下图a),然后将FLAME网格与BFM(巴塞尔人脸模型)网格对齐,得到无组织的纹理如下图b,通过光栅化算法渲染成纹理贴图(如下图c)。对于渲染纹理出现的瑕疵使用PULL-FILL算法修复(如下图d),最终给FLAME网格贴上纹理如下图e
在给FLAME贴反照率纹理时,首先使用FLAME反照率参数化模型计算反照率系数
min β ~ ρ ∑ ( i , j ) ∈ A v ∣ A v ∣ ∥ I i j − I i j ρ ( β ~ ρ ) ∥ + w r ∑ k = 1 ∣ β ~ ρ ∣ β ~ ρ k σ p c k (2) \min _{\tilde{\beta}_{\rho}} \sum_{(i, j) \in A_{v}}^{\left|A_{v}\right|}\left\|I_{i j}-I_{i j}^{\rho}\left(\widetilde{\beta}_{\rho}\right)\right\|+w_{r} \sum_{k=1}^{\left|\tilde{\beta}_{\rho}\right|} \frac{\tilde{\beta}_{\rho}^{k}}{\sigma_{p c}^{k}} \tag{2} β~ρmin(i,j)∈Av∑∣Av∣∥∥∥Iij−Iijρ(β ρ)∥∥∥+wrk=1∑∣β~ρ∣σpckβ~ρk(2)
A v A_v Av是带颜色的像素区域, I ρ ( β ~ ρ ) I^{\rho}\left(\widetilde{\beta}_{\rho}\right) Iρ(β ρ)是对应像素的反照率;第二项是正则项, w r w_r wr是权重。解出式(2)中的 β ~ ρ \widetilde{\beta}_{\rho} β ρ,则输入缺失的图像的完整区域反照率可以通过混合系数 I ρ ( β ~ ρ ) I^{\rho}\left(\widetilde{\beta}_{\rho}\right) Iρ(β ρ)得到,简记为 I ~ ρ \widetilde{I}_{\rho} I ρ。
假设面层材料为朗伯材料,并从照明方程中剔除镜面反射,得到了红色通道漫反射率的球谐展开式。
r i j = R ~ i j ρ ∑ n = 0 N ∑ M = − n n l n m α n Y n m ( i j ) (3) r_{i j}=\widetilde{R}_{i j}^{\rho} \sum_{n=0}^{N} \sum_{M=-n}^{n} l_{n m} \alpha_{n} Y_{n m}(i j) \tag{3} rij=R ijρn=0∑NM=−n∑nlnmαnYnm(ij)(3)
R ~ i j ρ \widetilde{R}_{i j}^{\rho} R ijρ是像素点(i,j)的红色反照值, l n m l_{nm} lnm是球谐展开系数,是只与发现方向有关的常系数。由于文中只取第一三阶球谐函数就可以表示98%的能量,所以式(3)又可化简为
r i j = R ~ i j ρ L Y ( n i j ) r_{i j}=\widetilde{R}_{i j}^{\rho} \mathbf{L} \mathbf{Y}\left(n_{i j}\right) rij=R ijρLY(nij)
其中 L = [ 1 , l x , l y , l z , l x y , l x z , l y z , l x y 2 , l z 2 ] \mathbf{L}=\left[1, l_{x}, l_{y}, l_{z}, l_{x y}, l_{x z}, l_{y z}, l_{x y 2}, l_{z 2}\right] L=[1,lx,ly,lz,lxy,lxz,lyz,lxy2,lz2]是照明系数向量, Y ( n i j ) = [ n x , n y , n z , n x , n y , n x , n z , n y , n z , n x 2 − n v 2 , 3 n z 2 − 1 ] Y(n_{ij})=\left[n_{x}, n_{y}, n_z, n_{x}, n_{y}, n_{x}, n_{z}, n_{y}, n_{z}, n_{x}^{2}-n_{v}^{2}, 3 n_{z}^{2}-1\right] Y(nij)=[nx,ny,nz,nx,ny,nx,nz,ny,nz,nx2−nv2,3nz2−1]是仅与法向方向有关的函数。
为了求出光照与反照率可以解下面的最小化方程
min l ~ , ρ ~ R ∑ ( i , j ) ∈ A v ( ∥ ρ ~ R L ~ Y ( n i j ) − I i j R ∥ 2 + w σ R ∥ ρ ~ R − R ~ i j ρ ∥ 2 ) \min _{\tilde{l}, \tilde{\rho}_{R}} \sum_{(i, j) \in A_{v}}\left(\left\|\tilde{\rho}_{R} \tilde{\mathbf{L}} Y\left(n_{i j}\right)-I_{i j}^{R}\right\|^{2}+w_{\sigma R}\left\|\tilde{\rho}_{R}-\tilde{R}_{i j}^{\rho}\right\|^{2}\right) l~,ρ~Rmin(i,j)∈Av∑(∥∥∥ρ~RL~Y(nij)−IijR∥∥∥2+wσR∥∥∥ρ~R−R~ijρ∥∥∥2)
解此方程先不考虑第二项,使用初始反照率 R ~ i j ρ \widetilde{R}_{i j}^{\rho} R ijρ作为光照系数的初始值。然后固定光照系数去解 ρ ~ R \tilde{\rho}_{R} ρ~R,由于这是个病态问题,所以把第二项当做常项, w σ R w_{\sigma R} wσR设置为1。其他的通道可以用相同的方法去解。把求解出的反照率作为最终补充完整的表面纹理。
上图展示的是该过程的求解过程:(a)输入图像;(b)提取出的有空洞的纹理;(c)经过补全的纹理;(d)在光照条件下的渲染结果
发型重建
将发束中第 i i i个采样点的坐标 p i = ( x i , y i , z i ) p_i=(x_i,y_i,z_i) pi=(xi,yi,zi)转换成球坐标系中的坐标 ( r i , θ i , ϕ i ) (r_i,\theta_i,\phi_i) (ri,θi,ϕi)。计算第 i i i个采样点的三个正交方向 E T , i = ( cos ϕ i cos θ i , cos ϕ i sin θ i , sin ϕ i ) , E N , i = ( − sin θ i , cos θ i , 0 ) , E R , i = ( sin ϕ i cos θ i , sin ϕ i sin θ i , cos ϕ i ) E_{T, i}=\left(\cos \phi_{i} \cos \theta_{i}, \cos \phi_{i} \sin \theta_{i}, \sin \phi_{i}\right), E_{N, i}=\left(-\sin \theta_{i}, \cos \theta_{i}, 0\right),E_{R, i}=\left(\sin \phi_{i} \cos \theta_{i}, \sin \phi_{i} \sin \theta_{i}, \cos\phi_{i}\right) ET,i=(cosϕicosθi,cosϕisinθi,sinϕi),EN,i=(−sinθi,cosθi,0),ER,i=(sinϕicosθi,sinϕisinθi,cosϕi)由采样点 p i p_i pi和他的三个正交方向来设置半径,生成一个螺旋圆柱形头发网格。在生成的发束网格中,如果条状网格的平面由 E T , i , E N , i E_{T,i},E_{N,i} ET,i,EN,i定义,那么条状网格的方向将会影响条状平面进而影响最终的渲染效果。如果算法不约束条形网格平面,则只能从特定的视角观察平面。如下图所示,(a)在没有约束下生成的头发网格;(b)在约束下生成的网格。
具体来说就是利用 E N , E B E_N,E_B EN,EB计算角度 θ r o t \theta_{rot} θrot并得到一个新方向 E N ′ , E B ′ E_{N}^{\prime}, \quad E_{B}^{\prime} EN′,EB′,这两个新方向依旧与 E T E_T ET相互垂直。 E B ′ E_{B}^{\prime} EB′被作为头发束平面的方向,平面的方向与发束条状网格的法向,如下图(c)。
由于发束的中心位于原点,因此每根发束的采样点的归一化坐标可以近似为采样点的方向。这就可以作为条状网格方向的约束,即条状网格的方向尽可能接近。另一方面,还需使相邻采样点之间的角度尽可能接近。这就引出下面的优化问题:
arg min { θ r o t i } = ∑ i = 1 P n ( 1 − E B i ′ ⋅ D i ) 2 + w s ∑ j ∈ N ( i ) ∥ θ rot i − θ rot j ∥ \arg \min _{\left\{\theta_{ rot}^{i}\right\}}=\sum_{i=1}^{P_{n}}\left(1-E_{B i}^{\prime} \cdot D_{i}\right)^{2}+w_{s} \sum_{j \in N(i)}\left\|\theta_{\text {rot}}^{i}-\theta_{\text {rot}}^{j}\right\| arg{θroti}min=i=1∑Pn(1−EBi′⋅Di)2+wsj∈N(i)∑∥∥∥θroti−θrotj∥∥∥
n = 100 n=100 n=100是发束网格上的采样点数; D i D_i Di是第i个采样点的归一化坐标; E B i ′ = R ( θ r o t i , E T i ) E B i E_{B i}^{\prime}=R\left(\theta_{r o t}^{i}, E_{T i}\right) E_{B i} EBi′=R(θroti,ETi)EBi是绕 E T i E_{Ti} ETi方向旋转 θ r o t i \theta^i_{rot} θroti角度; N ( i ) = { i − 1 , i + 1 } N(i)=\{i-1, i+1\} N(i)={i−1,i+1}是与第i个采样点相邻的采样点。 w s w_s ws是平滑项。
到此为止,我们就可以生成发束网格。使用K-Means算法对发束进行聚类,聚类数为100,每个类中包含的特征有头发根节点的位置、头发长度、头发方向。选择最外层的发束作为条状头发网格在每个类中的位置,发束的生成方法如上所述。生成的条状头发网格可能无法覆盖整个头部,因此搜索未覆盖区域周围的条状头发网格并将其反复复制到该区域,直到未覆盖区域的面积小于某个阈值为止。
在数据发束数据库检索上,作者希望同时使用头发形状和头发方向来进行检索。为此,首先根据仿射变换将头发模型全部统一放在一个人体模型上。然后根据模型中的特征点选择合适的边界,确定渲染图像的大小和模型在渲染图像中的位置然后使用z坐标。
z-buffer算法生成头发形状搜索图。并将整个人体进行渲染避免当头发很长的时候只渲染头部模型不满足遮挡关系的情况。为了检索与方向信息匹配的头发模型,使用表示头发方向的颜色表示生成的条状头发网格模型,然后z-buffer算法生成方向搜索图。为了加快检索速度,对于头发形状检索图,使用极坐标将以人脸为中心均匀分割渲染图像。极坐标位于极点正上方,顺时针方向。在每个间隔对头发像素大小进行计数获得一个特征向量,该向量可以用来估计头发的形状。
条状头发网格重建。首先是由特征点计算出包围盒,分割出头发部分。并将提取出的头发图案大小变换成数据库检索中用到的图像大小,然后计算特征向量,因为检索是基于特征向量的。整个过程如下图所示。
由于是使用头发形状特征向量与头发方向在数据库中检索,所以发型的相似度可以用下式计算:
D ( h s , h t ) = ∥ f h s − f h t ∥ 2 + w c 1 ∣ m h s ∩ m h t ∣ ∑ i ∈ m h s ∩ m h t ∥ m h s i − m h t i ∥ 2 D\left(h_{s}, h_{t}\right)=\left\|f_{h_{s}}-f_{h_{t}}\right\|^{2}+w_{c} \frac{1}{\left|m_{h_{s}} \cap m_{h_{t}}\right|} \sum_{i \in m_{h_{s}} \cap m_{h_{t}}}\left\|m_{h_{s}}^{i}-m_{h_{t}}^{i}\right\|^{2} D(hs,ht)=∥fhs−fht∥2+wc∣mhs∩mht∣1i∈mhs∩mht∑∥∥mhsi−mhti∥∥2
f h S , f h t f_{h_S},f_{h_t} fhS,fht分别是发型 h s , h t h_s,h_t hs,ht的形状特征向量。 m h S i , m h t i m_{h_S}^i,m_{h_t}^i mhSi,mhti分别是 h s , h t h_s,h_t hs,ht发型搜索图上的第一个像素,值为0-255。使用上式就可以计算出两个发型之间的距离,当他们足够接近就可以认为搜索完成。
头发与面部的融合过程。对于任何FLAME网格,发型都不能准确的贴在头部,因此要对头发的位置进行校正:
(a)矫正头发的整体位置:在每个条状头发网格的根 v i r o o t v^{root}_i viroot处找到FLAME人头网格最近的点 v i F L A M E v^{FLAME}_i viFLAME形成顶点集,然后计算变换矩阵使变换后的 v i r o o t v_i^{root} viroot与 v i F L A M E v_i^{FLAME} viFLAME之间的距离最小。
(b)矫正每个条状头发的位置:对于 v ~ r o o t \widetilde{v}^{root} v root中的每一个顶点 v ~ i r o o t \widetilde{v}^{root}_i v iroot,在FLAME网格头壳区域上找到最近的点 v ~ i F L A M E \widetilde{v}^{FLAME}_i v iFLAME然后计算 v ~ r o o t \widetilde{v}^{root} v root与 v ~ i F L A M E \widetilde{v}^{FLAME}_i v iFLAME之间的平移向量 t r o o t t_{root} troot。