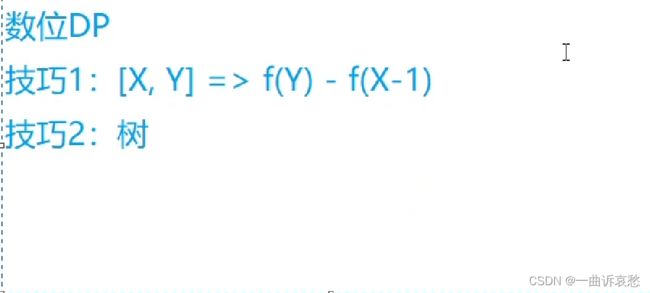数位DP深度学习及例题分析

数位DP的一般分析原则

例题分析

例题1 度的数量

只要分析从1~n拥有合法数目的数量就可以了。
假设一个位为n，那么这个位为n-1的情况下，后面所有位不管摆什么都是小于这个数的，我们只用分成两种情况，这个位等于1 ~ n-1和这个位等于n的情况，这也是数位dp的一般分析方法。
假设一个数在b进制下有n位，我们只用从最高位开始浏览，如果最高位大于等于1，我们先让答案累加这个位等于0的情况，然后再看这个数，如果这个数等于1，就保留，继续下一位，如果大于1，就直接加上这个数等于1的所有情况，然后直接break，因为大于1的数是不能保留的。

#include 
using namespace std;
const int N = 35;
int f[N][N];//放到第i位，一共有j个1的方案数
int l,r,k,b;
void init(){
	for(int i = 0;i < N;i ++)
		for(int j = 0;j <= i;j ++)
			if(!j) f[i][j] = 1;
			else f[i][j] = f[i - 1][j - 1] + f[i - 1][j];
	return;
}
int dp(int x){
	if(! x) return 0;
	vector <int> v;
	while(x){
		v.push_back(x % b);
		x = x / b;
	}
	int res = 0,last = 0;
	for(int i = v.size() - 1;i >= 0;i --){
		if(v[i]){
			res += f[i][k - last];
			if(k - last == 0) break;//如果没有1可以摆，直接break
			if(v[i] > 1){//如果大于1，直接统计这个位等于1的所有情况
				if(k - last - 1 >= 0) res += f[i][k - last - 1];
				break;
			}
			last ++;//保留1的个数加1
		}
		if(! i && k == last) res ++;//如果到最后一位，所有保留的数刚好合法，答案再加1
	}
	return res;
}
int main(){
	init();
	cin >> l >> r >> k >> b;
	cout << dp(r) - dp(l - 1);
	return 0;
}

例题2 数字游戏

用f[i][j]表示第i位且最高位为j的所有情况，很明显f[i][j] = ${\sum }_{k=j}^n$f[i-1][k]
这道题就是预处理比较难

#include 
using namespace std;
const int N = 15;
int f[N][N];//f[i][j]最高位是j,一共有i位的方案数 
void init(){
	for(int i = 0;i <= 9;i ++)
		f[1][i] = 1;
	for(int i = 2;i < N;i ++)
		for(int j = 0;j <= 9;j ++)
			for(int k = j;k <= 9;k ++)
				f[i][j] += f[i - 1][k];
}
int dp(int x){
	if(x == 0) return 1;
	vector <int> v;
	while(x){
		v.push_back(x % 10);
		x /= 10;
	}
	int last = 0,ans = 0;
	bool flag = true;
	for(int i = v.size() - 1;i >= 0;i --){
		if(flag)//如果满足不降的条件
			for(int j = last;j < v[i];j ++) 统计所有方案
				ans = ans + f[i + 1][j];
		if(v[i] >= last) last = v[i]; //计算保留的最高位
		else flag = false; //如果保留的最高位比之前保留的要低，直接break
	}
	if(flag) ans ++;//单独的情况
	return ans;
}
int main(){
	int a,b;
	init();
	while(cin >> a >> b)
		cout << dp(b) - dp(a - 1) << endl;
	return 0;
} 

例题3 windy数

跟前面的题目差不多，不过要注意前导不能为0，而前面的题目前导为不为零并没有影响，所以这道题前导为0的情况要做分类讨论，有一个点卡了挺久的，思考还要更加周全一点。

#include 
using namespace std;
const int N = 15; 
int f[N][N]; //一共有多少位,最高位是 
void init(){
	for(int i = 0;i < N;i ++)
		for(int j = 0;j <= 9;j ++){
			if(! i) f[i][j] = 1;
			else{
				for(int k = 0;k <= 9;k ++)
					if(abs(k - j) >= 2) f[i][j] += f[i - 1][k];
			}
		}
	return;
}
int dp(int x){
	if(! x) return 0;
	vector <int> v;
	while(x){
		v.push_back(x % 10);
		x = x / 10;
	}
	int ans = 0;
	bool flag = true;
	for(int i = v.size() - 2;i >= 0;i --)//单独考虑前导为0的情况
		for(int j = 1;j <= 9;j ++)
			ans = ans + f[i][j];
	for(int i = v.size() - 1;i >= 0;i --){
		if(flag){
			if(i == v.size() - 1){
				for(int j = 1;j < v[i];j ++)
					ans = ans + f[i][j];//第一位可以随便放
			}
			else{
				for(int j = 0;j < v[i];j ++)//后面放的必须满足前面的条件
					if(abs(j - v[i + 1]) >= 2) ans = ans + f[i][j];
			}
		}
		if(i != v.size() - 1 && v[i] >= v[i + 1] - 1 && v[i] <= v[i + 1] + 1){
			flag = false;
			break;
		}
	}
	if(flag) ans ++;
	return ans;
}
int main(){
	init();
	int l,r;
	scanf("%d%d",&l,&r);
	cout << dp(r) - dp(l - 1);
	return 0;
}

例题4 数字游戏 ||

数位dp主要是预处理这块特别难，其实算的地方直接套公式就好了，注意写一个取模函数防止负数，计算起来也比较方便。

#include 
using namespace std;
const int N = 100;
int f[12][N + 5][10];//分别是位数、模n余下的数、最高位是什么
int a,b,n;
int Mod(int x,int M){//取模函数
	return (x % M + M) % M;
}
void init(){
	memset(f,0,sizeof(f));
	for(int i = 0;i <= 9;i ++)
		f[1][Mod(i,n)][i] += 1;
	for(int i = 2;i < 12;i ++)
		for(int j = 0;j < n;j ++)
			for(int k = 0;k <= 9;k ++)
				for(int p = 0;p <= 9;p ++)
					f[i][j][k] += f[i - 1][Mod((j - k),n)][p];//状态继承
}
int dp(int x){
	if(x == 0) return 1;
	vector <int> v;
	while(x){
		v.push_back(x % 10);
		x = x / 10;
	}
	int ans = 0;
	int sum = 0;
	for(int i = v.size() - 1;i >= 0;i --){
		for(int k = 0;k < v[i];k ++)
			ans = ans + f[i + 1][Mod(n - sum,n)][k];
		sum += v[i];
	}
	if(sum % n == 0) ans ++;
	return ans;
}
int main(){
	while(cin >> a >> b >> n){
		init();
		printf("%d\n",dp(b) - dp(a - 1));
	}
	return 0;
}

这道题比之前的要简单，没看代码自己敲出来了，就是计算答案的时候也要考虑和上一位的联系，预处理一般是单向的，但是计算答案的时候是双向的，思考还是不周到。

#include 
using namespace std;
const int N = 11;
int f[N][10];
void init(){
	for(int i = 0;i <= 9;i ++)
		if(i != 4) f[1][i] = 1;
	for(int i = 2;i < N;i ++){
		for(int j = 0;j <= 9;j ++)
			for(int k = 0;k <= 9;k ++){
				if((j == 6 && k == 2) || (j == 4 || k == 4)) continue;
				f[i][j] += f[i - 1][k];
			}
	}
}
int dp(int x){
	if(x == 0) return 1;
	vector <int> v;
	while(x){
		v.push_back(x % 10);
		x = x / 10;
	}
	int ans = 0;
	bool flag = true;
	for(int i = v.size() - 1;i >= 0;i --){
		for(int j = 0;j < v[i];j ++)
			if(i != v.size() - 1 && v[i + 1] == 6 && j == 2) continue;
			else ans = ans + f[i + 1][j];
		if(v[i] == 4){
			flag = false;
			break;
		}
		if(i != v.size() - 1 && v[i] == 2 && v[i + 1] == 6){
			flag = false;
			break;
		} 
	}
	if(flag) ans ++;
	return ans;
}
int main(){
	init();
	int n,m;
	while(cin >> n >> m){
		if(n == 0 && m == 0) break;
		cout << dp(m) - dp(n - 1) << endl;
	}
	return 0;
}

这道题目非常变态，做了一些数位DP水题以为数位DP都很简单，这道题确实非常有难度，感觉能上银牌题的水平。
抛去平方来说其实是非常简单的，就是一些状态继承，加上平方之后，需要考虑平方之间的继承。
考虑首位为j，其他位分别为a1~an
$(ja1{)}^2+(ja2{)}^2+...+(jan{)}^2$ = $j^2\ast n+2\ast j\ast (a1+a2+...+an)+a{1}^2+a{2}^2+...+a{n}^2$
考虑状态$f[i][j][a][b]$
表示有i位，最高位为j，数的大小%7为a，数的位数和%7为b的所有解。
需要保留3个状态用于继承。
s0用于保存个数。
s1用于保存一次方和。
s2用于保存二次方和。
用这三个状态可以预处理，还有取模方面的问题。（少生孩子多取模），其他细节问题见代码。

#include 
using namespace std;
const int N = 20;
const int P = 1e9 + 7;
typedef long long LL;
struct F{
	LL s0;
	LL s1;
	LL s2;
} f[N][10][7][7];
LL power7[N],power9[N];
LL Mod(LL l,int r){
	return (l % r + r) % r;
}
void init(){
	for(int i = 0;i <= 9;i ++){
		if(i == 7) continue;
		f[1][i][i % 7][i % 7].s0 ++;
		f[1][i][i % 7][i % 7].s1 += i;
		f[1][i][i % 7][i % 7].s2 += i * i;
	}
	LL power = 10;
	for(int i = 2;i < N;i ++,power *= 10){
		for(int j = 0;j <= 9;j ++){
			if(j == 7) continue;
			for(int a = 0;a < 7;a ++)
				for(int b = 0;b < 7;b ++){
					for(int k = 0;k <= 9;k ++){
						if(k == 7) continue;
						F v = f[i - 1][k][Mod(a - power  * j,7)][Mod(b - j,7)];
						f[i][j][a][b].s0 = Mod(f[i][j][a][b].s0 + v.s0,P);
						f[i][j][a][b].s1 = Mod(((f[i][j][a][b].s1 + v.s1) % P + j * (power % P) % P * v.s0 % P),P);
						f[i][j][a][b].s2 = Mod((f[i][j][a][b].s2 + 
											j * j % P * (power % P) % P * (power % P) % P * v.s0 % P + 
											2 * j % P * (power % P) % P * v.s1 % P + v.s2),P);
					}
				}
		}
	}
	power7[0] = power9[0] = 1;
	for(int i = 1;i < N;i ++){
		power7[i] = (power7[i - 1] * 10) % 7;
		power9[i] = (power9[i - 1] * 10ll) % P;
	}
	return;
}
F get(int i,int j,int a,int b){
	LL s0 = 0,s1 = 0,s2 = 0;
	for(int x = 0;x < 7;x ++)
		for(int y = 0;y < 7;y ++){
			if(x != a && y != b){
				auto v = f[i][j][x][y];
				s0 = (s0 + v.s0) % P;
				s1 = (s1 + v.s1) % P;
				s2 = (s2 + v.s2) % P;
			}
		}
	return {s0,s1,s2};
}
LL dp(LL x){
	if(! x) return 0;
	vector <int> v;
	LL return_n = x % P;
	while(x){
		v.push_back(x % 10);
		x = x / 10;
	}
	LL last_a = 0,last_b = 0;
	LL res = 0;
	for(int i = v.size() - 1;i >= 0;i --){
		for(int j = 0;j < v[i];j ++){
			LL a = Mod(-last_a * power7[i + 1],7);
			LL b = Mod(-last_b,7);
			auto v = get(i + 1,j,a,b);
			res = Mod(res + 
			(last_a % P) * (last_a % P) % P * power9[i + 1] % P * power9[i + 1] % P * v.s0 % P + 
			2 * (last_a % P) % P * power9[i + 1] % P * v.s1 % P +
			v.s2,P
			);
		}
		if(v[i] == 7) break;
		last_a = last_a * 10 + v[i];
		last_b = Mod(last_b + v[i],P);
		if(! i && last_a % 7 && last_b % 7 ) res = Mod(res + return_n % P * return_n % P,P);
	}
	return res;
}
int main(){
	init();
	int t;
	cin >> t;
	while(t --){
		LL l,r;
		cin >> l >> r;
		cout << (dp(r) - dp(l - 1) + P) % P << endl;
	}
	return 0;
}