MATLAB
一、基础
1.数据类型
整型、单精度浮点型、双精度浮点型、逻辑型、字符串型、单元数组、结构体类型和函数句柄
| 数据类型 | 说明 |
| int8,int16,int32,int64 | 有符号整型 |
| unit8,unit16,unit32,unit64 | 无符号整型 |
| single | 单精度浮点型 |
| double | 双精度浮点型 |
| logical(就是bool) logical(z):将z转换为相反的布尔型(0→1,1→0) |
逻辑型 |
| char | 字符串型 |
| cell | 单元数组型 |
| struct | 结构体型 |
| function_handle | 函数句柄型 |
1.1取整函数
| 函数 | 说明 |
| round | 向最接近的整数取整,四舍五入 |
| fix | 向0取整 |
| floor | 小数位只舍不入 |
| ceil | 小数位只入不舍 |
1.2复数
| 函数 | 说明 |
| complex() | 创建复数,a为实部,b为虚部 |
| real(z) |
得到复数z的实部 |
| imag(z) | 得到复数z的虚部 |
| abs(z) | 得到复数z的模 |
| angle(z) | 得到复数z的角度 |
| conj(z) | 得到复数z的共轭复数 |
1.3数据显示格式
只改变数据的显示格式,不改变数据的值
直到下一次使用format,否则显示方式不变
| format函数格式 | 说明 |
| format short或format('short') | 恢复默认显示,保留小数点后四位 |
| format long或format('long') | 有效数字16位 |
| format long e | 有效数字16位加3位指数 |
| format short e | 有效数字5位加3位指数 |
| format bank或format('bank') | 保留两位小数位 |
| format +或format('+') | 只给出正、负 |
| format rational或format('rational') | 以分数形式表示 |
| format hex或format('hex') | 16进制数 |
| format long g | 15位有效数 |
| format short g | 5位有效数 |
1.4结构体类型
| 格式 | 说明 |
| struct() | 产生结构体变量 |
| rmfield() | 删除结构体中的成员变量 |
| isstruct() | 判断是否为结构体变量 |
| isfield() | 判断是否为结构体变量的成员变量 |
| fieldnames() | 获得结构体的成员变量名字 |
| orderfields(S) | 按照成员变量的字母顺序排序 |
| getfield() | 取得存储在结构体中的成员变量的值; |
| setfield() | 用于给结构体的成员变量设置新值; |
| struct2cell) | 将结构体变量转换为单元数组 |
二、数组
1.表示
clear all;
A=[];%空向量
B=[1 2 3 4 5];
C=[1,2,3,4,5];
D=[1;2;3;4;5];
b1=B(3);%第三个元素
b2=B(2:4);%2-4个元素
b3=B(3:end);%3-最后一个元素
b4=B(3:-1:1);%3开始倒序输出
b5=B(end:-1:1);%数组元素的倒序输出
b6=B([2 4]);%第二位和第四位2.乘除法
1/0 = +∞(Inf)
A1=[1 2 3 4 5];
B1=[0 1 3 5 2];
%数组乘法
C1=A1.*B1;%A和B中对应元素相乘
D=A1*3;%A中每个元素*3
%数组除法
C2=A1./B;%A/B对应相除
D2=A1./3;%A每个元素除3
E2=A1.\B;%B/A对应相除3.比较运算符
%比较
A3=[11 10 13 4 5];
B3=[3 15 21 6 5];
C3=A3<=10; % 0 1 0 1 1
D3=A3>10; % 1 0 1 0 0
E3=A3>B3; % 1 0 0 0 0
F3=A3==B3; % 0 0 0 0 1
A(A>10)=10;%A大于10的赋值为10
B(B==5)=100;%B等于5的元素赋值为100
C4=A3&B3; % 1 1 1 1 1
D4=A3|B3; % 1 1 1 1 1
E4=~A3; % 0 0 0 0 0
4.数组大小
size()获取数组的行数和列数,length()获取一维数组的长度
(若为二维数组,返回行数和列数的较大者
ndims()返回数组维数,总是>=2
%大小
A4=[11 0 0 1 5];
b4=size(A4); % [1,5]
[m,n]=size(A4); % m=1,n=5
length(A4); % 5
n1=ndims(A4); % 2三、矩阵
矩阵的元素按照列进行存储
%矩阵
A5=[1:4;5:8];
% 1 2 3 4
% 5 6 7 8
f1=A5(2,3); % 7
f2=A5(2); % 5
f3=A5(4); % 6
A6=[1:4;5:8;9:12;13:16];
f61=A6(1,:); % [1,2,3,4]
f62=A6(:,3); % [3;7;11;15] 第三列
f63=A6(1:2,1:2); % [1,2;5,6]
f64=A6(1:end,end); % [4;8;12;16]
1.矩阵的扩展
2.转置
转置操作符(’)
- 若矩阵中含有复数,矩阵转置后,复数转化为共轭复数
转置语言A.'(或transpose(A))
- 即使为复数,也不转换为共轭
3.伴随矩阵、逆矩阵
伴随矩阵:compan(u)
逆矩阵:inv()
4.旋转
可以采用转置的方式,也可以采用rot90()
| 函数 | 说明 |
| rot90(A) | 将矩阵逆时针旋转90度 |
| rot90(A,k) | 将矩阵逆时针旋转90度的k倍,k默认为1 |
5.翻转
左右翻转是将原矩阵的第一列和最后一列调换、第二列与倒数第二列调换...
- fliplr(A)
上下翻转是将原矩阵的第一行和最后一行调换、第二行与倒数第二行调换...
- flipud(A)
6.矩阵尺寸
Y=reshape(X,m,n)
将矩阵转化为m行n列的二维矩阵。矩阵总元素数不变。
矩阵是按列计数的
7.矩阵乘法
A*B,要求A的列数等于B的行数。
矩阵AB的点乘为A.*B,表示矩阵A和B中对应元素相乘,要求A B有相同维数。
8.差分
| 函数 | 说明 |
| Y=diff(X) | 计算矩阵各列的差分 |
| Y=diff(X,N) | 计算矩阵各列的N阶差分 |
| Y=diff(X,N,DIM) | 计算矩阵在反向DIM上的N阶差分 DIM=1时,计算各列元素的差分 DIM=2时,计算各行元素的差分 |
9.特殊矩阵
| 函数 | 说明 |
| zero() | 全0矩阵 |
| one() | 全1矩阵 |
| eye() | 生成单位矩阵(对角线元素是1) |
10.方阵的行列式
clear all;
A=magic(3);
B=[1:3;2 5 7;3 8 7];
y1=det(A); %-360
y2=det(B); %-411.矩阵的特征向量和特征值
| 函数 | 说明 |
| E=eig(A) | A的全部特征值,组成向量E |
| [V,D]=eig(A) | 方阵V的每列为一个特征向量 方阵D为对角矩阵,对角线上的元素为特征值 |
A=magic(3);
E=eig(A);
[V,D]=eig(A);
四、多项式
1.多项式的建立
根据系数建立
clear all;
%根据系数建立多项式
p1=[4 3 2 1];
y=poly2sym(p1); %创建多项式
disp(y); %显示多项式
% y=4*x^3 + 3*x^2 + 2*x + 1
根据多项式的跟显示多项式
%根据多项式的跟显示多项式
r=[2 3 4];
p=poly(r);
y=poly2sym(p); %多项式p的系数向量
disp(y); % 显示多项式
% x^3 - 9*x^2 + 26*x - 242.多项式的求值与求根
| 函数 | 说明 |
| polyval() | 以数组或矩阵中的元素为计算单位 |
| polyvalm() | 以矩阵为计算单位 |
3.多项式的导数和积分
| 求导函数 | 说明 |
| y=polyder(p) | 对以向量p为系数的多项式求导 |
| y=polyder(a,b) | 对以a和b为系数的多项式的乘积求导 |
| [q,d]=polyder(b,a) | 以b为系数的多项式除以以a为系数的多项式的商的导数,以q/d的格式表示 |
| 积分函数 | 说明 |
| polyint(p) | 返回以向量p为系数的多项式积分,积分的常数项为默认项 |
| polyint(p,k) | 返回以向量p为系数的多项式的积分,积分常数项为k |
4.多项式展开
clear all;
b=[1 -1 -7 -1];%分子多项式->系数
a=poly([1;5;6]);%分母多项式->根
[r,p,k]=residue(b,a);%多项式展开
[b1,a1]=residue(r,p,k);%通过余数、极点和常数项来求分子分母
b1=poly2sym(b1)
a1=poly2sym(a1)
b=[1 -1 -7 -1];
a=poly([1;1;1]);%有三重根
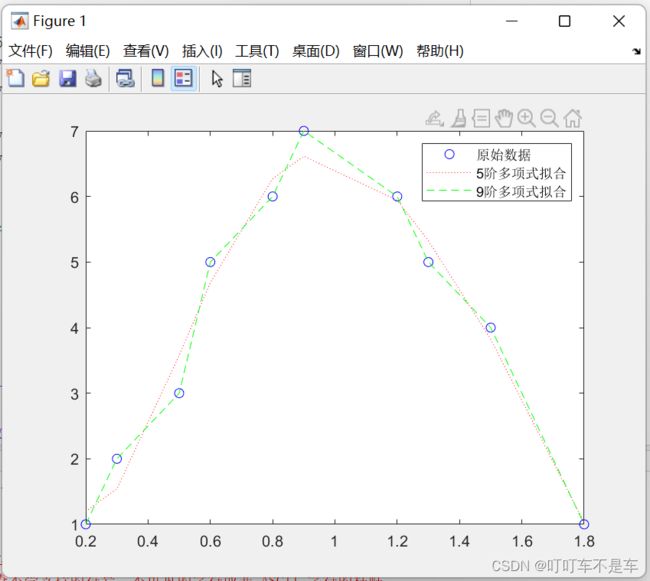
[r,p,k]=residue(b,a);5.多项式拟合
p=polyfit(x,y,n);采用最小二乘法对给定的数据进行多项式拟合,采用n次多项式来拟合数据x和y,得到以p为系数的多项式。
clear all;
x=[0.2 0.3 0.5 0.6 0.8 0.9 1.2 1.3 1.5 1.8];
y=[1 2 3 5 6 7 6 5 4 1];
p5=polyfit(x,y,5);%5阶多项式拟合
y5=polyval(p5,x);
p5=vpa(poly2sym(p5),5);%显示5阶多项式,精度为5
p9=polyfit(x,y,9);%9阶多项式拟合
y9=polyval(p9,x);
figure;%画图显示
plot(x,y,'bo');
hold on;
plot(x,y5,'r:');%二维线画图函数
plot(x,y9,'g--');
legend('原始数据','5阶多项式拟合','9阶多项式拟合');6.曲线拟合图形用户接口
五、插值
1.一维插值
- 基于多项式的插值
- interpre1()
- 基于快速傅里叶的插值
- interpft()
2.二维插值
主要用于图像处理和数据的可视化
| 函数 | 说明 |
| zi=interp2(x,y,z,xi,yi) | 通过初始数据x,y和z产生插值函数y=f(x,y),返回值zi是(xi,yi)在函数f(x,y)上的值 |
| zi=interp2(x,y,z,xi,yi,method) | 其中method为可采用的插值方法 ‘nearest’,‘linear’(默认),‘spline’,‘cubic‘ |
3.样条插值
| 函数 | 说明 |
| yi=spline(x,y,xi) /yi=spline(x,y,xi,'spline') |
通过初始数据产生插值函数,然后对数据xi进行插值,返回值yi=f(xi) |
| pp=spline(x,y) yi=ppval(pp,xi) |
通过对初始数据x和y产生插值函数(pp),并返回。利用ppval()对数据xi进行插值计算 |
4.高维插值
interpn(),代表进行n维插值,与二位插值具体内容一致
六、积分微分
1.定积分
- 采用trapz()可以直接采用梯形法解定积分的近似值。
- 矩形求面积
函数 说明 y=cumsum(X) 采用矩形法计算定积分的近似值 y=cumsum(X,DIM) 在第DIM维计算定积分的近似值
clear all; #梯形法 X1=[1 2 3 4 5 6 7]; z1=trapz(X1); X2=[1 2 3;3 6 8;2 5 9]; z2=trapz(X2); z3=trapz(X2,2); x=[1 2 3]; z4=trapz(x,X2);
单变量数值积分求解
采用函数quad()求解定积分的数值解(quadl()方式格式与quad()一致,精度速度高于quad())
函数 说明 y=quad(Fun,a,b) 函数Fun的定积分,下限为a上限为b y=quad(Fun,a,b, )
输入参数 来指定误差限,默认为
syms x; f=inline('1./(sin(x)+exp(-x.^2))'); y=quad(f,0,1.3); y1=quad(@myfun1,0,1.3); y2=quad(@myfun1,0,1.3,1.e-10); function y=myfun1(x) y=1./(sin(x)+exp(-x.^2)); end脚本中的函数定义必须出现在文件的结尾。
2.双重积分求解
采用函数dblquad()计算双重积分的数值解
函数 说明 q=dblquad(Fun,xm,xM,ym,yM) 函数计算矩形区域的双重积分 q=dblquad(Fun,xm,xM,ym,yM, )
函数限定双重积分的精度为 syms x; f=inline('x*cos(y)+y*sin(x)','x','y'); y=dblquad(f,pi,2*pi,0,pi); y2=dblquad(@(x,y) x*cos(y)+y*sin(x),pi,2*pi,0,pi);
3.三重积分求解
采用函数trlplequad()计算三重积分的数值解
函数 说明 q=trlplequad(Fun,xm,xM,ym,yM,zm,zM) 函数计算矩形区域的双重积分 q=trlplequad(Fun,xm,xM,ym,yM,zm,zM )
函数限定双重积分的精度为 syms x; f=inline('z*cos(x)+y*sin(x)','x','y','z'); q=triplequad(f,0,pi,0,1,-1,1); q1=triplequad(@(x,y,z) z*cos(x)+y*sin(x),0,pi,0,1,-1,1); q2=triplequad(@(x,y,z) z*cos(x)+y*sin(x),0,pi,0,1,-1,1,1.e-10); q3=triplequad(@(x,y,z) z*cos(x)+y*sin(x),0,pi,0,1,-1,1,1.e-10,@quad);
4.常微分方程
符号解
采用函数dsolve()求解(Dy表示一阶微分项,D2y表示二阶微分项)
函数 说明 dsolve('equation') 函数求微分方程的通解 dsolve('equation','condition') 函数求微分方程的特解 dsolve('equation','condition',...,'condation1','condition2') 函数求微分方程组 dsolve(...,'v') 函数求微分方程,并表示为v的函数
数值解
提供7种解法:ode45()、ode23()、ode113()、ode15s()、ode23s()、ode23t()、ode23tb()
5.函数的极小值和零点
采用fminbnd()求解一元函数在给定区间内的最小值
函数 说明 X=fminbnd(fun,x1,x2) 函数在区间[x1,x2]内寻找函数fun的最小值 X=fminbnd(fun,x1,x2,options) 函数采用option进行优化器的设置 [x,fval]=fminbnd(...) 函数返回输出变量最小值fval
6.一元函数的零点
采用fzero()寻找零点
七、概率和数理统计
1. 二项分布随机数据的产生
采用函数binornd()
函数 说明 R=binornd(N,P) 函数中N和P为二项分布的两个参数,返回服从参数为N和P的二项分布随机数 R=binornd(N,P,M) 函数中参数M指定随机数的个数
2.泊松分布
采用函数poissrnd()
函数 说明 R=possirnd(LAMBDA) LAMBDA为泊松分布的参数,返回服从参数为LAMBDA的泊松分布随机数,其中R和LAMBDA维数相同 R=poissrnd(LAMBDA,M,N) 在该函数中LAMBDA为泊松分布随机数矩阵,矩阵大小为M*N
3.指数分布
采用exprnd()生成具有指数分布的随机数据
函数 说明 R=exprnd(MU) 函数返回一个以MU为参数的指数分布的随机数,其中R和MU同维度 R=exprnd(MU,M,N) 函数返回一个以MU为参数的指数分布的随机数矩阵,该矩阵大小为M*N
4.均匀分布随机数据
连续型均匀分布
采用unifrnd()产生数据
函数 说明 R=unifrnd(A,B) 函数返回区间[A,B]上的连续型均匀分布 R=unifrnd(A,B,M,N) 函数返回区间[A,B]上的连续型均匀分布矩阵
离散型均匀分布
采用unidrnd()产生数据
函数 说明 R=unidrnd(N) 函数返回一个离散型均匀分布,R和N 同维数 R=unidrnd(N,MM,NN) 函数返回一个离散型均匀分布矩阵,矩阵大小为MM*NN
5.正太分布随机数据
采用函数normrnd()
八、二维数据可视化
采用函数plot()
1.子图绘制
- 采用函数subplot()进行子图绘制。可以将几个图形在同一个图形窗口绘制出来,并采用不同的坐标系。
- subplot(m,n,p):函数将当前图形窗口分成m*n个绘图区,即共m行,每行n个,子绘图区的编号按行优先从左到右编号。该函数选定第p个子图为当前活动区,每个子图绘区允许以不同的坐标系单独绘制图形。
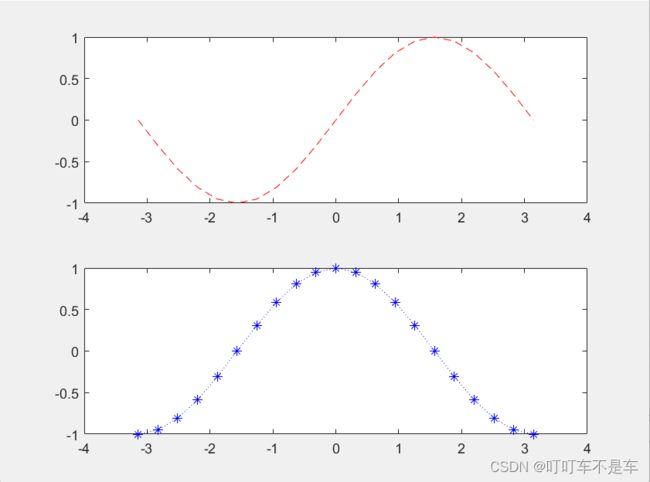
clear all;
x=-pi:pi/10:pi;
figure;
subplot(2,1,1);%分成两行一列,第一个子图绘制sin(x)
plot(x,sin(x),'r--');
subplot(212);%第二个子图绘制cos(x)
plot(x,cos(x),'b:*');x=-pi:pi/10:pi;
figure;
subplot(2,2,1);
plot(x,sin(x),'r--');
subplot(223);
plot(x,cos(x),'b:*');
subplot(2,2,[2 4]);
plot(x,sin(x)+cos(x),'b-.^')2.叠加图绘制
| 函数 | 说明 |
| hold on | 启动图形保持功能,允许在同一坐标轴上绘制多个图 |
| hold off | 关闭图形保持功能,不能在当前坐标轴上在绘制图形 |
| hold | 在两种状态hold on和hold off之间进行切换 |
| hold all | 实现hold on功能,并且使新的绘图函数依然按顺序循环使用当前坐标系中的ColorOrder和LineStyleOrder两个属性 |
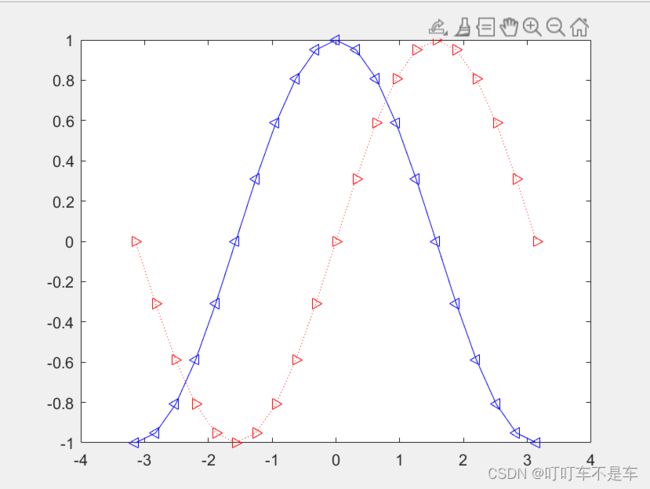
x=-pi:pi/10:pi;
figure;
plot(x,sin(x),'r:>');
hold on;
plot(x,cos(x),'b-<');3.设置坐标轴
| 函数 | 说明 |
| axis([xmin xmax ymin ymax]) | 函数用于定义x轴和y轴的范围 |
| axis([xmin xmax ymin ymax zmin zmax]) | 函数用于定义,x,y,z轴的范围 |
| axis([xmin xmax ymin ymax zmin zmax cmin cmax]) | 函数用于定义,三维坐标轴的范围,以及图形颜色信息 |
4.获取和标记数据点
| 函数 | 说明 |
| [x,y]=ginput(n) | 函数通过鼠标选择n个点,坐标值保存在变量和中,可以通过enter键结束 |
| [x,y]=ginput | 函数通过鼠标选择多个点,坐标值保存在和中,通过enter键结束 |
| [x,y,button]=ginput(...) | 函数返回值记录了在用鼠标选点时的相关信息 |
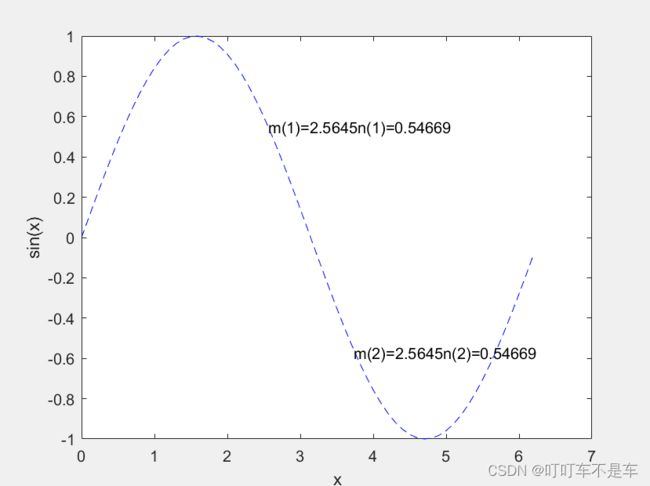
x=0:0.1:2*pi;
y=sin(x);
figure;
plot(x,y,'--b');
xlabel('x');
ylabel('sin(x)');
[m,n]=ginput(2);
text(m(1),n(1),['m(1)=',num2str(m(1)),'n(1)=',num2str(n(1))]);
text(m(2),n(2),['m(2)=',num2str(m(1)),'n(2)=',num2str(n(1))]);