LIO论文阅读：Tightly Coupled 3D Lidar Inertial Odometry and Mapping

论文地址与代码地址

论文：arxiv
代码：GitHub

摘要

Ego-motion 在移动机器人应用中很重要。传感器融合可以补偿单传感器缺陷。这篇文章主要介绍了一种LiDAR-IMU 融合的方法，通过联合优化IMU和LiDAR的测量数据，可以做到在LiDAR退化的情况下也没有明显漂移。
另外，本文提出了一种rotation-constrained refinement 算法（LIO-mapping），用于配准LiDAR位姿和全局地图。
实验结果显示，所提出的方法可以做到以IMU的速率估计传感器的位置，即使在快速移动和缺少特征情况下也能工作。

I. INTRODUCTION

LiDAR优点：在机器人领域广泛应用，频率10Hz，水平的 field of view(FOV)是360 $°$。受光照影响小，高精度和高可靠性。

LiDAR的缺点：竖直方向上分辨率太小，太过于稀疏，因此能提供的特征也很少，让特征跟踪变得棘手。
安装在机器人上的LiDAR由于机器人的运动，会使测量的数据变差。
另外，在一个狭窄的走廊环境中，只能得到部分天花板，墙和底板的点云。特征过少导致跟踪的丢失。
还有一个问题：更新频率太低。

在本文中，提出IMU-LiDAR紧耦合的位姿估计算法来解决上述问题。
使用了 fix-lag smoothing 和 原有位姿边缘化的方法达到实时和一致性的估计，然后再进行 rotation-constrained refinement。

主要工作如下：

• LiDAR-IMU紧耦合算法提供高频的，实时的，准确的位姿估计。
• rotational constrained refinement 方法优化最终的位姿并且产生点云地图，提高一致性和鲁棒性的估计。
• 算法在室内外环境都进行了测试，效果比松耦合算法优异。
• 算法开源，业界第一个LiDAR-IMU紧耦合算法。

本文总体结构：
II 介绍相关工作；
III 介绍标记与注记；
IV 介绍里程计算法；
V 介绍 refinement （配准）算法；
VI 和 VII 介绍了实现与测试结果；
VIII 结论。

II. RELATED WORKS

松耦合算法：将LiDAR和IMU的状态估计分别单独考虑。
[1] 中的雷达里程计算法带有IMU的辅助信息。使用加速度信息时会假设它是 zero velocity 的。它将 IMU 和雷达的数据分离，并且将IMU信息作为整个系统的先验，因此在优化中，它没有最大化 IMU 信息的利用。
[2] 中使用EKF来融合2D 情况下的 LiDAR 和 IMU 的信息，但它不能处理3D或者更复杂的环境。
[3] 讲了一种模块化的IMU融合方式，通过 EKF 进行融合。这种松耦合的方式虽然计算效率很高，但是和紧耦合的相比准确度不够，因为它只把里程计作为一个黑盒，却没有通过IMU来更新它。
[4]采用了紧耦合的方式。
[5] 是 Soloviev 等人提出的。针对2D平面运动估计，他们提出了一种方法：抽取和匹配2D平面的线特征。通过 IMU 的预测方位补偿雷达信息。过程中应用了 卡尔曼滤波器。
[6] Hemann 等人提出了以误差状态的卡尔曼滤波器形式，紧耦合IMU 传播误差和 LiDAR heightmap。这种方式在环境地图已知时，没有GPS信息也能长时间工作，但没有地图无法工作。
[7] 和 [8] 未处理数据和 IMU 的预测数据直接用于计算残差和进行优化。这种方式没有牵涉转化和状态估计，在系统快速运动时，系统会不可用。

受到其他 VI 方式启发，如[10] ,[11] ，我们基于预积分和紧耦合的方式设计了整个系统。使用未处理的IMU数据和LiDAR数据进行状态优化。
整个系统可以在雷达退化或者运动十分快速时也能工作得很好。
据我们所知，我们的系统是少数几个适合复杂3D环境的。

III. NOTATIONS AND PRELIMINARIES

A. Notations

雷达每一线的测量记为 $scanC$。
包含所有 $scan$ 的一次测量记为 $sweepS$。16线雷达在一次sweep中包含16个scan。

变换矩阵${\mathbf{T}}_b^a\in SE(3)$,表示把点 ${\mathbf{x}}^{\mathbf{b}}\in {\mathbb{R}}^3$ 从坐标系 $F_b$ 变换到坐标系 $F_a$；
${\bar{\mathbf{T}}}_b^a$表示IMU预测的变换；
${\mathbf{R}}_b^a\in SO(3)$ 和 ${\mathbf{p}}_b^a$ 分别是${\mathbf{T}}_b^a$的旋转和平移部分；
四元素${\mathbf{q}}_b^a$对应于${\mathbf{R}}_b^a$；

${\hat{\mathbf{a}}}_k$和${\hat{\omega }}_k$表示在时刻 $k$ 时，IMU的加速度和角速度测量；

在坐标系 $F_a$下抽取的特征表示为 ${\mathbf{F}}_a$， ${\mathbf{F}}_a$可以通过 ${\mathbf{F}}_a^b$变换到坐标系 $F_b$。

A. IMU Dynamics

1）状态
$F_{B_i}$ 和 $F_{L_i}$ 分别是IMU和雷达的坐标系；
雷达在离散时刻 $i$ 时接收 $sweep{S}_i$；

我们要进行估计的是IMU在世界坐标系下 $F^W$ 的状态 ${\mathbf{X}}_{B_i}^W$以及雷达和IMU之间的外参 ${\mathbf{T}}_B^L$，具体如下：
$$\begin{gathered} {\mathbf{X}}_{B_i}^W=[{{\mathbf{p}}_{B_i}^W}^T{{\mathbf{v}}_{B_i}^W}^T{{\mathbf{q}}_{a_i}^W}^T{{\mathbf{b}}_{g_i}^W}^T{]}^T, \\ {\mathbf{T}}_B^L=[{{\mathbf{p}}_B^L}^T{{\mathbf{q}}_B^L}^T]\text{\hspace{1em}(1)} \end{gathered}$$
上面的公式中：
${\mathbf{p}}_{B_i}^W$ 是当前body frame相对于世界坐标系的位置；
${\mathbf{v}}_{B_i}^W$ 是当前body frame相对于世界坐标系的速度；
${\mathbf{q}}_{B_i}^W$ 是当前body frame相对于世界坐标系的姿态；
${\mathbf{b}}_a$是IMU的加速度偏置；
${\mathbf{b}}_g$是IMU的角速度偏置；

2）动态模型
输入：IMU的加速度和角速度；
输出：${\mathbf{X}}_{B_k}^W$，将${\mathbf{X}}_{B_i}^W$ 更新到${\mathbf{X}}_{B_j}^W$ ；
更新方程如下：

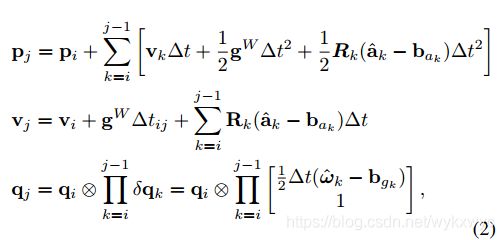
方程内：
$\Delta t$是两次IMU连续测量的时间间隔；
我们积分的时间区间是两次雷达扫描之间的时间；
${\mathbf{g}}^W$是世界坐标系下的重力；

简写：
$(\cdot {)}_i\dot{=}(\cdot {)}_{B_i}^W$,
$\Delta t_{ij}={\Sigma }_{k=i}^{j-1}\Delta t$ ,
${\prod }_{k=i}^{j-i}$是四元素的连乘；

3）预积分
在时刻 $i$ 到时刻 $j$ 之间，body frame 的运动可以通过预积分得到：
$$z_j^i=\{\Delta {\mathbf{p}}_{ij},\Delta {\mathbf{v}}_{ij},\Delta {\mathbf{q}}_{ij}\}$$
$z_j^i$具有协方差${\mathbf{C}}_{B_j}^{B_i}$
这部分参考补充材料。

IV. TIGHTLY COUPLED LIDAR-IMU ODOMETRY

受到[7],[1],[3]的启发，他们将里程计和建图两部分分开。
本文也分成两个部分：
Sec. IV介绍紧耦合的lidar-IMU里程计，在局部窗口中优化所有的状态；
Sec. V介绍rotation constrained refinement 过程，这是一个全局建图过程。

A. Lidar-IMU Odometry Overview
lidar-IMU里程计系统整体框图：

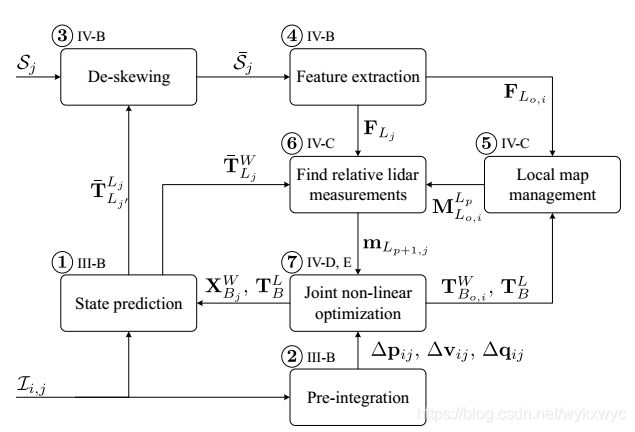
输入是 lidar raw inputs $S_j$ 和 IMU raw inputs $I_{i,j}$
步骤：
1）在 $S_j$ 接收到之前，IMU状态通过公式-2进行迭代;
2）同时预积分得到 $\Delta {\mathbf{p}}_{ij},\Delta {\mathbf{v}}_{ij},\Delta {\mathbf{q}}_{ij}$；
3）接收到 $S_j$ 后，进行校正，然后得到 ${\bar{S}}_j$;
4）进行特征抽取，给数据降维，得到最重要的特征点 ${\mathbf{F}}_{L_j}$;
5）上一次雷达特征点 ${\mathbf{F}}_{L_{o,i}}$ 根据上一次的对应优化状态 ${\mathbf{T}}_{b_{o,i}}^W$ 和 ${\mathbf{T}}_B^L$，得到一个 local map ${\mathbf{M}}_{L_o,i}^{L_p}$;
6）根据对 ${\mathbf{F}}_j$时的 lidar pose 的预测，得到 lidar 的性对测量 ${\mathbf{m}}_{L_{p+1,j}}$;
7）联合优化，根据雷达得到的两帧之间的相对变换和IMU的预积分进行最大后验估计，估计的结果再去更新1）中 IMU 状态，避免 drift。

B. De-skewing and Feature Extraction
这一部分对应上面总体框图的步骤3，步骤4。

3D雷达在运动时得到的数据会有失真，解决方法如下：
1.使用和LOAM中类似的方法，假设了雷达的匀速运动模型。
2.然后从IMU状态中预测出 ${\bar{\mathbf{T}}}_{L_{j^{\prime }}}^{L_j}$。
3.对于每个点 $\mathbf{x}(t)\in S_j\subset {\mathbb{R}}^3$,通过 ${\bar{\mathbf{T}}}_{L_{j^{\prime }}}^{L_j}$ 线性插补，进行位姿校正并转换坐标系到 ending pose of the sweep，得到 ${\bar{S}}_j$。
4.这一 sweep 中的时间戳 $t\in (t_{j^{\prime }},t_j]$,$t_{j^{\prime }}$ 是 sweep 的开始，$t_j$ 是 sweep 的结束。

使用与LOAM中相同的提取特征边和特征平面的方法提高计算效率。
${\mathbf{F}}_{L_j}\in {\bar{S}}_j$通过曲率进行选择，选择最平的和最陡的。

C. Relative Lidar Measurements
这一部分对应上面总体框图的步骤5，步骤6。

为了和IMU预积分相适应，对于 lidar 数据采用 sweep 之间的相对位姿运动。算法如下面框图所示：

因为单个 sweep 不够稠密，计算准确的特征对应很困难，所以需要先建立一个local map。

local map包含 $N_m$ 个离散的时刻：
$$\{o,...,p,...,i\}$$
如下图所示，

$o$ 是第一个lidar sweep；
$p$ 是 pivot lidar sweep；
$i$ 是最后一个 lidar sweep；

local map ${\mathbf{M}}_{L_o,i}^{L_p}$ 采用 ${\mathbf{F}}_{L_{\gamma }}^{L_p}$ ,$\gamma \in \{o,...,i\}$的数据，并建立在pivot坐标系上。
${\mathbf{F}}_{L_{\gamma }}^{L_p}$ 经过上一时刻优化得到的 lidar poses ${\mathbf{T}}_{L_{\gamma }}^{L_p}$ （这里简写了，准确来说是${\bar{\mathbf{T}}}_{L_{\gamma }}^{L_p}$ ）。

需要被预测的状态是： $\{p+1,...,i,j\}$，里面：
$p+1$是 pivot的下一个时间戳；
$j$ 是窗口中当前的 lidar sweep。

有了local map之后，可以找到 ${\mathbf{M}}_{L_o,i}^{L_p}$ 和原始 ${\mathbf{F}}_{L_{\alpha }}$ ,$\alpha \in \{p+1,...,j\}$ 之间的对应关系。
这种对应关系实质就是相对雷达运动，他们两者都是相对于他们的 pivot 位姿的运动，pivot 位姿会随着滑动窗口变化。

在 Sec. IV-B 中抽取的原始特征是坐标系 $F_{L\alpha }$ 中最平坦或者是 edge 点。
在实际中，edge对效果提高不明显，所以我们后面只针对平面点。

使用KNN找到 ${\mathbf{x}}^{L_p}\in {\mathbf{F}}_{L_{\alpha }}^{L_p}$ 的K个最近点 $\pi ({\mathbf{x}}^{L_p})\in {\mathbf{M}}_{L_o,i}^{L_p}$；
然后将这些点拟合到坐标系 $F_{L_p}$ 中的一个平面上去；
平面的系数通过如下方程确定：
$${\omega }^T{\mathbf{x}}^{\prime }+d=0,{\mathbf{x}}^{\prime }\in \pi ({\mathbf{x}}^{Lp})$$
$\omega$是平面的法向量；
$d$ 是距离坐标系 $F_{L_p}$ 原点 $o$ 的距离；

对于每个平面特征点 $\mathbf{x}\in {\mathbf{F}}_{L_{\alpha }}$,$m=[\mathbf{x},\omega ,d]\in {\mathbf{m}}_{L\alpha }$ 是它的相对雷达运动。
每个$m\in {\mathbf{m}}_{L_{\alpha }}$ , $\mathbf{x}$定义在坐标系 $F_{L_{\alpha }}$ 中，$d$ 定义在坐标系 $F_{L_p}$ 中。

D. Lidar Sweep Matching
这一部分对应上面总体框图的步骤7。

相对位姿提供的是pivot 和后续lidar poses之间的相对运动。
优化过程会优化窗口中的所有位姿，包括第一个位姿 ${\mathbf{T}}_{L_p}^W$（也就是说pivot所在的坐标系 $F_{L_p}$不是固定的）。
因此在lidar的 代价函数中，每个位姿都会涉及到两个量： ${\mathbf{T}}_{L_p}^W$ 和 ${\mathbf{T}}_{L_{\alpha }}^W,\alpha \in \{p+1,...,j\}$。
优化 pivot 的 pose 可以减小预积分误差。

估计的状态都是IMU的，因此需要通过IMU状态引入外参来表示 lidar constraints。
pivot 后面的 lidar poses 相对于 pivot 的相对位姿变换可以这样定义：

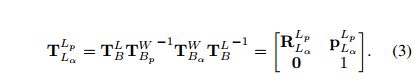
有了前面的对应关系，每个lidar 测量$m=[\mathbf{x},\omega ,d]\in {\mathbf{m}}_{L\alpha }$,$\alpha \in \{p+1,...,j\}$ 的残差都可以表示成点到平面的距离。

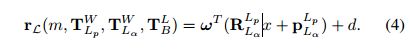
E. Optimization
这一部分对应总体框图的步骤7。

优化状态的获得通过 fixed-lag 平滑和边缘化。
fixed-lag 平滑在滑动窗口内保持 $N_s$ 个IMU 状态（${\mathbf{X}}_{B_p}^W$ 到 ${\mathbf{X}}_{B_j}^W$），图2所示。
当有新的测量数据进啦，平滑器将加入新的量，将窗口中最旧的量边缘化。
整个要估计的量是：
$$\mathbf{X}=[{\mathbf{X}}_{B_p}^W,...,{\mathbf{X}}_{B_j}^W,{\mathbf{T}}_B^L]\text{\hspace{1em}(5)}$$

然后去求下列马氏距离的代价函数的最小值，获的 $\mathbf{X}$ 的最大后验估计。

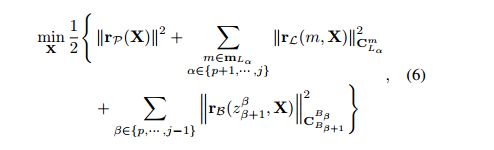
上面公式中：
${\mathbf{r}}_{\mathcal{P}}(\mathbf{X})$ 是边缘化的先验项；
${\mathbf{r}}_{\mathcal{L}}(m,\mathbf{X})$ 是 relative lidar constraints；
${\mathbf{r}}_{\mathcal{B}}(z_{\beta +1}^{\beta },\mathbf{X})$ 是 residual of the IMU constraints；
上面的非线性最小二乘的代价函数可以通过 Gauss-Newton 法按照 $\mathbf{H}\delta \mathbf{X}=-\mathbf{b}$ 的形式求解。LIO通过Ceres Solver 进行求解。

对于每个 lidar 的相对测量，可以从等式-4中获得 ${\mathbf{r}}_{\mathcal{L}}(m,\mathbf{X})$；
协方差矩阵 ${\mathbf{C}}_{L_{\alpha }}^m$ 由 lidar accuracy 决定；
IMU constraint ${\mathbf{r}}_{\mathcal{B}}(z_{\beta +1}^{\beta },\mathbf{X})$ 通过IMU的预积分获得，和[10]类似；
$||{\mathbf{r}}_{\mathcal{P}}(\mathbf{X})|{|}^2={\mathbf{b}}_{\mathcal{P}}^T{\mathbf{H}}_{\mathcal{P}}^{+}{\mathbf{b}}_{\mathcal{P}}$ 可以通过舒尔补获得[文献12]；

V. REFINEMENT WITH ROTATIONAL CONSTRAINTS

将特征点注册到全局地图坐标系 $F_W$ 而不是局部地图，能使lidar poses 具有一致性。refinement 方法使用相对lidar 测量 ${\mathbf{m}}_L$。
对齐最近的lidar 特征点到global map：

上面的公式中：
$\mathbf{T}={\mathbf{T}}_L^W$ 是小估计的lidar poses；
相对lidar 测量$m$ 中包含的 $\mathbf{x}$ 定义在坐标系 $F_L$ 中，系数 $\omega ,d$ 定义在 $F_W$ 中；
然后用一个相似的Gauss-Newton方法去优化 ${\mathbf{C}}_{\mathcal{M}}$;
优化方式：通过残差 ${\mathbf{C}}_{\mathcal{M}}$，${\mathbf{J}}_{\mathbf{p}}^{\mathbf{C}}$, ${\mathbf{J}}_{\theta }^{\mathbf{C}}$ , $\theta$ 是对应于四元素 $\mathbf{q}$ 的误差状态。

长时间的误差累积会使建图错误更大，LIO采取了和文献[16]类似的方法，以 SE(2)-constraints 优化SE(3)。
这种方法保证了最后的图总是和重力是对齐的。
图3说明了这种方法：

z轴方形的姿态有更高的不确定，而roll和pitch更准确，因此姿态的Jacobian对代价函数进行限制（详细的推导在文献[12]中）：

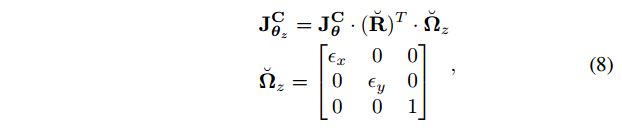
上面公式中：
$\breve{(\cdot )}$ 是上一次迭代的状态；
${\breve{\mathbf{\Omega }}}_z$ 是姿态相对于坐标系 $F_W$ 的信息矩阵的近似值；
${ϵ}_x$ , ${ϵ}_y$通过information ratio 获得；

然后，在优化步骤中通过${\mathbf{J}}_{\mathbf{p}}^{\mathbf{C}}$, ${\mathbf{J}}_{{\theta }_{\mathbf{z}}}^{\mathbf{C}}$作为Jacobians，lidar poses 的增量可以表示为 $\delta {\theta }_z$ 和$\delta \mathbf{p}$，然后获得状态的更新：

VI. IMPLEMENTATION

介绍关于以下四个方面的内容：

• 传感器配置
• 系统初始化
• 参数
• 室内及室外测试

A. Different Sensor Configurations
lidar和IMU距离很近的时候，算法按照上面介绍的进行就可以；
lidar和IMU距离远的时候，需要将外参加到 等式-6 (总体的最小二乘代价函数)，如下图：

B. Initialization
1.粗略的匹配算法使用LOAM的初始化方式；
2.当IMU和 lidar 的测量数据足够多的时候，可以用这些数据进行初始化；
3.在实验中，采用文献[10]的方式进行线性外参初始化；
4.最后再滑动窗口内进行非线性优化。

VII. TESTS AND ANALYSES

进行了室内和室外的实验，并提供定性和定量的分析。

A. Quantitative Analysis
1）不同环境下的测验：
LIO 是带有窗口优化的方法；
LIO-raw 是没有运动补偿的方法；
LIO-no-ex 是没有在线外参估计的方法；
LIO-mapping 是带有 rotaional constraints的方法，效果最好，速度在高速时效果更好，低速时漂移多一点。

2）随时间漂移
LIO-mapping 的效果比LOAM或LOAM+IMU的效果好。

B. Qualitative Results
进行了 KAIST Urban dataset 的实验，在视频中展示结果。

C. Running Time Analysis
配置：Intel i7-7700K CPU at 4.20GHz,16GB RAM
总结了室内室外雷达的建图运行时间。

VIII. CONCLUSION

1.提出了紧耦合的 lidar-IMU 融合方法；
2.LIO需要初始化，但是也更加鲁棒，更新频率也更高。