2D-2D：对极约束

上一篇博客记录了3D-2D：PnP算法，本篇博客记录一下2D-2D：对极约束算法，并简单谈一下自己理解。

1. 对极约束

首先我们要先搞清楚对极约束是用来干什么用的，然后在来搞清楚它的原理。

那么，对极约束是用来干什么用的呢？
答：在已知 2D 的像素坐标的前提下，根据两幅图像间多组2D像素点对来估计相机的运动。

搞清对极约束的用途之后，我们接着说它的原理。

1.1 物理意义

假设我们从两张图像中得到了一对配对好的特征点，那我们就来看看两个图像当中的匹配点有什么样的几何关系。

以上图为例，我们希望求取两帧图像之间的运动，设第一帧到第二帧的运动为R, t。两个相机中心分别为 O 1 , O 2 。现在,考虑第一幅图像中有一个特征点 p1 ,它在第二幅图像中对应着特征点 p2 。我们知道这对特征点是通过特征匹配得到的。如果匹配正确，说明它们确实是同一个空间点在两个成像平面上的投影。

这里我们需要一些术语来描述它们之间的几何关系。首先,连线 O1p1 和连线 O2p2 在三维空间中会相交于点 P 。这时候点O1 , O2 , P 三个点可以确定一个平面,称为极平面(Epipolar plane)。O1O2 连线与像平面 I1 , I2 的交点分为 e1 , e2 。e1 , e2 ,称为极点(Epipoles),O1O2 被称为基线(Baseline)。称极平面与两个像平面 I1 , I2 之间的相交线 L1 , L2 为极线(Epipolar line)。

直观上讲，从第一帧的角度上看，射线 O1p1 是某个像素可能出现的空间位置——因为该射线上的所有点都会投影到同一个像素点。同时，如果不知道 P 的位置，那么当我们在第二个图像上看时,连线 e2p2 (也就是第二个图像中的极线)就是 P 可能出现的投影的位置，也就是射线 O1p1 在第二个相机中的投影。现在，由于我们通过特征点匹配，确定了 p2 的像素位置，所以能够推断 P 的空间位置，以及相机的运动。

对极约束之所以称为约束，是因为我们在不知道P的真实空间位置的时候，通过几何关系将P点在第二帧图像上可能的投影位置约束在了一条直线上（即极线L2）。然后，通过特征匹配，我们确定p2与p1一样，都是空间点P的投影。

1.2 数学推导

接下来从数学角度描述一下对极约束。

在第一帧的坐标系下，设 P 的空间位置为:

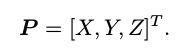
根据针孔相机模型,我们知道两个像素点 p 1 , p 2 的像素位置为:

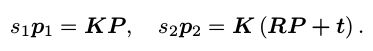
这里 K 为相机内参矩阵,R, t 为两个坐标系的相机运动(如果我们愿意,也可以写成李代数形式)。如果使用齐次坐标,我们也可以把上式写成在乘以非零常数下成立的(up to a scale)等式：

现在，取:

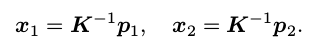
这里的 x1 , x2 是两个像素点的归一化平面上的坐标。代入上式，得:





这两个式子都称为对极约束，它以形式简洁著名。它的几何意义是 O1 , P, O2 三者共面。

注：以上数学推导过程摘自《视觉SLAM14讲》

对极约束的数学形式简单明了，我们可以看出，只要我们能够找出两幅图像之间的多组特征点关系，就可以根据对极约束求出两幅图像之间的运动关系。

我们把对极约束数学表达式中的中间部分记为两个矩阵：基础矩阵(Fun-damental Matrix)F 和本质矩阵(Essential Matrix)E，可以进一步简化对极约束:

对极约束简洁地给出了两个匹配点的空间位置关系。于是,相机位姿估计问题变为以下两步:

1. 根据配对点的像素位置，求出 E 或者 F ;
2. 根据 E 或者 F ，求出 R， t 。

本质矩阵和基础矩阵的求解在此不再赘述，可以参考《视觉SLAM14讲》的内容。

2 尺度不确定性

对于尺度不确定性，以前对它的理解总是不到位，经过查阅其他资料和自己的理解，我觉得现在我对它应该是理解透彻了。所以在此说一下。

《视觉SLAM14讲》对尺度不确定性的描述是这样的：

由于 E 本身具有尺度等价性，它分解得到的 t，R 也有一个尺度等价性。而 R ∈ SO(3) 自身具有约束，所以我们认为 t 具有一个尺度。换言之，在分解过程中，对 t 乘以任意非零常数，分解都是成立的。因此，我们通常把 t 进行归一化，让它的长度等于 1。

对 t 长度的归一化，直接导致了单目视觉的尺度不确定性(Scale Ambiguity)。例如，程序中输出的 t 第一维约 0.822。这个 0.822 究竟是指 0.822 米呢，还是 0.822 厘米呢，我们是没法确定的。因为对 t 乘以任意比例常数后，对极约束依然是成立的。换言之，在单目 SLAM 中，对轨迹和地图同时缩放任意倍数，我们得到的图像依然是一样的。这在第二讲中就已经给读者介绍过了。

**这段话是从数学的角度解释尺度不确定性。**其实，也可以从直观的看出单目视觉的尺度不确定性。

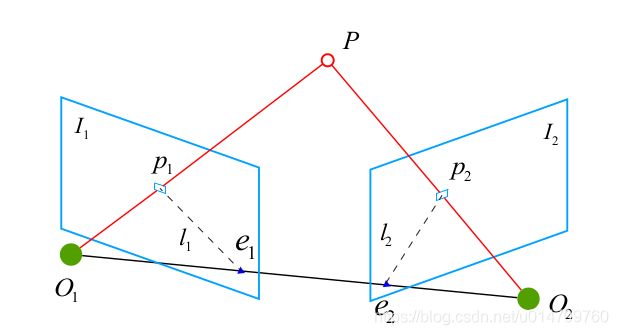
依旧看这幅图，根据对极约束原理和p1p2的坐标，我们可以求出两幅图像之间的运动关系（即R，t）。但是可以从图中看出，如果将第二帧图像和相机中心O2沿着直线O1O2左右移动，仍然满足对极约束。如下图所示

这就意味着，两个相机中心的距离O1O2是不确定的，也就是平移向量 t 的模值不确定，也就是尺度不确定。而尺度不确定的原因就在于P点空间位置不确定。

在单目视觉中，我们对两张图像的 t 归一化，相当于固定了尺度。虽然我们不知道它的实际长度为多少，但我们以这时的 t 为单位 1，计算相机运动和特征点的 3D 位置。这被称为单目 SLAM 的初始化。在初始化之后，就可以用 3D-2D 来计算相机运动了。初始化之后的轨迹和地图的单位，就是初始化时固定的尺度。因此，单目 SLAM 有一步不可避免的初始化。初始化的两张图像必须有一定程度的平移，而后的轨迹和地图都将以此步的平移为单位。

3 三角测量

3.1 什么是三角测量？

三角测量是指,通过在两处观察同一个点的夹角,确定该点的距离。

我们使用对极几何约束估计了相机运动在得到运动之后，下一步我们需要用相机的运动估计特征点的空间位置。这就是三角测量需要做的事情。

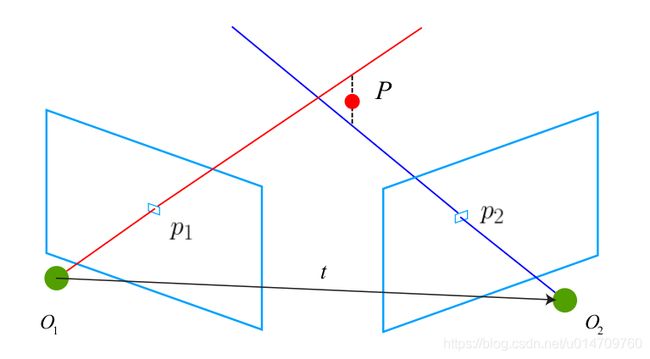
考虑图像 I1 和 I2 ，以左图为参考,右图的变换矩阵为 T 。相机光心为 O1 和 O2 。在 I1 中有特征点 p1 ，对应 I2 中有特征点 p2 。理论上直线 O1p1 与 O2p2 在场景中会相交于一点 P ，该点即是两个特征点所对应的地图点在三维场景中的位置。

其实，说的通俗一点，三角测量就是在已知两幅图像之间的变换关系和对应特征点的条件下构建一个三角形来确定两个特征点所对应的空间点的位置。当然，由于尺度不确定性，计算出的空间点位置和真实位置之间也存在尺度差异。

3.2 三角测量的数学表达

按照对极几何中的定义,设 x 1 , x 2 为两个特征点的归一化坐标,那么它们满足:

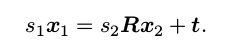
现在我们已经知道了 R, t,想要求解的是两个特征点的深度 s 1 , s 2 。当然这两个深度是可以分开求的,比方说先来看 s 2 。如果我要算 s2 ,那么先对上式两侧左乘一个 x^1 ,得:

该式左侧为零，右侧可看成 s 2 的一个方程，可以根据它直接求得 s 2 。有了 s 2 ,s 1 也非常容易求出。于是，我们就得到了两个帧下的点的深度，确定了它们的空间坐标。当然，由于噪声的存在，我们估得的 R, t,不一定精确使式(7.24)为零，所以更常见的做法求最小二乘解而不是零解。