机器人与matlab—Robotics Toolbox—01空间位姿描述
机器人学与matlab—Robotics Toolbox—01空间位姿描述
- 1、二维空间位姿描述
- 2、三维空间位姿描述
-
- 2.1 正交旋转矩阵
- 2.2 三角度表示法(欧拉角、RPY角)
- 2.3 等效轴角坐标系法
- 2.4 四元数表示法
1、二维空间位姿描述
(1)T=SE2(x,y,theta);
%代表(x,y)的平移和theta角度的旋转。
(2)trplot2(T);
%代表画出相对于世界坐标系的变换T。
(3)T=transl2(x,y);
%二维空间中,纯平移的齐次变换。
例子:
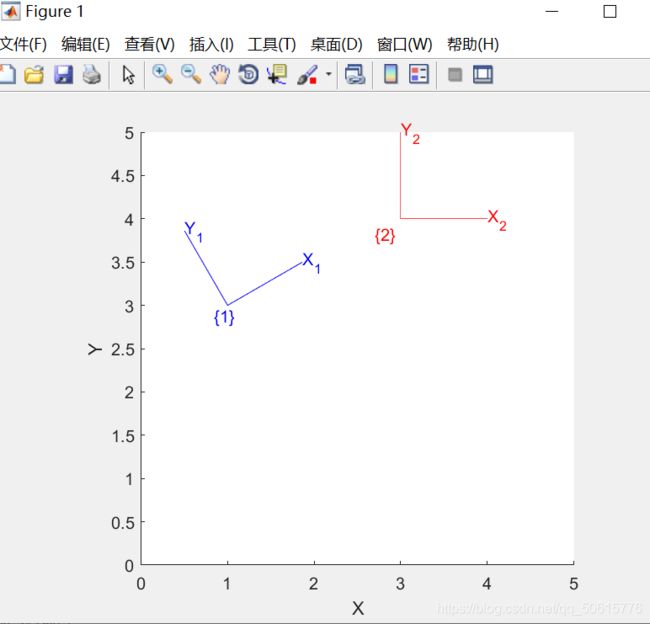
T1=SE2(1,3,30,'deg');%代表平移了(1,3)和旋转了30°,'deg'表示度数。
%%或者这样表示:T1=SE2(1,2,30*pi/180)
trplot2(T1,'frame','1','color','b');%代表画出相对于世界坐标系的变换T1,新的坐标系命名为坐标系1,并且颜色定义为'b',蓝色。
axis([0 5 0 5]);%设置世界坐标系坐标轴的范围:x轴为(0,5),y轴为(0,5)。
T2=transl2(3,4);%只做(3,4)平移的变换
%%或者这样表示:T2=SE2(3,4,0)
hold on;%让多图共存
trplot2(T2,'frame','2','color','r');%代表画出相对于世界坐标系的变换T2,新的坐标系命名为坐标系2,并且颜色定义为'r',红色。
2、三维空间位姿描述
2.1 正交旋转矩阵
(1)R=rotx(theta);
%绕x轴旋转theta角,得到的旋转矩阵。
(2)R=roty(theta);
%绕y轴旋转theta角,得到的旋转矩阵。
(3)R=rotz(theta);
%绕z轴旋转theta角,得到的旋转矩阵。
(4)trplot( R );
%绘制相应的旋转矩阵。
(5)tranimate( R );
%做一个旋转的动画。
(6)T=transl(x,y,z);
%坐标系到的平移。
(7)Tx=trotx(theta); Ty=troty(theta); Tz=trotz(theta);
%绕x、y、z轴旋转theta角,得到的齐次变换矩阵
例子:
R1=rotx(30,'deg')*roty(50,'deg');
trplot(R1,'frame','A','color','b');
tranimate(R1,'frame','A','color','b');
R2=roty(50,'deg')*rotx(30,'deg');
hold on;
trplot(R2,'frame','B','color','r');
tranimate(R2,'frame','B','color','r');
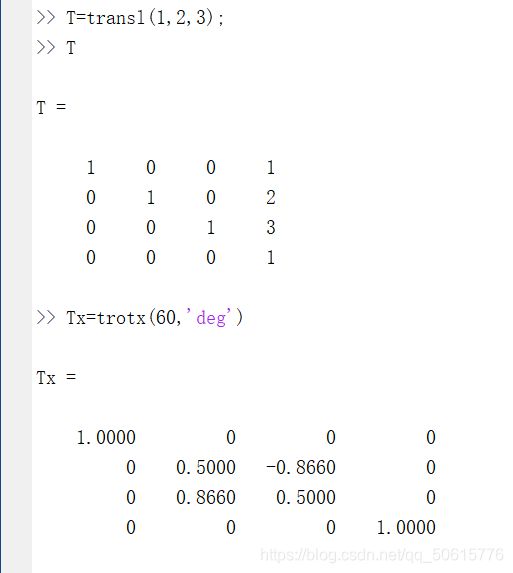
T=transl(1,2,3);
Tx=trotx(60,'deg');
2.2 三角度表示法(欧拉角、RPY角)
2.2.1 欧拉角
相对于运动坐标系,先绕Zb轴转,再绕Yb轴转,最后绕Xb轴转。
欧拉角:R=rotz(alpha ) * roty(beta) * rotz(gamma);
(1)eul=tr2eul( R );
%旋转矩阵用欧拉角表示。
(2)R=eul2r(eul);
%eul=[alpha beta gamma] . 欧拉角转换为旋转矩阵。
例子:
R3=rotz(0.1)*roty(0.2)*rotz(0.3);
eul=tr2eul(R3);%将旋转矩阵R3,转变为欧拉角。
R4=eul2r(0.1,0.2,0.3);%将欧拉角转变为旋转矩阵。
2.2.2 RPY角
相对于固定坐标系,先绕Xa轴,Ya轴再绕Za轴旋转。
RPPY角:R=rotz(alpha ) * roty(beta) * rotx(gamma);
(1)rpy=tr2rpy( R );
%旋转矩阵用roll-pitch-yaw角表示。
(2)R=rpy2r(alpha,beta,gamma);
%将roll-pitch-yaw角用旋转矩阵表示。
示例:
R5=rotz(0.3)*roty(0.2)*rotx(0.1)
R6=rpy2r(0.1,0.2,0.3)
rpy=tr2rpy(R5)
2.3 等效轴角坐标系法
(1)[theta,vec]=tr2angvec( R );
%求出用等效轴角坐标系法表示旋转时,旋转矩阵R对应的旋转矢量vec和转角theta。
(2)R=angvec2r(theta,vec);
%从角度和向量,计算出相应的旋转矩阵。
示例:
[theta,vec]=tr2angvec(R7)
R8=angvec2r(theta,vec)
2.4 四元数表示法
(1)Q=Quaternion([s,v]);
%建立s四元数。
(2)Q=UnitQuaternion([s,v]);
%监理单位四元数。
(3)Qi=Q.inv();
%四元数的共轭。
(4)Q.display();
%打印出可读形式。
(5)Q.plot();
%绘制四元数所指方向。
(6)Q.animate(options);
%四元数代表坐标变换的动画。
(7)R=Q.R;
%转换成3*3的旋转矩阵。
(8)T=Q.T;
%转换成4*4齐次变换矩阵。
(9)rpy=Q.torpy();
%转换成导航角。
(10)eul=Q.toeul();
%转换成欧拉角。
例子:
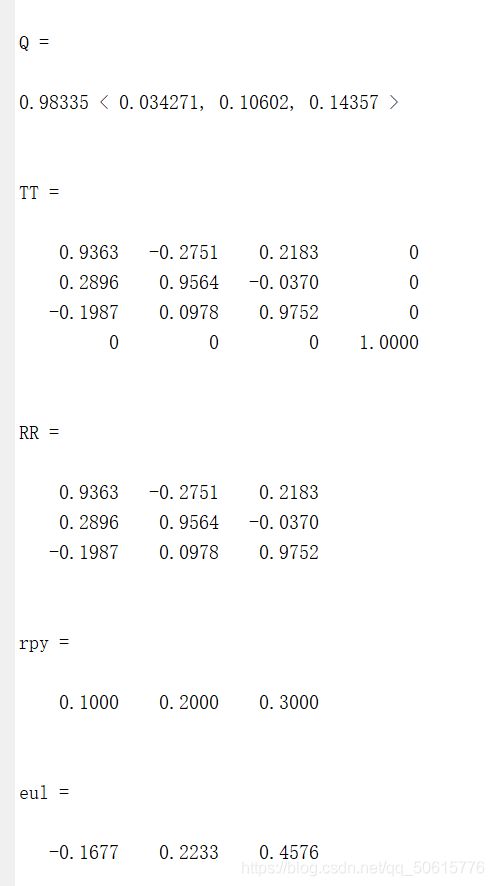
s=0.98335
v=[0.034271,0.10602,0.14357]
Q=UnitQuaternion(s,v)
q=Q.inv()
Q.display()
Q.plot()
Q.animate()
TT=Q.T
RR=Q.R
rpy=Q.torpy()
eul=Q.toeul()