扩展卡尔曼滤波（EKF）原理分析并使用Python程序估计锂离子电池SOC

        新能源汽车动力电池的 SOC 相当于普通燃油汽车的油表示数， SOC 作为能量管理的重要决策因素之一，对于优化整车能量管理、提高动力电池容量和能量利用率、防止动力电池过充电和过放电、保障动力电池在使用过程中的安全性和长寿命等起着重要作用。

       下面来介绍下基于模型的估计方法。

原理介绍

       该方法利用模型和状态估计算法完成动力电池的 SOC 估计，因此该方法首先需要建立可靠的性能模型，本章主要以等效电路模型为例介绍基于模型的动力电池 SOC 估计方法。基于建立的动力电池等效电路模型及其状态方程，应用滤波算法和观测器，搭建基于模型的 SOC 估计算法框架，具体实施流程如图1所示，包括：

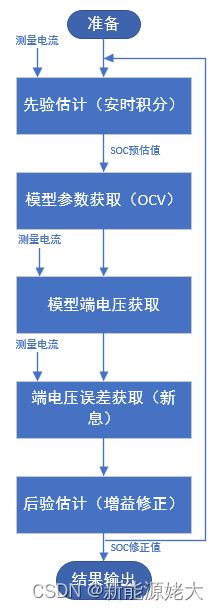
        ①基于上一时刻的 SOC 值或初始 SOC 与电流测量值，利用安时积分来计算当前时刻的 SOC 预估值。
       ②基于模型参数﹣ SOC 关系式计算此时模型参数值，如 OCV - SOC 关系。③基于模型端电压﹣参数关系式计算此时模型端电压。
       ④基于电压测量值，获取模型端电压误差，即新的信息，简称新息。
       ⑤以新息的一定增益（倍率）来修正上述 SOC 预估值，从而获取最终的 SOC 修正值，并将其用于下一时刻的输入。
步骤⑤中增益的表达形式取决于所采用的状态估计算法。显然，基于模型的方法是一种闭环的方法，它通过不断地修正 SOC 估计值，使得算法具有一定的鲁棒性。

       一般来说，基于模型的方法估计精度由预估过程与修正过程两部分共同决定，当信任安时积分的估计结果（ SOC 预估值较准）时，可适当地减小增益修正；否则应增大增益修正。但是过大的修正会使得 SOC 值波动剧烈，具体应该根据实际情况调整。
      基于模型的估计方法的性能同时取决于模型与状态估计算法两者的性能。卡尔曼滤波（Kalman Filter , KF ）类算法是动力电池 SOC 估计中使用最多的算法。 KF是由美国学者Kalman在20世纪60年代初提出的一种最小方差意义上的最优估计方法。它提供了直接处理随机噪声干扰的解决方案，将参数误差看作噪声以及把预估计量作为空间状态变量，充分利用测量数据，用递推法将系统及随机测量噪声滤掉，得到准确的空间状态值。但是，最初的KF仅适用于线性系统，扩展卡尔曼滤波算法（Extended Kalman Filter , EKF）的提出使其推广到了非线性系统。EKF应用泰勒展开将动力电池模型线性化，但在线性化的过程中会带来截断误差，进而增大 SOC 估计误差，在某些初值设置不当的情况下甚至造成发散。为此，需要对动力电池模型进行改进和优化，或者使用改进后的卡尔曼滤波算法提高状态估计系统的精度和鲁棒性。

       本篇文章使用扩展卡尔曼滤波来估计电池SOC，并给出Python代码及仿真结果分析。

Python源码

       首先是函数及数据的插入：

from battery import Battery
from kalman import ExtendedKalmanFilter as EKF
from protocol import launch_experiment_protocol
import numpy as np
import math as m

        自定义的扩展卡尔曼的算法程序，输入参数为：R0、R1、C1、std_dev、time_step

def get_EKF(R0, R1, C1, std_dev, time_step):
    # initial state (SoC is intentionally set to a wrong value)
    # x = [[SoC], [RC voltage]]
    x = np.matrix([[0.5],\
                   [0.0]])

    exp_coeff = m.exp(-time_step/(C1*R1))
    
    # state transition model
    F = np.matrix([[1, 0        ],\
                   [0, exp_coeff]])

    # control-input model
    B = np.matrix([[-time_step/(Q_tot * 3600)],\
                   [ R1*(1-exp_coeff)]])

    # variance from std_dev
    var = std_dev ** 2

    # measurement noise
    R = var

    # state covariance
    P = np.matrix([[var, 0],\
                   [0, var]])

    # process noise covariance matrix
    Q = np.matrix([[var/50, 0],\
                   [0, var/50]])

    def HJacobian(x):
        return np.matrix([[battery_simulation.OCV_model.deriv(x[0,0]), -1]])

    def Hx(x):
        return battery_simulation.OCV_model(x[0,0]) - x[1,0]

    return EKF(x, F, B, P, Q, R, Hx, HJacobian)

        对仿真结果进行绘图：

def plot_everything(time, true_voltage, mes_voltage, true_SoC, estim_SoC, current):
    import matplotlib.pyplot as plt

    fig = plt.figure(figsize = (10,10))
    ax1 = fig.add_subplot(311)
    ax2 = fig.add_subplot(312)
    ax3 = fig.add_subplot(313)

    # title, labels
    ax1.set_title('')    
    ax1.set_xlabel('Time / s')
    ax1.set_ylabel('voltage / V')
    ax2.set_xlabel('Time / s')
    ax2.set_ylabel('Soc')
    ax3.set_xlabel('Time / s')
    ax3.set_ylabel('Current / A')


    ax1.plot(time, true_voltage, label="True voltage")
    ax1.plot(time, mes_voltage, label="Measured voltage")
    ax2.plot(time, true_SoC, label="True SoC")
    ax2.plot(time, estim_SoC, label="Estimated SoC")
    ax3.plot(time, current, label="Current")
    
    ax1.legend()
    ax2.legend()
    ax3.legend()
    fig.tight_layout()
    plt.show()

if __name__ == '__main__':
    # total capacity
    Q_tot = 3.2
    
    # Thevenin model values
    R0 = 1
    R1 = 1
    C1 = 3
    
    # time period
    time_step = 10

    battery_simulation = Battery(Q_tot, R0, R1, C1)

    # discharged battery
    battery_simulation.actual_capacity = 0
    
    # measurement noise standard deviation
    std_dev = 0.015

    #get configured EKF
    Kf = get_EKF(R0, R1, C1, std_dev, time_step)

    #initialization
    time         = [0]
    true_SoC     = [battery_simulation.state_of_charge]
    estim_SoC    = [Kf.x[0,0]]
    true_voltage = [battery_simulation.voltage]
    mes_voltage  = [battery_simulation.voltage + np.random.normal(0,0.1,1)[0]]
    current      = [battery_simulation.current]

def update_all(actual_current):
        battery_simulation.current = actual_current
        battery_simulation.update(time_step)

        time.append(time[-1]+time_step)
        current.append(actual_current)

        true_voltage.append(battery_simulation.voltage)
        mes_voltage.append(battery_simulation.voltage + np.random.normal(0, std_dev, 1)[0])
        
        Kf.predict(u=actual_current)
        Kf.update(mes_voltage[-1] + R0 * actual_current)
        
        true_SoC.append(battery_simulation.state_of_charge)
        estim_SoC.append(Kf.x[0,0])
        
        return battery_simulation.voltage #mes_voltage[-1]
    
    # launch experiment
    launch_experiment_protocol(Q_tot, time_step, update_all)

    # plot stuff
    plot_everything(time, true_voltage, mes_voltage, true_SoC, estim_SoC, current)

        仿真结果：

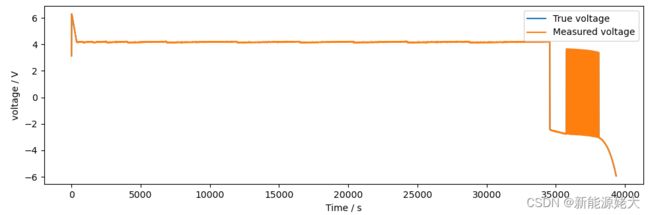
       1.真实电压值与测量的电压值的对比：

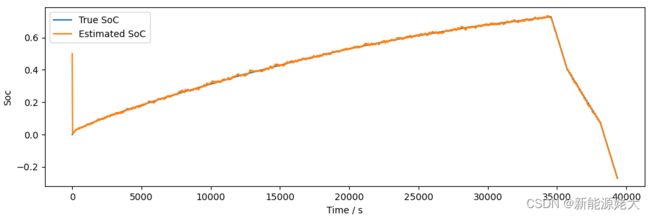
        2.真实的SOC与扩展卡尔曼滤波估计出的SOC进行对比：

        3.电流的变化曲线

       硕博期间所有的程序代码，一共2个多g，可以给你指导，赠送半个小时的语音电话答疑。电池数据+辨识程序+各种卡尔曼滤波算法都在里面了，后续还会有新模型的更新。快速入门BMS软件。某鹅：2629471989

 参考书籍：《动力电池管理系统核心算法》