佳木斯集训Day3例题 数论

· 今天依旧是数论…专题是组合数、扩展欧几里得、逆元
上题

Ralph And His Magic Field（cf894B）

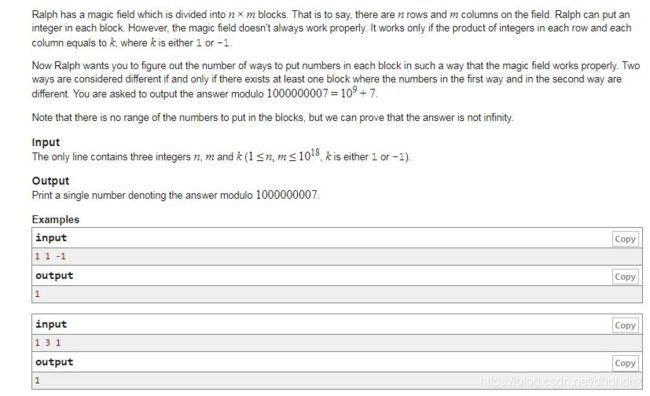
题目大意:

思路非常清晰 $(n-1)\ast (m-1)$随便填 最后一行补$1$或$-1$让结果为k
需要注意的是 当$n、m$一奇一偶且$k=-1$时 无解输出$-1$
很好证明:假设 当$n、m$一奇一偶且$k=-1$时有解 。不妨设$n$为奇数$m$为偶数
因为$k=-1$所以 $n$行每行有奇数个$-1$由于有 $m$行 $m$为偶数 所以整个矩阵有偶数个$-1$
同理$m$行每行有奇数个$-1$ $n$行 $n$为奇数 所以整个矩阵有奇数个$-1$ 矛盾
所以当$n、m$一奇一偶且$k=-1$时 无解
上代码

#include
typedef long long ll;
const ll mod=1000000007;
ll n,m,k;
ll quickpow(ll x, ll y)
{
    ll re=1;
    while(y)
    {
        if(y&1)(re*=x)%=mod;
        (x*=x)%=mod;y>>=1;
    }
    return re%mod;
}
int main()
{
    scanf("%lld%lld%lld",&n,&m,&k);
    if((m+n)&1&&k==-1)
    {
        puts("0");
        return 0;
    }
    if(n==1||m==1)
    {
        puts("1");
        return 0;
    }
    (n-=1)%=(mod-1);
    (m-=1)%=(mod-1);
    printf("%lld\n",quickpow(2,n*m));
}

[Shoi2017]组合数问题

样例输入
2 10007 2 0
样例输出
8

震惊!上海省选竟然出如此水的题!
所求的式子为${\sum }_{i=0}^{\infty }\left(\genfrac{}{}{0ex}{}{nk}{ik+r}\right)$
显然无穷是骗人的 因为当m>n时 $\left(\genfrac{}{}{0ex}{}{n}{m}\right)=0$
观察式子可发现 原式可化为:${\sum }_{j\equiv r(\mathrm{m}\mathrm{o}\mathrm{d}k)}\left(\genfrac{}{}{0ex}{}{nk}{j}\right)$
其实际意义为 从$n\times k$个物品中选取模$k$为$r$个物品
设从$n$个物品中选取模$k$为$r$个物品的方案数为$F(n,r)$
那么$F(i,j)=F(i-1,j)+F(n-1,(n-1+k)modk)$
这显然是一道披着组合数外套的矩阵乘法
注意一定要将矩阵清零!!!
直接上代码

#include
#include
using namespace std;
typedef long long ll;
struct node
{
    ll sqr[51][51];
    node()
    {
        memset(sqr,0,sizeof(sqr));
    }
};
node f,x,re;
ll n;
int p,r,k;
node operator *(const node &a, const node &b)
{
    node c;
    for(int i=0;i<k;i++)for(int j=0;j<k;j++)for(int l=0;l<k;l++)
        c.sqr[i][j]=(c.sqr[i][j]+a.sqr[i][l]*b.sqr[l][j]%p)%p;
    return c;
}
int main()
{
    scanf("%lld%d%d%d",&n,&p,&k,&r);
    f.sqr[0][0]=1;
    for(int i=0;i<k;i++)
    {
        x.sqr[(i-1+k)%k][i]++;
        x.sqr[i][i]++;
        re.sqr[i][i]=1;
    }
    n*=k;
    while(n)
    {
        if(n&1)re=re*x;
        x=x*x;
        n>>=1;
    }
    printf("%lld\n",(f*re).sqr[0][r]);
}

Count Pairs (CodeForces - 1189E )

题目描述



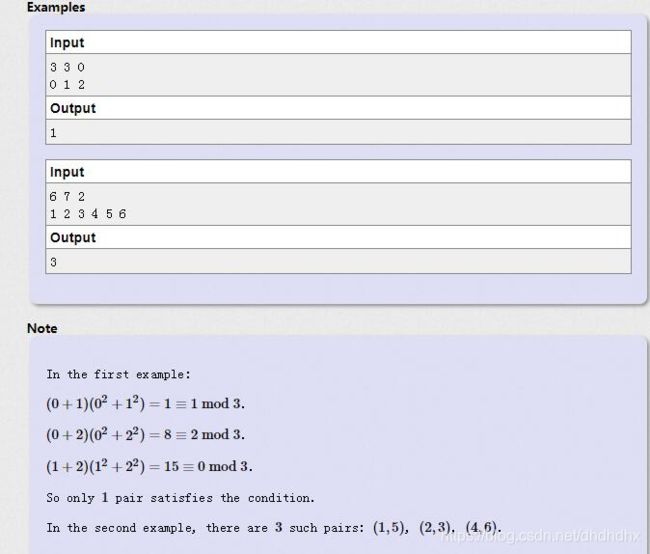
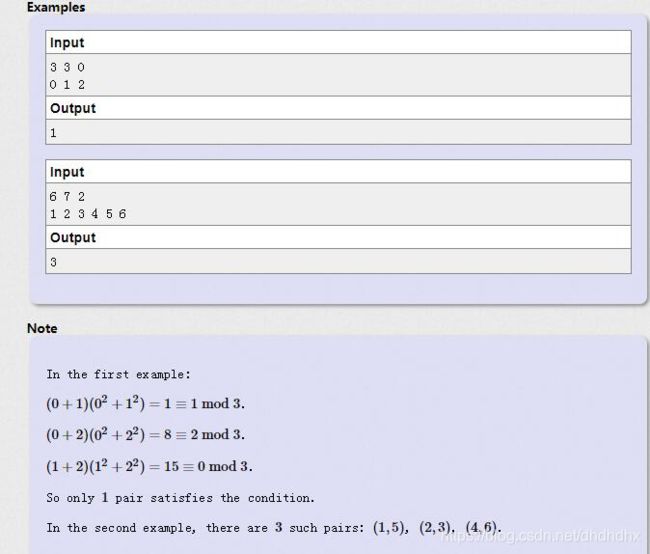
翻译题面如下:

首先我们非常快的可以发现
$(a_i+a_j)(a_i^2+a_j^2)\equiv k(\mathrm{m}\mathrm{o}\mathrm{d}p)$
$\iff (a_i-a_j)(a_i+a_j)(a_i^2+a_j^2)\equiv k(a_i-a_j)(\mathrm{m}\mathrm{o}\mathrm{d}p)$
$\iff (a_i^2-a_j^2)(a_i^2+a_j^2)\equiv k(a_i-a_j)(\mathrm{m}\mathrm{o}\mathrm{d}p)$
$\iff (a_i^4-a_j^4)\equiv k(a_i-a_j)(\mathrm{m}\mathrm{o}\mathrm{d}p)$
$\iff a_i^4-k\cdot a_i\equiv a_j^4-k\cdot a_j(\mathrm{m}\mathrm{o}\mathrm{d}p)$
所以这道题就转化为求数列$b_i=a_i^4-k\cdot a_{i}modp$a中相同元素的个数
排个序算一下就好咯
上代码

#include
#include
using namespace std;
typedef long long ll;
inline void read(ll &x)
{
    ll s=0;char ch=getchar();
    while(ch<'0'||ch>'9')ch=getchar();
    while(ch>='0'&&ch<='9'){s=(s<<3)+(s<<1)+(ch&15);ch=getchar();}
    x=s;
}
ll n,p,k,ans,now,a[300001];
int main()
{
    read(n);read(p);read(k);
    for(ll i=1;i<=n;i++)
    {
        read(a[i]);
        a[i]=(a[i]*a[i]%p*a[i]%p*a[i]%p-k*a[i]%p+p)%p;
    }
    sort(a+1,a+1+n);
    for(ll i=2;i<=n;i++)
    {
        if(a[i-1]==a[i])now++,ans+=now;
        else now=0;
    }
    printf("%lld\n",ans);
}

Magic Stones（cf1110e）

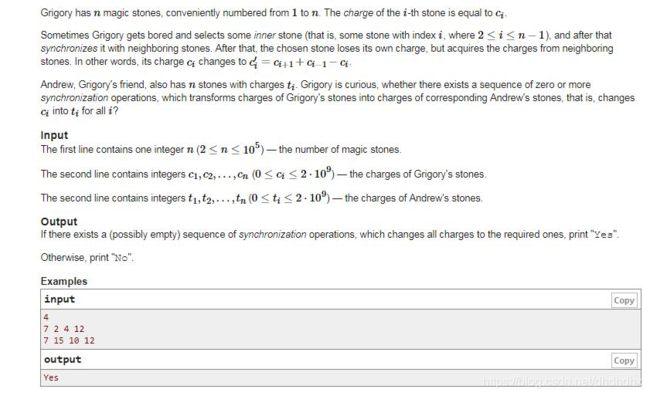
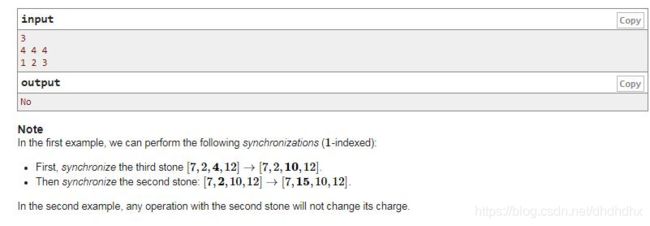
翻译题面如下:

修改后的$c_i=c_{i+1}+c_{i-1}-c_i$ 设$d(i)$为$c(i)$的差分数组 则有:
$d(i+1)=c_{i+1}-c_i^{’}=c_{i+1}-c_{i+1}-c_{i-1}+ci=c_i-c_{i-1}=d(i)$
$d(i)=c_i^{’}-c_{i-1}=c_{i+1}+c_{i-1}-c_i-c_{i-1}=c_{i+1}-c_i=d(i+1)$
显然调换了$d(i+1)$和$d(i)$
所以只需要判断$d(i)$是否出现在$t$数组的差分数组就好咯
但需要特判$c(1),c(n)$是否等于$t(1),t(n)$
上代码

#include
#include
using namespace std;
inline void read(int &x)
{
    int s=0,w=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){s=(s<<3)+(s<<1)+(ch&15);ch=getchar();}
    x=s*w;
}
int n,x,y,c[100001],d[100001],t[100001],u[100001];
int main()
{
    read(n);
    for(int i=1;i<=n;i++)
    {
        read(c[i]);
        d[i]=c[i]-c[i-1];
    }
    for(int i=1;i<=n;i++)
    {
        read(t[i]);
        u[i]=t[i]-t[i-1];
    }
    if(c[1]!=t[1]||c[n]!=t[n])
    {
        puts("No");
        return 0;
    }
    sort(d+2,d+1+n);sort(u+2,u+1+n);
    for(int i=2;i<=n;i++)
    {
        if(d[i]!=u[i])
        {
            puts("No");
            return 0;
        }
    }
    puts("Yes");
}

《瞿葩的数字游戏》T3-三角圣地

题目描述
题目背景: 国王1带大家到了数字王国的中心：三角圣地。
不是说三角形是最稳定的图形嘛，数字王国的中心便是由一个倒三角构成。这个倒三角的顶端有一排数字，分别是1_N。1N可以交换位置。之后的每一行的数字都是上一行相邻两个数字相加得到的。这样下来，最底端就是一个比较大的数字啦！数字王国称这个数字为“基”。国王1希望“基”越大越好，可是每次都自己去做加法太繁琐了，他希望你能帮他通过编程计算出这个数的最大值。但是这个值可能很大，所以请你输出它mod 10007 的结果。
任务：给定N，求三角形1~N的基的最大值 再去 mod 10007。
输入
一个整数N
输出
一个整数，表示1~N构成的三角形的最大的“基”
样例输入
【样例 1 输入】
4
【样例 2 输入】
1125
样例输出
【样例 1 输出】
24
【样例 2 输出】
700
提示
数据：
20% 0<=N<=100
50% 0<=N<=3000
100% 0<=N<=1000000
样例解释：
1 3 4 2
4 7 6
11 13
24 是N=4的时候的最大值，当然还有别的构成形式。
PS：它叫做三角圣地，其实它就是个三角形~
本题数据已经更新，目前全部正确无误！
不要面向数据编程！ ok本题正解打表
我们以4为例 设第一层的4个数为$a$, $b$ ,$c$ ,$d$
则 第二层为$a+b$ ,$b+c$ ,$c+d$
第三层为 $a+2b+c$ ,$b+2c+d$
基数为$a+3b+3c+d$
首先我们一定要让$ad$最小 $bc$最大 其次 有没有发现这个$1$ $3$ $3$ $1$好熟悉!
没错 这就是二项式定理 杨辉三角中的$1$ $3$ $3$ $1$
直接求一圈${\sum }_{i=1}^n\left(\genfrac{}{}{0ex}{}{n-1}{i-1}\right)\times (i)$就好啦
但是本题的$mod$小的亚批 直接用逆元你就跪啦 这也就是为什么我 Day3题解中写随机设$mod$设小就跪了的原因 所以我们需要用$Lucas$定理
请见代码

#include
typedef long long ll;
inline void read(ll &x)
{
    ll s=0,w=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){s=(s<<3)+(s<<1)+(ch&15);ch=getchar();}
    x=s*w;
}
const ll mod=10007,N=1000000;
ll fac[N],facinv[N],inv[N],ans=3,n;
ll C(ll n, ll m){return fac[n]*facinv[m]%mod*facinv[n-m]%mod;}
ll lucas(ll n, ll m){return n<mod&&m<mod?C(n,m):C(n%mod,m%mod)*lucas(n/mod,m/mod)%mod;}
int main()
{
    read(n);
    inv[1]=fac[0]=fac[1]=facinv[1]=facinv[0]=1;
    for(int i=2;i<=mod;i++)
    {
        inv[i]=(mod-mod/i)*inv[mod%i]%mod;
        facinv[i]=facinv[i-1]*inv[i]%mod;
        fac[i]=fac[i-1]*i%mod;
    }
    for(int i=2;i<n+1>>1;i++)(ans+=lucas(n-1,i-1)*(4*i-1))%=mod;
    if(n&1)(ans+=lucas(n-1,n>>1)*n)%=mod;
    else (ans+=lucas(n-1,(n>>1)-1)*((n<<1)-1))%=mod;
    printf("%lld\n",ans);
}

这就是今天的例题 如果有问题可以发到评论区或者加$QQ407694747$我们一起讨论
各位大佬各路神犇请多指教