基于Yolo3_deep_sort的目标追踪(原理及部分代码说明) --- 已解决
基于Yolo3_Deep_sort的多目标追踪算法原理及部分代码说明
写在前面的话:楼主前一段时间参与了一个小项目,是关于人的目标追踪,在此记录一下,这篇博文主要是记录一下对这个方法的认识和理解,希望能引起你的共鸣。如果想看具体的测试环境搭建及复现说明,请查看我的另一篇博客,传送门。
将Yolo3与Deep_sort相结合,相当于目标检测中的Two stages的结构,采用detection(Yolo3)+ track(Deep_sort)的方式实现目标追踪。
1、Yolo算法思想
Yolo(You Only Look Once,Yolo)在本方法中负责detection部分,其将输入图像分成S×S个格子,若某个物体 Ground truth 的中心位置的坐标落入到某个格子,那么这个格子就负责检测出这个物体,如图1所示。
(1) Yolo1采用卷积神经网络结构
开始的卷积层提取图像特征,全连接层预测输出概率。借鉴了GoogLeNet分类网络结构,共有24个卷积层,2个全链接层,网络在最后使用全连接层进行类别输出。
损失函数:使用了均方和误差作为loss函数:
l o s s = ∑ i = 0 s 2 c o o r d E r r + i o u E r r + c l s E r r loss=\sum_{i=0}^{s^{2}}coordErr+iouErr+clsErr loss=i=0∑s2coordErr+iouErr+clsErr
其由三部分组成:坐标误差、IOU误差和分类误差。
(2) Yolo2相对Yolo1进行了改进
首先去掉了在定位层后的dropout层,并在卷积层中全部使用BN层进行批量归一化处理。借鉴Faster R-CNN的思想预测bbox的偏移,移除了全连接层,使用box替换grid预测一个类别。
而后,对Faster R-CNN的首选先验框方法做了改进,采样k-means在训练集bbox上进行聚类产生合适的先验框,由于使用欧氏距离会使较大的bbox比较小的bbox产生更大的误差,而IOU与bbox尺寸无关,因此使用IOU参与距离计算,使得通过这些anchor boxes获得好的IOU分值。距离公式:
D ( b o x , c e n t r o i d ) = 1 − I O U ( b o x , c e n t r o i d ) D(box,centroid)=1-IOU(box,centroid) D(box,centroid)=1−IOU(box,centroid)
其聚类过程主要是将每个bbox的宽和高相对整张图片的比例(Wr,Hr)进行聚类,得到k个anchor box的过程。
最后,其进行了特征融合,融合了低语义层的信息来检测小目标物体Faster R-CNN和SSD均使用了不同的feature map以适应不同尺度大小的目标。YOLO2使用了一种不同的方法,添加一个pass through layer,把浅层特征图(26×26)连接到深层特征图(连接到新加入的三个卷积核尺寸为3 × 3的卷积层最后一层的输入)。通过叠加浅层特征图相邻特征到不同通道(而非空间位置),类似于Resnet中的identity mapping。这个方法把26×26×512的特征图叠加成13×13×2048的特征图,与原生的深层特征图相连接,使模型有了细粒度特征。
(3) Yolo3相对Yolo2进行了改进
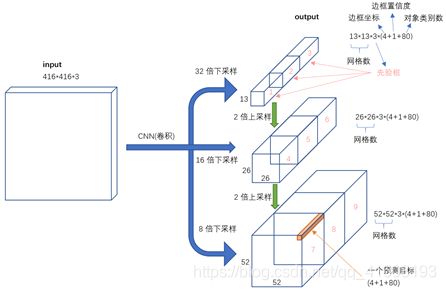
最为明显的改变是网络的结构由Darknet-19变为Darknet-53。可实现多尺度预测,其输出有3层,分别为13×13、26×26、52×52,意味着分别做3次预测,可让网络同时学习到深层和浅层的特征,通过叠加浅层特征图特征到相邻通道,类似于FPN中的umsample+concat。这个方法把26×26×512的特征图叠加13×13×256的特征图,使模型有了细粒度特征,增加对小目标的识别能力。其输入到输出的映射关系图如图2所示。
2、Deep_sort算法思想
Deep_sort算法在本项目中负责track阶段,即经Yolo3检测出bbox后,负责对每一帧图像中的bbox进行匹配跟踪。
(1) sort算法(在track之前已经完成了detection)
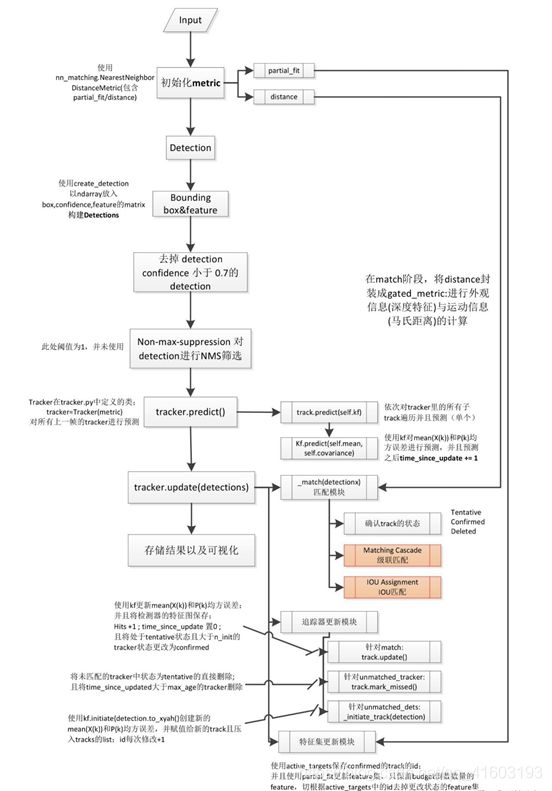
首先当第一帧图像进入时,以检测到的目标初始化并创建新的tracker,标注id,而后图像输入时经Kalman Filter计算出前面帧中bbox产生的状态预测和协方差预测,而后求取tracker所有目标状态与本帧检测的bbox的IOU,通过Hungarian Algorithm得到IOU最大的唯一匹配,即(track, detection)匹配对,去掉匹配值小于iou_threshold的匹配对。而后使用本帧中匹配到的目标检测bbox去更新Kalman Filter,计算Kalman gain、状态更新和协方差更新,并将状态更新输出作为本帧跟踪的bbox,此外,对本帧中没有匹配到的目标重新初始化tracker,这之中,Kalman Tracker联合了历史跟踪记录,调节历史box与本帧box的残差,更好的匹配跟踪id。
Ps:
Kalman Filter:可用于对目标的轨迹进行预测,并用置信度较高的跟踪结果进行预测结果的修正。
Hungarian Algorithm:是一种寻找二分图的最大匹配的算法,在多目标检测跟踪问题中可以理解为:寻找前后两帧的若干目标的匹配最优解的方法。
(2) Deep_sort算法(对sort算法的改进)
Sort算法使用简单的卡尔曼滤波处理逐帧数据的关联性以及使用匈牙利算法进行关联度量,这种简单的算法在高帧速率下获得了良好的性能。但由于Sort忽略了被检测物体的表面特征,因此只有在物体状态估计不确定性较低是才会准确,在Deep SORT中,使用更加可靠的度量来代替关联度量,增加了网络对遗失和障碍的鲁棒性。
1) 关联度量(Association Metric)
使用马氏距离计算物体检测bbox dj和物体跟踪bbox yi 之间的距离:
d ( 1 ) ( i , j ) = ( d j + y i ) T S i − 1 ( d j − y i ) d^{(1)}(i,j)=(d_{j}+y_{i})^{T}S^{-1}_{i}(d_{j}-y_{i}) d(1)(i,j)=(dj+yi)TSi−1(dj−yi) 不使用欧式距离的原因是dj和yi 的空间域分布不同,欧式距离忽略空间域分布的计算结果,不能准确反映两者的真实距离。当两者距离≤特定阈值,则表示两者关联,其表示方式为:
b i , j ( 1 ) = I [ d ( 1 ) ( i , j ) ≤ t ( 1 ) ] b^{(1)}_{i,j}=\mathbb{I}\left [ d^{(1)}(i,j)\leq t^{(1)} \right] bi,j(1)=I[d(1)(i,j)≤t(1)] 但马氏距离依然不能很好的解决物体被长时间遮挡后关联不正确导致id switch的问题。
对于跟踪器i,为它创建一个集合 保留它过去Lk次成功跟踪后物体检测bbox对应的Lk个Feature的向量集合,当第i个物体跟踪的所有Feature向量和第j个物体检测之间的最小余弦距离≤特定阈值时,则表示两者关联,最小余弦距离和关联表示计算公式为:
d ( 2 ) ( i , j ) = m i n { 1 − r j T r k ( i ) ∣ r k ( i ) ∈ R i } d^{(2)}(i,j)=min\left\{ 1-r^{T}_{j}r^{(i)}_{k}|r^{(i)}_{k} \in R_{i} \right\} d(2)(i,j)=min{1−rjTrk(i)∣rk(i)∈Ri} b i , j ( 2 ) = I [ d ( 2 ) ( i , j ) ≤ t ( 2 ) ] b^{(2)}_{i,j}=\mathbb{I}[d^{(2)}(i,j)\leq t^{(2)}] bi,j(2)=I[d(2)(i,j)≤t(2)] 因此得到新的关联度量公式为:
c i , j = λ d ( 1 ) ( i , j ) + ( 1 + λ ) d ( 2 ) ( i , j ) c_{i,j}=\lambda d^{(1)}(i,j)+(1+\lambda) d^{(2)}(i,j) ci,j=λd(1)(i,j)+(1+λ)d(2)(i,j) 组合距离阈值判断不等式,作为总的判断第i个物体跟踪和第j个物体检测之间的距离(关联度量)是否关联的总公式:
b i , j = ∏ m = 1 2 b i , j ( m ) b_{i,j}=\prod_{m=1}^{2}b^{(m)}_{i,j} bi,j=m=1∏2bi,j(m)
2) 关联算法(Matching Cascade)

其中:
T:物体跟踪集合;
D:物体检测集合;
1. C矩阵存放所有物体跟踪i与物体检测j之间距离的计算结果;
2. B矩阵存放所有物体跟踪i与物体检测j之间是否关联的判断(0/1);
3. 关联集合M初始化维{};
4. 将找不到匹配的检测物体集合初始化为{};
5. 从刚刚匹配成功的跟踪器循环遍历到最多已经有Amax次没有匹配的跟踪器;
6. 选择满足条件的跟踪器集合Tn;
7. 根据最小成本计算法计算出Tn与检测物体j关联成功产生集合[xi,j];
8. 更新M为匹配成功的(跟踪物体i,检测物体j)集合;
9. 从U中去除已经匹配成功的检测物体j;
10. 循环;
11. 返回M U两个集合。
3) 原理图,如图4所示。
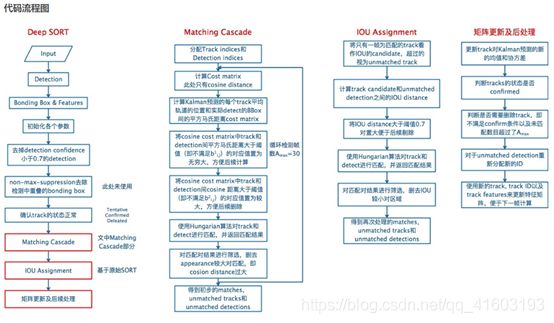
3、Yolo3_Deep_sor算法
将Deep_sort算法中的detection部分换成Yolo3算法,总结成为图5所示流程图:
相关代码解释:
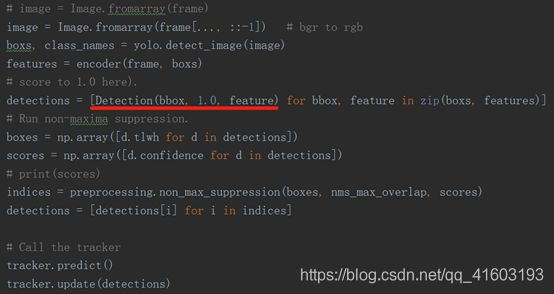
(1) Detection
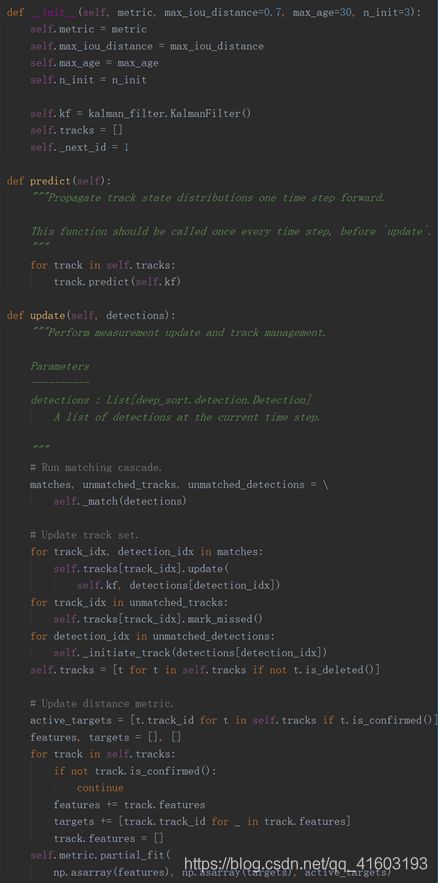
(2) tracker
是Tracker类的一个对象,实现跟踪器功能,可以根据检测到的detections,进行匹配、筛选、更新等操作:
(3) track
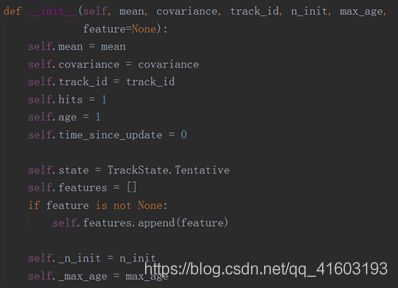
是Track类的一个对象,每个Tracker里面包含一个tracks列表,列表的每个元素是Track的一个对象,它的属性是根据单个detection生成的均值、方差、id等等,为一个跟踪器里面的多个跟踪目标。
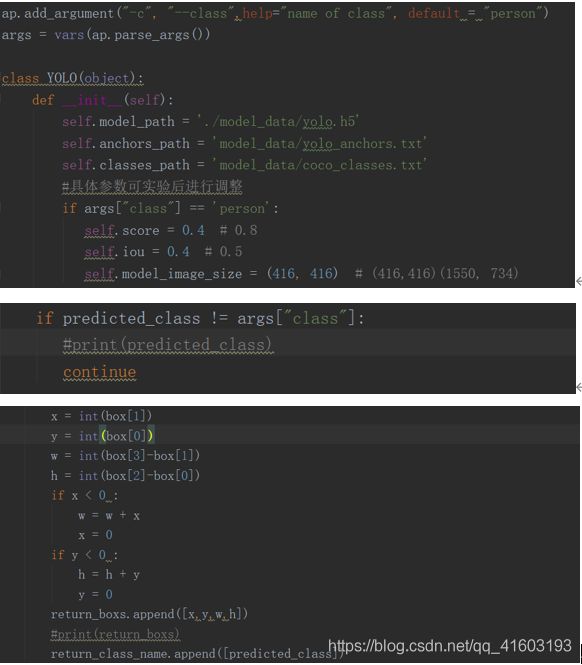
(4) 检测类别(Yolo3)
(5) 卡尔曼滤波(deep_sort)
我们可以理解为,根据当前的仪器"测量值" 和上一刻的 “预测量” 和 “误差”,计算得到当前的最优量, 再预测下一刻的量。可用于对目标的轨迹进行预测,并使用置信度较高的跟踪结果对预测结果进行修正。
传送门:这篇文章对卡尔曼滤波进行了较为详尽的解释。
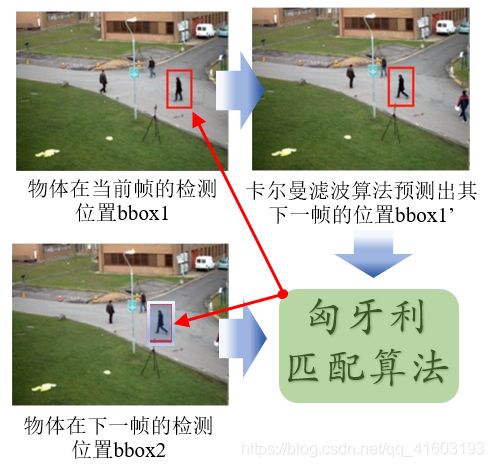
(6) 匈牙利匹配(deep_sort)
我们可以理解为,为了找到最优的匹配结果,所付出的代价最小的一个算法。将前一帧中的跟踪框tracks与当前帧中的检测框detections进行关联,通过外观信息(appearance information)和马氏距离(Mahalanobis distance),或者IOU来计算代价矩阵。可寻找前后 2 帧的若干目标的匹配的最优解。
传送门:这篇文对匈牙利匹配进行了较为详细的解释。
效果展示
对算法的理解和介绍简单讲到这里,希望能引起你的共鸣,对你有所帮助,关于算法的部署和链接在我的另一篇博客,稍后会更新!