PyTorch执行矩阵求导详细过程
本文目录
-
- 一、数学形式
-
- 1. 矩阵求导
- 2. 非矩阵求导
- 二、PyTorch
- 三、执行代码
本文用最小二乘法来简述PyTorch中的梯度下降具体执行过程
之前已经推到过最小二乘法的矩阵求导过程:链接
一、数学形式
之前虽然知道矩阵求导是怎么来的,但是具体PyTorch是怎么实现的还未知,所以这里进行了求解和验证,采用了SGD梯度下降,为方便计算,batch_size=3,并且采用一元线性回归来实现,所以这里w只有一维,带有bias偏置
数学表达式为
Y = X w + b Y = Xw+b Y=Xw+b
Y = ( y 1 y 2 . . . y n ) n × 1 X = ( x 1 T x 2 T . . . x n T ) n × p w = ( w 1 w 2 . . . w n ) p × 1 Y = \begin{pmatrix} y_{1} \\ y_{2} \\ ... \\ y_{n} \end{pmatrix}_{n\times 1}~~~ X = \begin{pmatrix} x_{1}^{T} \\ x_{2}^{T} \\ ... \\ x_{n}^{T} \end{pmatrix}_{n\times p}~~~ w = \begin{pmatrix} w_{1} \\ w_{2} \\ ... \\ w_{n} \end{pmatrix}_{p\times 1} Y=⎝⎜⎜⎛y1y2...yn⎠⎟⎟⎞n×1 X=⎝⎜⎜⎛x1Tx2T...xnT⎠⎟⎟⎞n×p w=⎝⎜⎜⎛w1w2...wn⎠⎟⎟⎞p×1
注意为了方便下面验证,取一元线性回归,即参数
Y = ( y 1 y 2 . . . y n ) n × 1 X = ( x 1 T x 2 T . . . x n T ) n × 1 → ( x 1 x 2 . . . x n ) n × 1 w = ( w ) 1 × 1 Y = \begin{pmatrix} y_{1} \\ y_{2} \\ ... \\ y_{n} \end{pmatrix}_{n\times 1}~~~ X = \begin{pmatrix} x_{1}^{T} \\ x_{2}^{T} \\ ... \\ x_{n}^{T} \end{pmatrix}_{n\times 1} \rightarrow \begin{pmatrix} x_{1} \\ x_{2} \\ ... \\ x_{n} \end{pmatrix}_{n\times 1}~~~ w = \begin{pmatrix} w \end{pmatrix}_{1\times 1} Y=⎝⎜⎜⎛y1y2...yn⎠⎟⎟⎞n×1 X=⎝⎜⎜⎛x1Tx2T...xnT⎠⎟⎟⎞n×1→⎝⎜⎜⎛x1x2...xn⎠⎟⎟⎞n×1 w=(w)1×1
本来 x T x^{T} xT为 1 × p 1\times p 1×p的矩阵,即n元,现在改为一元,转置相当于没变化了
接下来给出矩阵求导以及非矩阵求导的公式,这里我们取batch_size=3,即 n = 3 n=3 n=3
损失函数为:
L = 1 n ∑ i = 1 n ( y i − x i T w ) 2 L = \frac{1}{n} \sum_{i=1}^{n}(y_{i}-x_{i}^{T}w)^{2} L=n1i=1∑n(yi−xiTw)2
1. 矩阵求导
d L d w = 2 1 n X T ( X w − Y ) \frac{dL}{dw} = 2\frac{1}{n}X^{T}(Xw-Y) dwdL=2n1XT(Xw−Y)
矩阵求导的时候没有算上偏置 b b b,下面非矩阵求导会算上,而且主要是用非矩阵求导的过程来验证PyTorch运行过程,所以不影响
将 n = 3 n=3 n=3带入得
d L d w = 2 1 n X T ( X w − Y ) = 2 3 ( x 1 x 2 x 3 ) ( ( x 1 x 2 x 3 ) ( w ) − ( y 1 y 2 y 3 ) ) = 2 3 ( x 1 x 2 x 3 ) ( x 1 w − y 1 x 2 w − y 2 x 3 w − y 3 ) = 2 3 ( x 1 2 w − x 1 y 1 x 2 2 w − x 2 y 2 x 3 2 w − x 3 y 3 ) \begin{aligned} \frac{dL}{dw} & = 2\frac{1}{n}X^{T}(Xw-Y) \\ & = \frac{2}{3} \begin{pmatrix} x_{1} & x_{2} & x_{3}\end{pmatrix} ( \begin{pmatrix} x_{1} \\ x_{2} \\ x_{3}\end{pmatrix} \begin{pmatrix} w \end{pmatrix} - \begin{pmatrix} y_{1} \\ y_{2} \\ y_{3}\end{pmatrix} ) \\ & = \frac{2}{3} \begin{pmatrix} x_{1} & x_{2} & x_{3}\end{pmatrix} \begin{pmatrix} x_{1}w-y_{1} \\ x_{2}w-y_{2} \\ x_{3}w-y_{3}\end{pmatrix} \\ & = \frac{2}{3} \begin{pmatrix} x_{1}^{2}w-x_{1}y_{1} \\ x_{2}^{2}w-x_{2}y_{2} \\ x_{3}^{2}w-x_{3}y_{3}\end{pmatrix} \end{aligned} dwdL=2n1XT(Xw−Y)=32(x1x2x3)(⎝⎛x1x2x3⎠⎞(w)−⎝⎛y1y2y3⎠⎞)=32(x1x2x3)⎝⎛x1w−y1x2w−y2x3w−y3⎠⎞=32⎝⎛x12w−x1y1x22w−x2y2x32w−x3y3⎠⎞
2. 非矩阵求导
d L d w = 2 1 n ( w ∑ i = 1 n x i 2 − ∑ i = 1 n ( y i − b ) x i ) \frac{dL}{dw} = 2\frac{1}{n}(w\sum_{i=1}^{n}x_{i}^{2} - \sum_{i=1}^{n}(y_{i}-b)x_{i}) dwdL=2n1(wi=1∑nxi2−i=1∑n(yi−b)xi)
将 n = 3 n=3 n=3带入得
d L d w = 2 1 n ( w ∑ i = 1 n x i 2 − ∑ i = 1 n ( y i − b ) x i ) = 2 3 ( w ( x 1 2 + x 2 2 + x 3 2 ) − [ ( ( y 1 − b ) x 1 ) + ( ( y 2 − b ) x 2 ) + ( ( y 3 − b ) x 3 ) ] ) = 2 3 ( w ( x 1 2 + x 2 2 + x 3 2 ) − [ ( x 1 y 1 − x 1 b ) + ( x 2 y 2 − x 2 b ) + ( x 3 y 3 − x 3 b ) ] ) = 2 3 ( w ( x 1 2 + x 2 2 + x 3 2 ) − ( x 1 y 1 + x 2 y 2 + x 3 y 3 ) + ( x 1 b + x 2 b + x 3 b ) ) \begin{aligned} \frac{dL}{dw} & = 2\frac{1}{n}(w\sum_{i=1}^{n}x_{i}^{2} - \sum_{i=1}^{n}(y_{i}-b)x_{i}) \\ & = \frac{2}{3}(w(x_{1}^{2}+x_{2}^{2}+x_{3}^{2}) - [((y_{1}-b)x_{1})+((y_{2}-b)x_{2})+((y_{3}-b)x_{3})]) \\ & = \frac{2}{3}(w(x_{1}^{2}+x_{2}^{2}+x_{3}^{2}) - [(x_{1}y_{1}-x_{1}b)+(x_{2}y_{2}-x_{2}b)+(x_{3}y_{3}-x_{3}b)]) \\ & = \frac{2}{3}(w(x_{1}^{2}+x_{2}^{2}+x_{3}^{2}) - (x_{1}y_{1}+x_{2}y_{2}+x_{3}y_{3}) + (x_{1}b+x_{2}b+x_{3}b)) \\ \end{aligned} dwdL=2n1(wi=1∑nxi2−i=1∑n(yi−b)xi)=32(w(x12+x22+x32)−[((y1−b)x1)+((y2−b)x2)+((y3−b)x3)])=32(w(x12+x22+x32)−[(x1y1−x1b)+(x2y2−x2b)+(x3y3−x3b)])=32(w(x12+x22+x32)−(x1y1+x2y2+x3y3)+(x1b+x2b+x3b))
上述就是对 w w w求导的结果,由于 b b b相同,直接给出结果
d L d b = 2 n ( n b − ∑ i = 1 n ( y i − w x i ) ) \frac{dL}{db} = \frac{2}{n}(nb - \sum_{i=1}^{n}(y_{i} - wx_{i})) dbdL=n2(nb−i=1∑n(yi−wxi))
下面验证时仅针对有偏置 b b b的一元线性回归,并且只验证 w w w
二、PyTorch
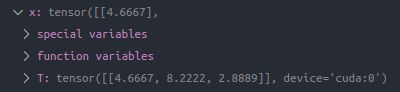
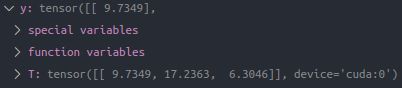
这里我们batch_size=3,随机取输入 x x x和 y y y分别为
输出为
loss为
![]()
w w w的梯度为-150.28
更新前后 w w w与 b b b的参数为
- w : − 0.34487 → − 0.19458 w: -0.34487\rightarrow -0.19458 w:−0.34487→−0.19458
- b : 0.86449 → 0.88858 b:0.86449\rightarrow 0.88858 b:0.86449→0.88858
而学习率为0.001,恰好 − 0.34487 × − [ 0.001 ∗ ( − 150.28 ) ] = − 0.19458 -0.34487\times -[0.001*(-150.28)] = -0.19458 −0.34487×−[0.001∗(−150.28)]=−0.19458

下面我们手动计算进行验证看看是否与上述输出一致
import numpy as np
x = np.array([4.6667, 8.2222, 2.8889])
y = np.array([9.7349, 17.2363, 6.3046])
y_ = np.array([-0.7449, -1.9711, -0.1318])
# 计算loss
f = y_-y
l = np.power(f, 2)
print(l)
l_ = np.sum(l)
print(l_/3)
'''
[109.82620804 368.92421476 41.42724496]
173.39255591999998
'''
# 计算相应参数
print(np.sum(x))
print(np.power(x, 2))
print(x*y)
print(np.sum(np.power(x, 2)))
print(np.sum(x*y))
'''
15.7778
[21.77808889 67.60457284 8.34574321]
[ 45.42985783 141.72030586 18.21335894]
97.72840494
205.36352263000003
'''
# 计算w梯度
gw = (2/3)*((-0.3449 * 97.7284)-(205.3635-15.7778*0.8645))
print(gw)
'''
-150.28674470666664
'''
可以发现我们的计算是一致的
三、执行代码
'''
torch.optim.SGD
'''
import os
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
from torch.utils.data import Dataset, DataLoader
# 1. 创建数据集
def create_linear_data(nums_data, if_plot=False):
"""
Create data for linear model
Args:
nums_data: how many data points that wanted
Returns:
x with shape (nums_data, 1)
"""
x = torch.linspace(2, 10, nums_data)
x = torch.unsqueeze(x,dim=1)
k = 2
y = k * x + torch.rand(x.size())
if if_plot:
plt.scatter(x.numpy(),y.numpy(),c=x.numpy())
plt.show()
# data = torch.cat([x, y], dim=1)
datax = x
datay = y
return datax, datay
datax, datay = create_linear_data(10, if_plot=False)
length = len(datax)
# 2. Dummy DataSet
class LinearDataset(Dataset):
def __init__(self, length, datax, datay):
self.len = length
self.datax = datax
self.datay = datay
def __getitem__(self, index):
datax = self.datax[index]
datay = self.datay[index]
return {'x': datax, 'y': datay}
def __len__(self):
return self.len
# 3. Parameters and DataLoaders
batch_size = 3
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
linear_loader = DataLoader(dataset=LinearDataset(length, datax, datay),
batch_size=batch_size, shuffle=True)
# 4. model
class Model(torch.nn.Module):
"""
Linear Regressoin Module, the input features and output
features are defaults both 1
"""
def __init__(self):
super().__init__()
self.linear = torch.nn.Linear(1, 1)
def forward(self, input):
output = self.linear(input)
print("In Model: #############################################")
print("input: ", input.size(), "output: ", output.size())
return output
model = Model()
# model = torch.nn.DataParallel(model, device_ids=device_ids)
model.cuda()
# 6. loss && optimizer
loss = torch.nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.001)
# 7. train
Linear_loss = []
for i in range(10):
# print("epoch: %d\n", i)
for data in linear_loader:
x, y = data['x'], data['y']
x = x.cuda()
y = y.cuda()
y_pred = model(x)
lloss = loss(y_pred, y)
optimizer.zero_grad()
lloss.backward()
for param in model.parameters(): # before optimize
print(param.item())
optimizer.step()
for param in model.parameters(): # after optimize
print(param.item())
Linear_loss.append(lloss.item())
print("Out--->input size:", x.size(), "output_size:", y_pred.size())
# 8. plot
loss_len = len(Linear_loss)
axis_x = range(loss_len)
plt.plot(axis_x, Linear_loss)
plt.show()