DFIG控制6-b：电流环分析
DFIG控制6-b：电流环分析。主要是PI控制器参数设计。
本文基于教程的第6部分。
DFIM Tutorial 6 - Dynamic Analysis of Current Loops in a Wind Turbine based on DFIG
电流环分析
对于网侧变换器GSC和转子侧变换器RSC，如果使用PI控制和正确的dq解耦，并且忽略变换器本身和控制延时（假设变换器能完美地提供所需的电压），那么电流环可以等效为一个二阶系统，也就可以用经典的控制理论方案设计PI控制器的参数。（具体可以再复习一下）
在GSC侧看起来更直观：
在RSC侧，原理相同，只是耦合项更多一些（下图是直接写出了类似上图右侧PI+一阶环节的闭环系统的表达式）：
所以GSC和RSC的电流环都可以等效为二阶系统，并且都与L和R有关。基于这一点可以使用类似的方法设计电流环PI控制器的参数。
PI参数设计
使用零极点配置的方法，选择PI控制器的参数。
典型二阶系统的传递函数：
ω n 2 s 2 + 2 ξ ω n s + ω n 2 \frac{\omega_n^2}{s^2+2\xi \omega_ns+\omega_n^2} s2+2ξωns+ωn2ωn2
GSC电流环的传递函数：
( k p g s + k i g ) / L s 2 + k p g + R L s + k i g L \frac{(k_{pg}s+k_{ig})/L}{s^2+\frac{k_{pg}+R}{L}s+\frac{k_{ig}}{L}} s2+Lkpg+Rs+Lkig(kpgs+kig)/L
令两者的分母相等，得到：
k p g + R L = 2 ξ ω n → k p g = 2 ξ ω n L − R k i g L = ω n 2 → k i g = ω n 2 L \begin{align*} \frac{k_{pg}+R}{L} &= 2\xi \omega_n \rightarrow k_{pg}=2\xi \omega_nL-R\\ \frac{k_{ig}}{L} &= \omega_n^2 \rightarrow k_{ig} = \omega_n^2 L \end{align*} Lkpg+RLkig=2ξωn→kpg=2ξωnL−R=ωn2→kig=ωn2L
然后就可以使用控制理论里学过的方法来选择 ξ \xi ξ和 ω n \omega_n ωn。例如，教程中是选择 ξ = 1 \xi=1 ξ=1，就只需要选择 ω n \omega_n ωn一个参数。
GSC电流环的传递函数为：
( 2 ω n − R / L ) s + ω n 2 ( s + ω n ) 2 \frac{(2\omega_n-R/L)s+\omega_n^2}{(s+\omega_n)^2} (s+ωn)2(2ωn−R/L)s+ωn2
用拉普拉斯反变换，可以写出时域的表达式。有空可以写一下，但是感觉表达式还是比较复杂，单从表达式看不出响应是怎么样的。
Rg = 20e-6; % Grid side filter's resisatance
Lg = 400e-6; % Grid side filter's inductance
wnig = 60*2*pi;
num_g = [2*wnig-Rg/Lg, wnig^2];
den_g = [1, 2*wnig, wnig^2];
wnig2 = 120*2*pi;
num_g2 = [2*wnig2-Rg/Lg, wnig2^2];
den_g2 = [1, 2*wnig2, wnig2^2];
step(num_g,den_g)
hold on
step(num_g2,den_g2)
figure(2)
bode(num_g,den_g)
hold on
bode(num_g2,den_g2)
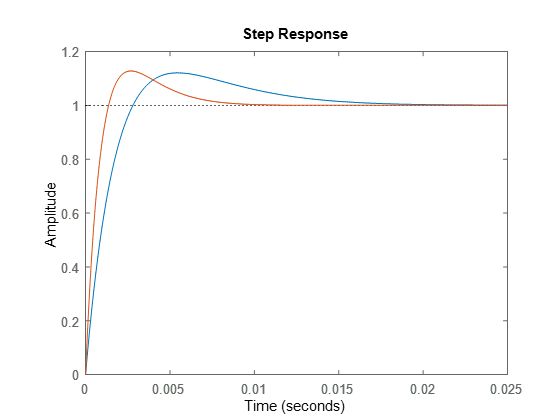
阶跃响和波特图。橙色对应wnig2 = 120*2*pi，蓝色对应wnig = 60*2*pi。 ω n \omega_n ωn越大，响应速度越快，闭环系统的带宽越高。
参数更新
教程中对RSC原来使用的参数做了更新，wni变为原来的1/5，教程给的理由是，RSC带宽不需要太高，修改后，RSC电流环带宽接近GSC的电流环带宽。同时，可以看到RSC和GSC的PI参数都是按照上文描述的方式选择的。不过对于wn的选择还是没有明确的说明。
% 电机的参数同前面几个教程。
% RSC current PI
tau_i = (sigma*Lr)/Rr;
wni = 100*(1/tau_i)/5; % 1/5 of that in Tutorial 1
kp_id = (2*wni*sigma*Lr)-Rr;
kp_iq = kp_id;
ki_id = (wni^2)*Lr*sigma;
ki_iq = ki_id;
% GSC current PI
tau_ig = Lg/Rg;
wnig = 60*2*pi;
kp_idg = (2*wnig*Lg)-Rg;
kp_iqg = kp_idg;
ki_idg = (wnig^2)*Lg;
ki_iqg = ki_idg;
% compare bode
num_r = [2*wni-Rr/(sigma*Lr), wni^2];
den_r = [1, 2*wni, wni^2];
num_g = [2*wnig-Rg/Lg, wnig^2];
den_g = [1, 2*wnig, wnig^2];
bode(num_g,den_g)
hold on
bode(num_r,den_r)
修改后的波特图对比：
仿真对比
主要是把4个电流的参考值输入给之前得到的二阶系统。电流环可被近似为这些二阶系统，所以，电流参考值相同的情况下，这些二阶系统的输出值应该接近仿真中RSC和GSC的电流值。仿真波形基本符合理论分析。
- 蓝色：电流参考值
- 红色：仿真波形
- 黄色：二阶系统模型
