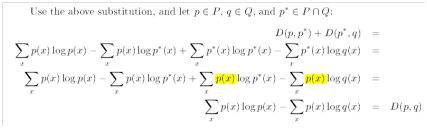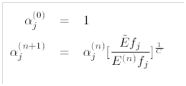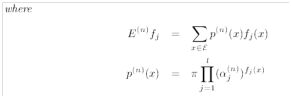最大熵原理与最大熵模型

最大熵原理非常简单，是一个关于最合理的概率分布的准则:

最合理的概率分布是包含已知信息，但不做任何未知假设，把未知事件当成等概率事件处理的概率分布.

利用最大熵原理求解最合理概率分布：

1. 把约束条件列出来（即把我们从sample中观察到一些现象用等式表达出来）
2. 把Entropy表达式写出来
3. 利用Lagrange Multiplier进行求解

最大熵模型:

我利用Adwait Ratnaparkhi 1997年的文章A Simple Introduction to Maximum Entropy Models for Natural Language Processing来进行阐述。

NLP中的许多问题其实都可以表示成分类问题，即在给定某种观察b的情况下，判断出目标是属于哪个类别a。对该分类问题的求解，我们可以进一步认为是要去估计一个联合概率分布

在不同的NLP任务中，所谓的观察b会有不同的呈现。比如，b有可能是目标前的一个词或一个字符；也可能是目标前后的各一个词；或者再包括上这些词的某些语法特征(如POS)等等。即便对某一个相同的NLP任务，不同的技术人员也会用到不同的b。比如，我们想要在字符层面上去做NER，我们可以用目标字符的前后2个字符作为观察，也可以用前后5个字符作为观察，去判断目标字符所对应的label。

一般说来class 的可能值不会太多，但是b里出现的字，词的可能值却有很多很多(dimensionality curse)，这导致即便在大规模的语料库里，我们都不可能找到足够多的(a,b)对，从而把对应所有(a,b)对的P(a,b)给准确地估计出来。

于是乎，我们现在的问题变成了如何利用在语料库中所得到的，稀疏的观察，即(a,b)对，去估计出一个最合理的联合概率分布。

最大熵原理指出，在所有能够与我们从稀疏的观察里总结出的“事实（或者说信息）”相匹配的概率分布中，拥有最大熵的那个概率分布式最合理可靠的。

那么现在，我们所要考虑的问题可以进一步被分拆为：

1. 如何在数学上去表达我们从稀疏的观察里总结出的“事实（或者说信息）”？如何从数学上去表达一个概率分布和这些“事实（或者说信息）”是相匹配的？
2. 当我们找到与“事实（或者说信息）”相匹配的概率分布的集合后，如何在这个集合中去找到具有最大熵的那个概率分布。

该问题其实就是一个典型的，寻找条件约束下最优值的问题。

如何在数学上去表达我们从稀疏的观察里总结出的“事实（或者说信息）”？如何从数学上去表达一个概率分布和这些“事实（或者说信息）”是相匹配的？

1. 这两个问题是关联在一起的。
2. 假如我们在语料库里发现，当b中存在某种特征时，a等于某个值的概率很高或很低；我们就可以定义一个二值函数，然后利用

来表达概率p和该发现是想匹配的。

我们在语料库里能够找到k种发现，就定义k种二值函数和匹配等式。这些匹配等式就是优化问题里的约束条件。

有了匹配等式后，最大熵原理给出的优化问题为

到此，我们已经把最大熵模型背后的逻辑讲清楚了。下面继续讲述优化问题的理论求解过程，就是解释为啥最大熵模型的解是以这种形态出现。

这里有几个定义需要先了解清楚:

概率分布集合P：

概率分布集合Q： ，这里是一个归一化参数。这个Q就是一个exponential family prob. functions set.

KL Divergence: 

任意两个概率分布函数p和q之间的KL Divergence都是非负的；如果有，那一定有。

我在这里就不去证明这个Lemma了，它的证明比较明显。

假定，而，那么 【和勾股定律类似！】

这个Lemma的证明如下，也是比较简单明了。

为了证明最大熵模型的解是以这种形态出现的，我们首先需要假设概率分布函数集合，因为如果P为空，整个任务就没有意义了。

其次，肯定是不为空的，因为至少uniform dist.就是该概率分布函数集合中的一个元素。

然后，我们需要证明。这个的证明在“Generalized Iterative Scaling for Log-Linear Models”里有。它的基本原理是说GIS算法产生的概率分布函数序列，会收敛到一个P里面的概率分布函数；同时由于GIS算法产生的概率分布函数序列都是Q里的函数，所以。

证明：如果，那么

的解就是

证明过程如下，非常清晰；利用了uniform distribution，同时也证明了的唯一性。

下面来讲讲最大熵和最大log likelihood之间的关系

首先定义

如果我们给定一个概率分布函数p，然后利用语料库来计算log likelihood，那么L(p)和log likelihood是成正比的。

如果存在一个，那么exponential family里的概率分布函数中对应最大log likelihood的概率分布函数就是

的解就是

Duality: P里对应最大熵的概率分布函数 = Q里对应最大log likelihood的概率分布函数

然后来讲讲Generalized Iterative Scaling （GIS）算法：

具体迭代过程如下

GIS算法里需要计算和

相对而言好计算：计算量不大。

因为b值的可能性很多，的计算量就可能很大：

为了降低计算量，我们采用一个近似方法。这样就避免了去计算所有可能的b值，而N（语料库的大小）不会太大，a值的可能性一般都不多。

 

后记：这篇文章清晰地阐述了最大熵模型的推导过程，以及最后的解为何是以exponential family的形式存在。在得出这个结论后，我们就能够得出条件概率。这也是网上大部分博客所提到的形式。只是我个人感觉直接利用拉格朗日方法来证明条件概率是以这种形式存在好像不够严谨，而这篇文章讲述了最大熵模型最初的推导过程，所有数学方法还是要严谨得多。