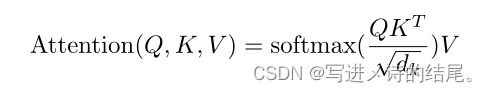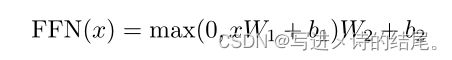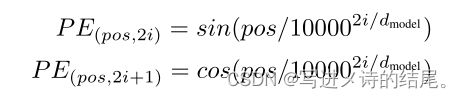Attention Is All You Need（Transformer，NIPS2017）

摘要

当前主流的序列转录模型，主要依赖较为复杂的循环或卷积神经网络，此类神经网络一般包括编码器（Encoder）和解码器（Decoder）结构。在性能最好的模型之中，也会在编码器和解码器之间使用注意力机制。

本文提出了一种新的简单的架构（Transformer），该架构完全基于注意力机制，而不涉及循环或卷积神经网络。在两个机器翻译任务上的实验表明，Transformer具有更佳的性能，更好的并行度，更少的训练时间。模型在WMT2014英译德翻译任务上获得了28.4%的BLEU成绩，比现有的最好成绩高2%以上。

序列转录模型：给定一个序列，生成另一个序列，比如机器翻译。
BLEU Score：机器翻译里常用的一个衡量标准。

（这篇文章一开始是针对机器翻译这个小任务来写的，但是随着BERT、GPT等把这个架构用在更多的语言处理任务上，整个工作就出圈了。最近还用在了图像和视频上，几乎什么东西都能用。）

引言

RNN、LSTM、GRU是用于解决序列建模和转录问题（如语言建模和机器翻译）的主流方法。这里有两个比较主流的模型：

• 一个叫做语言模型
• 另一个是当输出结构化信息比较多的时候会使用的编码器和解码器结构

在RNN中给定一个序列，它的计算方式是沿着这个序列从左到右一步一步往前做。假设序列是一个句子的话，操作对象就是一个一个的词，对第$t$个词会计算出一个输出叫做$h_t$（也叫做它的隐藏状态），$h_t$是由前面一个词的隐藏状态$h_{t-1}$和当前第$t$个词本身决定的，这样就可以把前面学到的历史信息通过$h_{t-1}$放到当下，然后和当前的词做一些计算，而后得到输出。

RNN处理时序信息存在的问题：

• 它是一个一步一步计算（时序）的过程，难以并行化处理，使得计算效率较差
• 历史信息一步一步往后传递，如果时序较长的话，那么早期的时序信息在后面可能要被丢弃。如果不想丢弃，就需要较大的$h_t$，每一步都得把它存下来，这会导致较大的内存开销

在这篇文章之前，注意力机制（Attention）已经成功用在了编码器和解码器之中，主要用于如何将编码器的东西有效地传递给解码器，常与RNN结合使用。

本文提出来的Transformer是一个新的模型，不再使用循环神经网络，而是仅使用注意力机制。该模型并行度较高，能够在较短时间内做到比之前更好的结果。

相关工作

卷积网络在做计算的时候，每次看的到是一个比较小的窗口，如果两个像素相隔比较远的话，需要用很多层卷积堆积起来，才能够把这两个隔得比较远的像素融合起来。但如果是使用Transformer里面的注意力机制的话，每一次都能够看到所有的像素，使用一层就能看到整个序列。

卷积的好处是可以做多个输出通道，一个输出通道可以认为是一个不一样的识别模式。作者也想要实现这种效果，所以提出了一个Multi-headed attention（多头注意力机制），用于模拟卷积神经网络中多输出通道的一个效果。

模型架构

序列模型中，比较好的是编码器和解码器结构。

编码器： 对于一个长为$n$的$(x_1,...,x_n)$输入序列，编码器会把它映射成一个长也为$n$的$(z_1,...,z_n)$向量表示，并将其作为输出序列。换句话说，编码器能够把原始输入变成机器学习可以理解的一系列向量。

解码器： 拿到编码器的输出序列，解码器会根据它来生成一个长为$m$的$(y_1,...,y_m)$序列，这里$n$和$m$可以相同，也可以不同。解码器和编码器最大的不同之处在于，在解码器中，词是一个一个生成的（对于编码器来说，可能一次性就能看全整个句子，而在解码的时候只能一个一个的生成），在过去时刻的输出也会作为当前时刻的输入，即自回归（auto-regressive）。

Transformer使用了编码器和解码器结构，具体来讲它是将self-attention、point-wise和fully connected layers一个一个堆在一起。

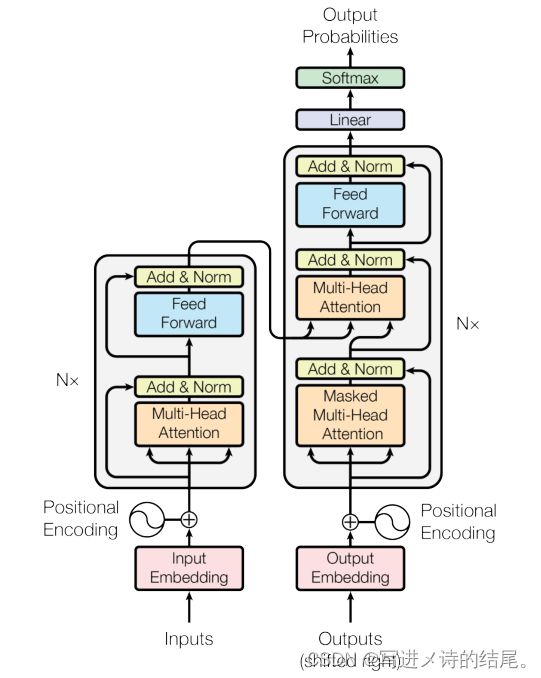
上图是Transformer的模型架构，也是编码器和解码器结构。左半边是编码器，右半边是解码器。左下角的Inputs是编码器的输入，如果是中文翻英文的话，输入就是中文的句子。右下角的Outputs是解码器的输入，解码器在做预测的时候是没有输入的，实际上这个输入是指解码器将之前时刻的一些输出作为输入（shifted right就是一个一个往右移）。Input Embedding表示嵌入层，进来的是一个一个的词，需要将它们表示成向量。Positional Encoding。Multi-Head Attention、Feed Forward、Add & Norm组合起来成为一个Transformer Block，类似于残差网络的残差块。N代表层数，由多个Transformer Block堆叠而成。编码器的输出会作为解码器的输入，解码器和编码器有点像，但是多了Masked Multi-Head Attention。编码器和解码器都可以认为是由几个部分组成的块重复N次。上图所示的确是一个标准的编码器和解码器结构，只是说中间的每一块有所不同，还有就是编码器和解码器之间的连接有所不同。

Transformer编码器： 该编码器由6个（N=6）完全一样的层组成。

• 每一个Layer中会有两个Sublayer
• 第一个Sublayer叫做Multi-Head Self-Attention
• 第二个Sublayer是一个simple position-wise fully connected feed-forward network，说白了就是一个MLP
• 对于每一个子层采用了一个残差连接，而后再使用Layer Normalization
• 经过Enbedding和Positional Encoding得到的x输入进来后会进入子层
• 因为是残差连接，所以经过子层得到的Sublayer(x)会跟x加在一起，再送入LayerNorm，可以写成LayerNorm(x+Sublayer(x))
• 残差连接需要x和Sublayer(x)的维度一样，如果不一样的话，就需要做投影。为了简单起见，把维度固定为512（固定表示长度的模型相对来说较为简单，调参的话只需调一个参数就行，就是模型的输出维度；另外一个参数就是重复的块N）

考虑一个最简单的二维输入情况，在这种情况下输入为一个矩阵，每一行是一个样本，每一列是一个特征。
BatchNorm所干的事情就是每一次在一个小mini-batch里，将每一列（若干样本的特征）数据的均值变成0，方差变成1。在训练的时候是在每一个小批量里面计算均值跟方差；对于预测，训练时会把所有数据扫一遍，然后计算全局的均值和方差，并将它们保存，以便在预测的时候再使用。BatchNorm会学习缩放因子和偏移因子两个参数，使得特征向量可以变成均值和方差为任意某个值的东西，增强表征能力。
LayerNorm和BatchNorm在很多时候几乎是一样的。对于一个同样的二维输入来说，LayerNorm是对每个样本做归一化，而不是多个样本。BatchNorm是将每个列（多个样本的同一通道特征）的均值变为0，方差变为1；LayerNorm是将每个行（一个样本的所有通道特征）的均值变为0，方差变为1。因此，LayerNorm可以认为是把整个数据转置一下放到BatchNorm中处理，然后出来的结果再转置回去。

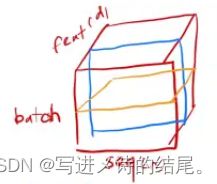
在Transformer或者正常的RNN中，输入是一个三维的东西，x轴表示序列（sequence），y轴表示特征向量（feature），z轴表示样本数量（batch）。可以想象成一个样本由一个句子序列组成，一个句子有多个词，每个词能映射成一个特征向量，然后多个样本构成一个矩形体，如下图所示。

如果用BatchNorm的话，每次对多个样本的同一位置特征进行处理，如上图中的蓝色正方形所示。相当于把这一块切下来拉成一个向量，然后进行均值和方差的计算。
如果用LayerNorm的话，每次对一个样本的所有位置特征进行处理，如上图中的黄色正方形所示。

切法不一样会带来不同的效果，为什么LayerNorm用的多一点？

• 在时序序列模型中，每个样本的长度可能不一样，没有东西的地方一般会填充零，如下面所示。主要问题在于均值和方差的计算上面，对于BatchNorm来说，会对下图中切出来的蓝色梯形部分进行均值和方差的计算（只有这部分是有效值，其余地方补零，并无多大作用），如果样本长度的变化较大，那么每次做小批量的时候，算出来的均值和方差的抖动相对来说是较大的

• 另外，在做预测的时候要把全局的均值和方差记录下来，如果这个均值和方差碰到一个新的特别长的预测样本，在训练时没见过这种长度，那么预测的效果可能就没那么好了
• 相反，LayerNorm相对来说没有太多的问题，因为它是按照每个样本来进行均值和方差的计算，同时也不需要记录全局的均值和方差，相对来讲更稳定一些

Transformer解码器： 解码器跟编码器很像，也是由6个（N=6）一样的层组成，每个层里也有Multi-Head Attention和Feed Forward两个子层。
与编码器不同的是，解码器中用了第三个子层Masked Multi-Head Attention，它同样是多头的注意力机制，也用了残差连接和LayerNorm。

解码器中做的是自回归，即当前时刻的输入来自前面一些时刻的输出，意味着在做预测的时候只能看到前面时刻的输出，而不能看到后面时刻的输出。
在注意力机制中，每一次都能够看到完整的输入，但是在解码的时候要避免看到完整的输入。也就是说在解码器训练的时候，预测第$t$个时刻的输出，不应该看到$t$时刻以后的那些输入。具体做法是增加一个带掩码的多头注意力机制，这个Masked的作用是保证输入进来的时候，$t$时刻只会看到之前的输出，而不会看到之后的输入，从而保证训练和测试时候的行为是一致的。

注意力机制（Attention）： 注意力函数可以被描述为将一个Query和一组Key-Value对映射成输出，其中Query、Keys、Values和输出都是向量。输出是Values的加权和，因此输出的维度和Value的维度是一样的。分配给每个Value的权重都是通过Query与相应Key的相似度函数计算得到的（compatibility function，不同的注意力机制有不同的算法，不同的相似度函数导致不一样的注意力版本）。

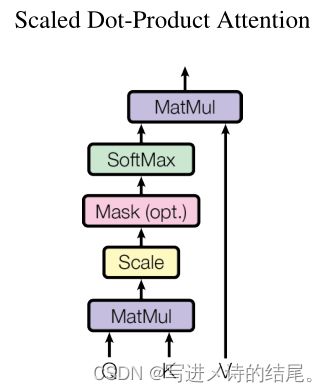
Scaled Dot-Product Attention： 如上图所示。

• 输入由Querys和Keys组成，它们的维度都是$d_k$（维度可以不一样，不一样的话有别的计算方法）

• Values的维度为$d_v$（输出的维度也应该是$d_v$）

• 具体计算，一个query向量和所有的key向量做内积，然后除以$\sqrt{d_k}$（$d_k$为向量的长度），而后通过Softmax函数得到所有value的权重（query向量和key向量的内积可以看作是相似度计算，内积越大，就表示这两个向量的相似度越高；如果内积为零，即正交，则表示这两个向量没有相似度。使用Softmax得到的权重具有非负、和为1的特性，这对于权重来说比较好），最后将这些权重作用在values上，进行加权和计算就能得到输出

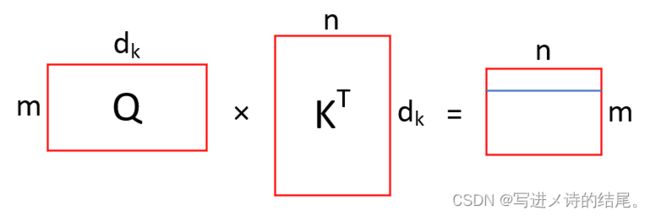
• 在实际操作中，不会一个一个的做运算，而是将一组query整合成一个矩阵Q，query的个数与key-value对的个数可能不一样，但query向量的长度与key向量的长度一定是一样的，这样才能进行内积运算

  

• 给定Q和K两个矩阵，通过矩阵相乘就会得到一个$m\times n$的矩阵，如下图所示，它的每一行（如图中蓝色线条所示）就是一个query向量和所有key向量的内积值。得到的矩阵会除以$\sqrt{d_k}$，再送入Softmax函数做概率计算（对每一行做Softmax，行与行之间是独立的），这样就能得到权重。权重矩阵再乘V（V是一个n行$d_v$列的矩阵，每一行表示一个value向量），得到一个$m\times d_v$的矩阵，这个矩阵的每一行就是所需要的输出。

  

• 对于m个query和n个key-value对，整个计算只需用到两次矩阵乘法，key和value在实际中对应的就是序列，这样就等价于是在并行地计算里面的每个元素（矩阵乘法便于并行）

一般有两种比较常见的注意力机制：

• 加性注意力机制（additive attention），可以处理query和key不等长的情况
• 乘性/点积注意力机制（multiplicative attention/dot-product attention），文中所用的就是点积注意力机制，唯一的区别就是文中的点积注意力多除以了一个$\sqrt{d_k}$，这个$\sqrt{d_k}$就是命名中提到的Scaled
• 这两种注意力机制其实都差不多，文章之所以选用点积注意力机制，是因为实现起来比较简单，两次矩阵相乘就能得到结果，而且效果比较好

这里为什么要除以$\sqrt{d_k}$：

• 当$d_k$不是很大的时候除不除都没关系。但是当$d_k$比较大的时候，也就是两个向量长度比较长的时候，做点积得到的值可能比较大也可能比较小
• 当值比较大的时候，向量之间相对的差距就会变大，导致内积值最大的那个值进行Softmax操作后就会更接近1，剩下的值就会更靠近0，值就会向两极分化。当出现这种情况后，在计算梯度的时候，梯度会比较小，就会跑不动（Softmax最后的结果是希望预测值置信的地方尽量靠近1，不置信的地方尽量靠近0，这样就差不多收敛了）
• 在Transformer里面一般用的$d_k$比较大（512），所以除以$d_k$是一个不错的选择

在Scaled Dot-Product Attention中，Mask主要是为了避免在第$t$时刻的时候看到以后时刻的东西。具体来说，假设query和key是等长的，长度都为n，而且在时间上能对应起来，对第$t$时刻的$q_t$做计算的时候，应该只是看到$k_1$到$k_{t-1}$，而不应该看到$k_t$和它之后的东西，因为$k_t$在当前时刻还没有。

但是在做注意力机制的时候，会发现其实$q_t$在跟矩阵K里全部的东西做运算，从$k_1$一直算到$k_n$，只要保证在计算权重的时候，不要用到后面的东西就可以了。

Mask的具体操作就是，对于$q_t$和$k_t$之后的用于计算的那些值，把它们替换成非常大的负数，这些大的负数在进入Softmax做指数运算后就会变成0，因而经过Softmax处理后出来的对应权重都会变成0，而$k_t$之前所对应的值都会有权重。

这样在计算输出的时候就只用到了V对应的$v_1$到$v_{t-1}$的结果，而$v_t$后面的东西并没有用到。

所以Mask的效果是在训练的时候，让第$t$个时刻的query只看到对应的前面的那一些key-value对，使得在做预测的时候能够进行一一对应。

Multi-Head Attention： 与其做一次单个的注意力函数，不如把整个Q、K、V投影到一个低维，投影h次，然后做h次的注意力函数，再将每一个函数结果并在一起，再投影回来得到最终的输出，如下图所示。

原始的values（V）、keys（K）、querys（Q）进入一个线性层（线性层将其投影到比较低的维度，投影h次），然后再做一个scaled dot-product attention，做h次，得到h个输出，再把这些输出向量全部合并到一起，最后做一次线性的投影，然后回到Multi-head attetion。

为什么要做多头注意力机制：

• dot-product的注意力机制中没有什么可学习的参数，具体函数就是内积。有时候为了识别不一样的模式，希望有一些不一样的计算像素的办法

• 如果是用加性注意力机制的话，里面其实是有一个权重可以学习的。但本文使用的是内积，它的做法是先投影到低维，这个投影的w是可以学的，也就是说，有h次机会希望可以学到不一样的投影方法，使得再投影进去的度量空间中能够匹配不同模式所需要的相似函数，最后把所得到的东西再做一次投影（这里有点像在卷积神经网络里面有多个输出通道的感觉）

• 具体的计算（公式如下图），在Multi-head的情况下，还是以前的Q、K、V，但是输出已经是不同头的输出做Contact运算再投影到一个$W^O$里面。对每一个头，就是把Q、K、V通过不同的可以学习的$W^Q$、$W^K$、$W^V$投影到$d_v$上面，再做注意力函数，然后再出来就可以了

• 虽然公式中看起来有很多小矩阵的乘法，实际上在实现的时候也可以仅通过一次的矩阵相乘来实现

在本文中，h是等于8的，也就是用了8个头。做注意力机制的时候，因为有残差连接的存在，使得输入和输出的维度是一样的。所以在投影的时候，投影的维度就是输出的维度除以h（输出维度是512，除以8之后，每一次把它投影到64维的维度，然后在这个维度上面计算注意力函数，最后再投影回来）。

Transformer通过三种方式来使用多头注意力机制，分别就是模型结构中的三个注意力层：

• 第一个注意力层，对于编码器的输入，假设句子长度是n的话，它的输入就是n个长为d的向量，每一个输入的词对应的就是一个长为d的向量，一共有n个词。
  编码器中的多头注意力层有三个输入，分别表示key、value、query，图中一根线复制成三根线，表示的是同样的东西，这个东西既作为key，也作为value，同时也作为query，这就叫自注意力机制。换句话说，key、value、query其实就是一个东西，就是它自己本身。
  假设不考虑多头和有投影的情况，输出其实是输入的加权和，权重来自于自己本身跟各个向量之间的相似度。如果有多头的话，因为有投影，会学习出h个不一样的距离空间出来，使得出来的东西会有点不一样
• 第二个注意力层，就是解码器中的Masked Multi-Head Attention。解码器也是一样的，也是同一个东西复制了三次，只是长度可能变成了m，所以它跟编码器中的一样也是自注意力，唯一不同的是里面有一个Mask（Mask的作用：在解码器计算query对应的输出的时候，不应该看到第$t$时刻后面的东西，意味着后面的东西要设为0）
• 第三个注意力层，就是解码器中的Multi-Head Attention。它不再是自注意力了，它的key和value来自编码器的输出，query来自解码器的上一个attention。编码器最后一层的输出就是n个长为d的向量，解码器的Masked Multi-Head Attention的输出就是m个长为d的向量。编码器的输出作为key和value传入到这个注意力层，解码器的上一层输出作为query传入到这个注意力层，这意味着query要计算出一个输出，这个输出是来自于value的一个加权和（来自于编码器的输出的加权和，权重的粗细程度取决于query与编码器输出的相似度，如果相似度比较高的话，权重就会大一点，如果相似度比较低的话，权重就会小一点）。这个注意力层中所要做的其实就是把编码器里面的输出根据需要有效地截取出来。

注意力机制如何在编码器和解码器之间传递信息的时候起作用：解码器根据当前的输入向量在编码器的输出里挑选感兴趣的东西，也就是去注意感兴趣的东西，那些不那么感兴趣的东西就可以忽略掉。

Position-wise Feed-Forward Networks： 其实就是一个fully connected feed-forward network，就是一个MLP，但是不同之处在于它是applied to each position seperately and identically（就是把同一个MLP对每个词作用一次，即position-wise，说白了就是MLP只是作用在最后一个维度）

• position：输入序列中有很多个词，每一个词就是一个点，这些点就是position

• 具体公式如下图所示，$x{W}_1+b_1$就是一个线性层，$max$就是ReLU激活层，最后再有一个线性层

  

• 在注意力层的输入（每一个query对应的输出）的长为512，$x$就是一个512的向量，$W_1$会把512投影成2048（等价于将它的维度扩大了4倍），因为有残差连接，所以还需要投影回去，因此$W_2$又把2048投影回512

• 这其实就是一个单隐藏层的MLP，中间的隐藏层将输入扩大4倍，最后输出的时候又回到输入的大小（如果用Pytorch来实现的话其实就是把两个线性层放在一起，而不需要改任何参数，因为Pytorch在输入为3维的时候，默认就是在最后一个维度做计算）

Embedding： 因为输入是一个一个的词（或者叫词源，token），需要将其映射成向量。Embedding的作用就是给任何一个词，学习一个长为d的向量来表示它（本文将d设置为512）

• 编码器的输入需要Embedding
• 解码器的输入也需要Embedding
• 在Softmax前面的线性层也需要Embedding

本文中这三个Embedding是一样的权重，这样的话训练起来会简单一点。另外还将权重乘了$\sqrt{d}$，维度一大的话，权重值就会变小，之后要加上positional encoding，它不会随着长度变长把它的long固定住，因此乘上了根号d之后，使得它们在scale方面差不多。

Positional Encoding： Attention没有时序信息，输出为value的加权和，权重是query和key之间的距离，和序列信息无关（也就是说给定一句话，把顺序任意打乱之后，经过Attetion出来的结果都是一样的，顺序会变，但是值不会变。这样是存在问题的，所以需要把时序信息加入进来）。

RNN是如何添加时序信息的？RNN将上一个时刻的输出作为下一个时刻的输入来传递历史信息。

Attention是在输入里面加入时序信息，将输入词所在的位置信息加入到输入里面（positional encoding），具体公式如下所示。

在计算机中，数字是用一定长度的向量来表示的。词在嵌入层会表示成一个长为d的向量，同样可以用一个长为d的向量来表示数字，也就是词的位置。这些数字的不同计算方法是使用周期不一样的sin和cos函数的值，所以说任何一个值可以用长为d的向量来表示，然后这个长为d的记录了时序信息的向量和嵌入层相加，就完成了将时序信息加进数据中的操作。因为是cos和sin的函数值是在+1和-1之间抖动的，所以乘了一个$\sqrt{d}$，使得每个数字也是差不多在±1的数值区间里面。

为什么要使用自注意力：

上表比较了四种不一样的层。第一个是自注意力层，第二个是循环层，第三个是卷积层，第四个是构造出来的受限的自注意力。第一列是计算复杂度，越低越好；第二列是顺序的计算，越少越好。指的是在算Layer的时候，下一步计算必须要等前面多少步计算完成，相当于是说非并行度；第三列说的是信息从一个数据点走到另一个数据点要走多远，越短越好。n是序列的长度，d是向量的长度。

整个自注意力就是几个矩阵做运算，其中一个矩阵运算是query矩阵（n×d）乘以key矩阵（也是n×d），两个矩阵相乘，算法复杂度就是n平方乘以d，别的矩阵运算复杂度也是一样的。因为只是牵涉到矩阵的运算，矩阵中可以认为并行度是比较高的，所以是o(1)。最大长度是说从一个点的信息想跳到另一个点要走多少步，在attention里面，一个query可以跟所有的key做运算，而且输出是所有value的加权和，所以query对任何一个很远的key-value对只要一次就能过来，所以长度是比较短的。

结论

Transformer是第一个完全基于注意力机制的序列转录模型，用Multi-headed self-attention取代了原编码器和解码器结构中最常用的循环层。对于机器翻译任务，Transformer的训练速度要比循环或卷积网络快很多，而且训练效果也要更好。作者对于这种完全基于注意力机制的模型感到很兴奋，想把它应用在文本以外的其他任务上，比如图像、音频、视频。