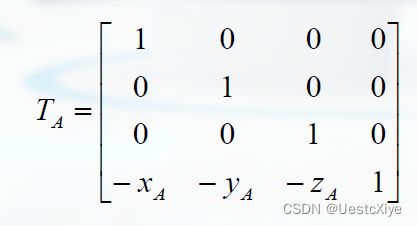计算机图形学 | 变换与观察
计算机图形学 | 变换与观察
- 计算机图形学 | 变换与观察
-
- 6.1 神奇的齐次坐标
-
- 回顾几何阶段
- 几何变换
-
- 平移
- 比例
- 旋转
- 对称
- 错切
- 齐次坐标的引入
-
- 齐次坐标的概念和相关问题
- 基于齐次坐标的变换
- 6.2 三维模型,动起来!
-
- 基本三维变换
-
- 平移
- 比例
- 旋转
- 对称
- 错切
- 整体比例变换
- 逆变换
-
- 平移的逆变换
- 比例变换的逆变换
- 旋转变换的逆变换
- 复合变换
-
- 相对于任一参考点的变换
- 绕任意轴的三维旋转变换
- 6.3 观察者也能动
-
- 绕任意轴的三维旋转变换
- 观察变换
- 模型变换与观察变换
华中科技大学《计算机图形学》课程
MOOC地址:计算机图形学(HUST)
计算机图形学 | 变换与观察
6.1 神奇的齐次坐标
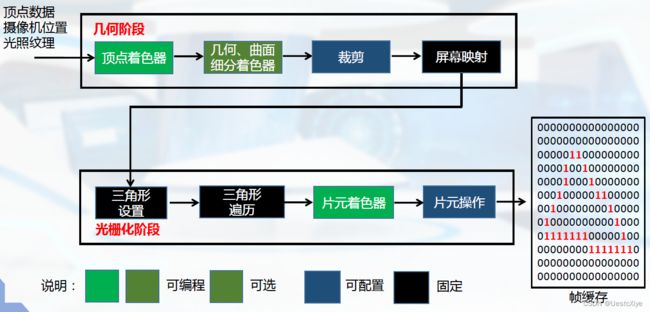
回顾几何阶段
整体流程:
这其中存在3种变换:
- 坐标系的变换
- 模型本身的运动
- 观察者的运动
几何变换
以上各种变换都可以通过以下变换的复合来计算:
- 平移
- 比例
- 旋转
- 对称
- 错切
图形的几何变换是指对图形的几何信息经过平移、比例、旋转等变换后产生新的图形。
下面以二维为例,讲解各个变换。
平移
指将p点沿直线路径从一个坐标位置移到另一个坐标位置的重定位过程,是一种不产生变形而移动物体的刚体变换(rigid-body transformation)。
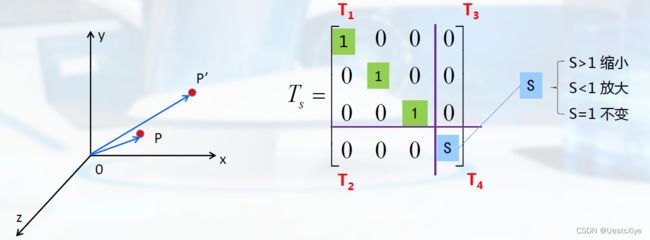
比例
对p点相对于坐标原点沿x方向放缩Sx倍,沿y方向放缩Sy倍。其中Sx和Sy称为比例系数。
旋转
将p点绕坐标原点转动θ角度(逆时针为正,顺时针为负)得到新的点p’的重定位过程。
对称
对称变换后的图形是原图形关于某一轴线或原点的镜像。
错切
也称为剪切、错位变换,用于产生弹性物体的变形处理。
总结:
齐次坐标的引入
齐次坐标的概念和相关问题
齐次坐标表示就是用n+1维向量表示一个n维向量。
以二维坐标系下点p(4,3)为例:齐次坐标表示为p(hx,hy,hz),具体可以为P(4,3,1), P(8,6,2)等等。
说明齐次坐标的不唯一性。
规范化齐次坐标表示就是h=1的齐次坐标表示。
规范化的方法:将每一维除以h。
以二维坐标系下点p(4,3)为例:齐次坐标表示为P(4,3,1), P(8,6,2)等等;其中,规范化齐次坐标表示P(4,3,1);
规范化:将P(8,6,2)规范化只需要对每一维除以h即可。即:P(8/2,6/2,2/2)得到P(4,3,1)。
基于齐次坐标的变换
全部统一为矩阵运算:
其中:
T1是对图形进行比例、旋转、对称、错切等变换;
T2是对图形进行平秱变换;
T3是对图形作投影变换;
T4则可以对图形作整体比例变换。
整体比例变换:
如果有多个点?如果变换多次呢?
6.2 三维模型,动起来!
基本三维变换
基本的三维变换包括:
- 平移
- 比例
- 旋转
- 对称
- 错切
三维坐标(x,y,z)的齐次坐标表示(hx,hy,hz,h)。
以维坐标系下点p(4,3,2)为例:齐次坐标表示具体可以为P(4,3,2,1), P(8,6,4,2)等,规范化齐次坐标表示为P(4,3,2,1)。
基于三维齐次坐标的变换:
T1:3×3阶子矩阵,作用是对点进行比例、对称、旋转、错切变换
T2:1×3阶子矩阵,作用是对点进行平移变换
T3:3×1阶子矩阵,作用是进行投影变换
T4:1×1阶子矩阵,作用是进行整体比例变换
平移
指将p点沿直线路径从一个坐标位置移到另一个坐标位置的重定位过程,是一种不产生变形而移动物体的刚体变换(rigid-body transformation)。
比例
对p点相对于坐标原点沿x方向放缩Sx倍,沿y方向放缩Sy倍,沿z方向放缩Sz倍。其中Sx、Sy和Sz称为比例系数。
旋转
将p点绕坐标轴转动θ角度得到新的点p’的重定位过程。
正方向如何确定?
按右手定则,规定逆时针为正,顺时针为负。
对称
对称变换后的图形是原图形关于某一轴线、某一坐标平面或原点的镜像。
关于坐标平面:
关于坐标轴:
错切
也称为剪切、错位变换,用于产生弹性物体的变形处理。
假设有一个x方向上的错切则:x’=x+dy+gz。
整体比例变换
整体比例变换:对p点相对于坐标原点沿x方向放缩S倍。
逆变换
所谓逆变换即是与上述变换过程的相反的变换。
平移的逆变换
平移的逆变换就是反向平移,将平移后的点移回到原处。
其变换矩阵为:
比例变换的逆变换
比例变换的逆变换就是将比例因子取为倒数。
其变换矩阵为:
旋转变换的逆变换
旋转变换的逆变换就是反向旋转,也就是将旋转角度由θ改为- θ。
其变换矩阵为:
复合变换
三维复合变换是指图形作一次以上的变换,变换结果是每次变换矩阵相乘。
相对于任一参考点的变换
相对于参考点F(xf,yf,zf)作比例、旋转、错切等变换的过程分为以下三步:
- 将参考点F移至坐标原点
- 针对原点进行二维几何变换
- 进行反平移
绕任意轴的三维旋转变换
答案将在下一节给出。
6.3 观察者也能动
绕任意轴的三维旋转变换
假设已知空间有任意轴AB,A点的坐标为A(xA,yA,zA),AB的方向数为(a,b,c)。
现有空间一点p(x, y, z) ,绕AB轴逆时针旋转θ角后成为p’ (x’, y’, z’ ) ,若旋转变换矩阵为TRAB。
则:[x’ y’ z’ 1] = [x y z 1] · TRAB
问题:如何求出TRAB?
步骤:
- 把A点移动到坐标原点
- 把AB轴绕到某个坐标轴上
- 旋转
- 求1、2变换的逆变换,回到AB原来的位置
第一步:把A点移动到坐标原点
第二步:把AB轴绕到某个坐标轴上
绕x轴正转α角,将O’B’转动到XOZ平面上
绕y轴反转β角,将O’B’转动到z轴上
第三步:旋转
此时,AB轴与z‘轴重合,此时绕AB轴的旋转转换为绕z轴的旋转。
绕z轴旋转θ角的旋转变换矩阵为:
第四步:求1、2变换的逆变换,回到AB原来的位置
也就是求 TtA ,TRx ,TRy 的逆变换。
总结:
观察变换
观察变换:从世界坐标系到观察坐标系的转换。
观察坐标系:
坐标原点:观察者所在的位置。
其中:
zv:视点和观察物体上焦点的连线
yv:向上的方向
xv:按照右手定则确定的方向
实际上求什么?
求世界坐标系中点Q(x,y,z)在观察坐标系中的坐标值。
观察变换的实现:
模型变换与观察变换
观察变换的应用:场景漫游
模型变换不观察变换具有对偶性。但是由于场景中只有部分物体运动,所以效果不同。