【Diffusion Model】Learning notes
来自 扩散模型 Diffusion Model 1-1 概述
扩散模型是什么？
本质是生成模型，拟合目标分布，然后生成很多数据符合这个分布
训练测试阶段？
和 GAN 相比优势是什么？
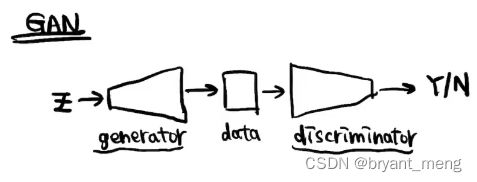
generator 和 discriminator 两者都得训练的比较均衡才能得到好的结果（稳定性），两者对抗，loss 并不能直观的反应训练过程
- 训练难度
- 训练稳定性
- loss 的复杂性
DDPM 的话，reverse 只是一个去噪模型，目标比较明确，易于训练
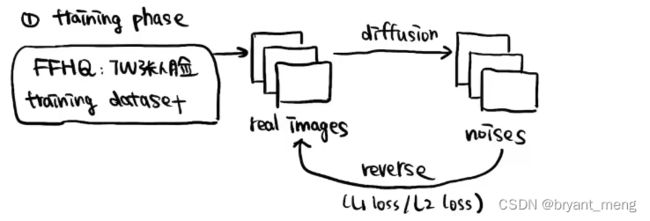
扩散阶段
Z t Z_t Zt 服从标准正态分布
β t \beta_t βt 加权系数，越来越大
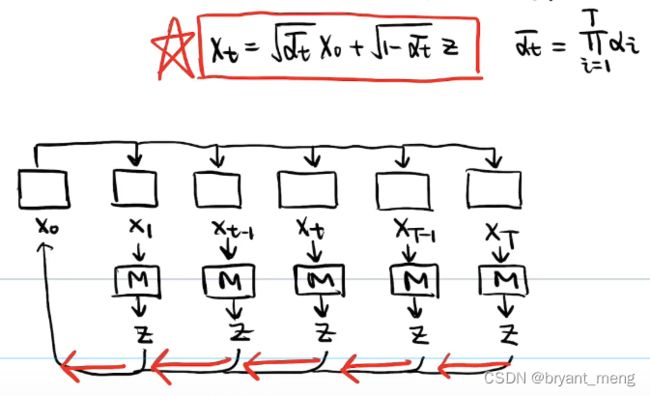
上图是从 X t X_t Xt 到 X t − 1 X_{t-1} Xt−1 的公式
每张图加噪 T 次太慢了
我们能否直接从 X 0 X_0 X0 直接推导到 X t X_t Xt 呢？
α t \alpha_t αt
X T ≈ Z X_T \approx Z XT≈Z 近似高斯噪声
reverse 的过程这里简单的进行了表示
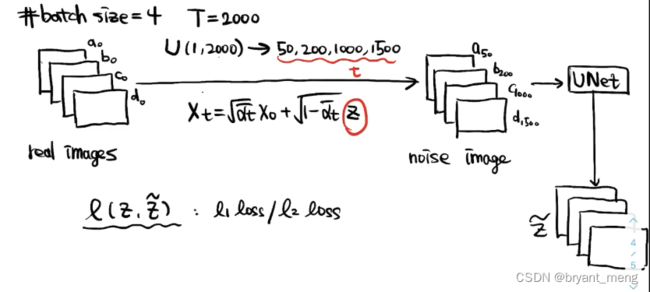
看看多 batch 的时候是怎么训练的
扩散过程
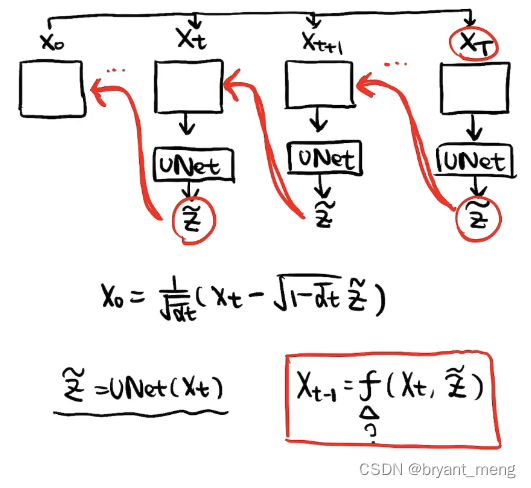
Z ~ = U N e t ( X t , t ) \widetilde{Z} = UNet(X_t, t) Z =UNet(Xt,t)
reverse 的形式是什么样子的呢？
也是一步步反推回来的
具体看看 reverse 的公式推导
也即，求条件概率 p ( X t − 1 ∣ X t ) p(X_{t-1}| X_t) p(Xt−1∣Xt)
注意上公式2中 p ( X t ) p(X_t) p(Xt) 表示 p ( X t ∣ X 0 ) p(X_t | X_0) p(Xt∣X0)， 公式3中 p ( X t − 1 ) p(X_{t-1}) p(Xt−1) 表示 p ( X t − 1 ∣ X 0 ) p(X_{t-1} | X_0) p(Xt−1∣X0)
正太分布这里忽略了 1 2 π ⋅ σ \frac{1}{ \sqrt{2 \pi} \cdot \sigma} 2π⋅σ1
把公式1/2/3代入公式4得到公式5
公式4的目的是求出 p ( X t − 1 ∣ X t ) p(X_{t-1} | X_t) p(Xt−1∣Xt)， X t − 1 X_{t-1} Xt−1 为变量，把公式5按二次式展开
已知： α t + β t = 1 \alpha_t + \beta_t = 1 αt+βt=1， α t ⋅ α t − 1 ‾ = α t ‾ \alpha_t \cdot \overline{\alpha_{t-1}} = \overline{\alpha_t} αt⋅αt−1=αt
方差
均值
得到了关于 X t X_t Xt 和 X 0 X_0 X0 的表达形式
我们要求的是条件概率 p ( X t − 1 ∣ X t ) p(X_{t-1}| X_t) p(Xt−1∣Xt)， X 0 X_0 X0 不知道的，所以要替换掉上式中的 X 0 X_0 X0
得到最终的均值结果，与 X t X_t Xt 和 z ~ \widetilde{z} z 有关
汇总一下：
这里 X t − t X_{t-t} Xt−t 的公式有误，应该为
z z z 服从标准的正态分布
X t − t X_{t-t} Xt−t 公式模拟分子的布朗运动， X t − 1 X_{t-1} Xt−1 中加式1 z ~ \widetilde{z} z 是确定项，加式2 z z z 是随机的正态分布
布朗运动和扩散现象的区别
注意红色字迹的三个基础公式
对应到论文中的公式
扩散阶段
reverse 阶段
注意到这里的 if t>1，最后一步，不需要加扰动噪声了
σ t \sigma_t σt 表示了扰动的系数，非确定性项
有可能 z z z 采样出来的全为0，这样 reverse 的过程变成了一个确定的过程
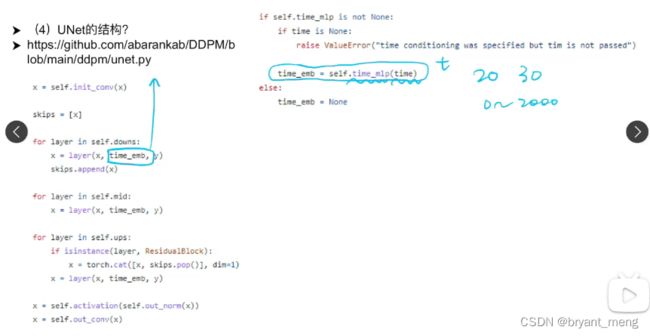
代码实现
α \alpha α 和 β \beta β 的获取
t t t 为 index
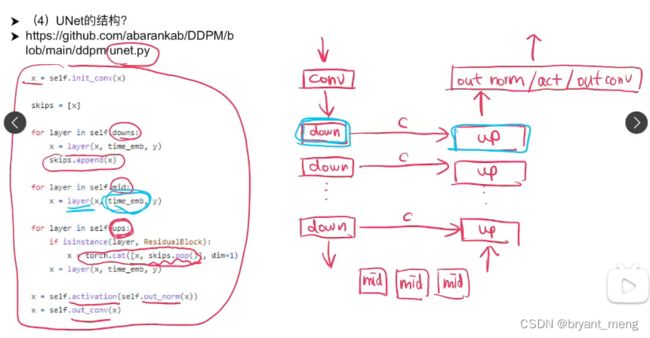
time embedding 操作，不同时间点做不同的去噪操作
Residual block
time embedding，类似于 transformer 的位置编码
