『数据结构』二叉搜索树

什么是二叉搜索树

---

二叉搜索树（Binary Search Tree），（又名：二叉查找树、二叉排序树）它或者是一棵空树。是一种特殊的二叉树，具有以下性质：

• 若它的左子树不为空，则左子树上所有节点的值都小于根结点的值。
• 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值。
• 它的左右子树也分别为二叉搜索树。

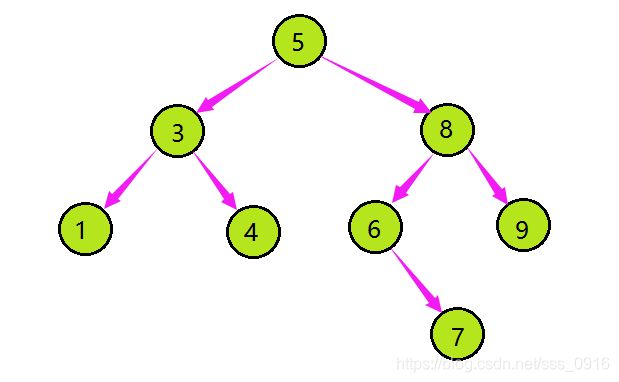
二叉搜索树原理：
二叉搜索树的查找过程和二叉树类似，通常采取二叉链作为二叉搜索树的存储结构。中序遍历二叉搜索树可以可到一个关键字的有序序列；一个无需序列可以通过构造一棵二叉搜索树变成一个有序序列，构造树的过程即为对无需序列进行排序的过程。每次插入的新节点都是二叉搜索树上新的叶子节点，在进行插入操作时，不必移动其他节点，只需要改动某个节点的指针，由空变为非空即可。二叉搜索树搜索、插入、删除的复杂度等于树高，O(log(n))。

二叉搜索树的操作

---

二叉搜索树的查找：

• 若根节点不为空：
  如果根节点key==查找的key，返回true；
  如果根节点key>查找的key，在其左子树查找；
  如果根节点key<查找的key，在其右子树查找；
• 若根节点为空，返回false；
  

二叉树的插入：
插入的过程如下：

1. 如果树为空，则直接插入，然后返回true。
   
2. 树不为空，按二叉搜索树的性质查找插入位置，插入新节点。
   

二叉搜索树的删除：
设待删除节点为cur，待删除节点的双亲节点为parent。分为下面三种情况：

• cur.left == null
  待删除节点是根节点，则root = cur.right;
  
  待删除节点是其双亲节点的左孩子，则parent.left = cur.right;
  
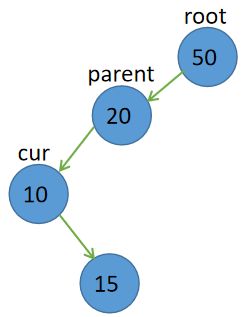
  待删除节点是其双亲节点的右孩子，则parent.right = cur.right;
  
• cur.right == null
  待删除节点是根节点，则root = cur.left;
  
  待删除节点是其双亲节点的左孩子，则parent.left = cur.left;
  
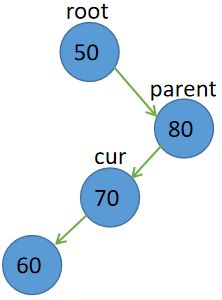
  待删除节点是其双亲节点的右孩子，则parent.right = cur.left;
  
• cur.left != null && cur.right != null
  需要使用替换法进行删除，在它的右子树中找到最左节点，将最左节点的值赋给待删除节点，然后删除替代节点。

二叉搜索树性能分析

---

插入和删除操作都必须先查找，查找效率代表了二叉搜索树中各个操作的性能。
对有n个结点的二叉搜索树，若每个元素查找的概率相等，则二叉搜索树平均查找长度是结点在二叉搜索树深度的函数，即结点越深，比较次数越多。
但对于同一个键值集合，如果各键值插入的次序不同，可能得到不同结构的二叉搜索树。

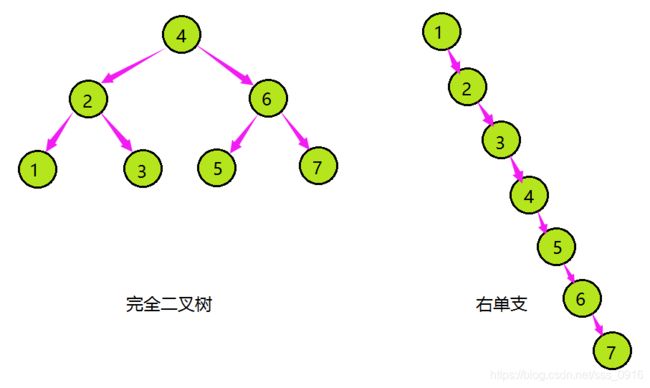
• 最优情况下，二叉搜索树为完全二叉树，平均比较次数为：log2(N)；
• 最差情况下，二叉搜索树退化为单支树，平均比较次数为：N/2；

如果退化成单支树，二叉搜索树的性能就失去了。这就是二叉搜索树的问题所在。有没有什么改进的方法呢？有，但是这里就不介绍了。可以提一下：AVL树。

模拟实现二叉搜索树

---

C++版

---

模拟实现中遇到的问题：

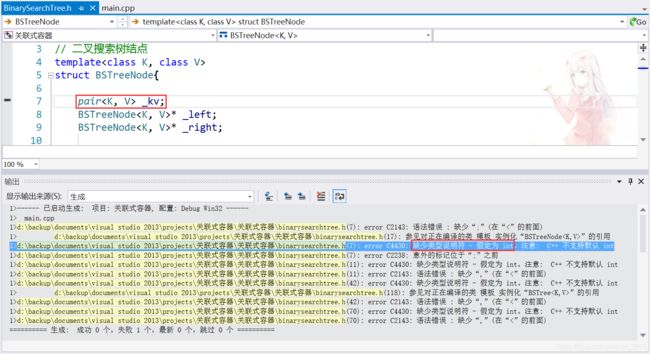
二叉搜索树结点中pair _kv;语句报错，缺少类型说明符。错误原因暂时不详。
解决方案如下：
将第3行和第4行交换一下，就可以了O(∩_∩)O哈哈~。


BinarySearchTree.h：

#pragma once

// 二叉搜索树结点
template<class K, class V>
struct BSTreeNode{

	pair<K, V> _kv;
	BSTreeNode<K, V>* _left;
	BSTreeNode<K, V>* _right;

	BSTreeNode(const pair<K, V>& kv)
		: _left(nullptr)
		, _right(nullptr)
		, _kv(kv)
	{}

};

// 二叉搜索树
template<class K, class V>
class BSTree{
	typedef BSTreeNode<K, V> Node;

public:
	BSTree()
		: _root(nullptr)
	{}

	~BSTree(){
		// 二叉搜索树的释放
		_release(_root);
	}

	// 二叉树的中序遍历
	void inorder(){
		_inorder(_root);

		cout << endl;
	}

	// 二叉搜索树的查找
	Node* find(const K& key){
		return _find(key);
	}

	// 二叉搜索树的插入
	bool insert(const pair<K, V>& kv){
		return _insert(kv);
	}

	// 二叉搜索树的删除
	bool remove(const K& key){
		return _remove(key);
	}

private:
	// 释放
	void _release(Node* root){
		// 该树非空
		if (root){
			// 保存左右孩子
			Node* left = root->_left;
			Node* right = root->_right;

			// 释放根
			delete root;

			// 左树非空，释放左树
			if (left){
				_release(left);
			}

			// 右树非空，释放右树
			if (right){
				_release(right);
			}
		}
	}

	// 中序遍历
	void _inorder(Node* root){
		// 递归出口
		if (root == nullptr){
			return;
		}

		_inorder(root->_left);
		cout << root->_kv.first << " ";
		_inorder(root->_right);
	}

	// 查找
	Node* _find(const K& key){
		Node* cur = _root;

		while (cur != nullptr){
			// 比根结点大，去右子树找
			if (key > cur->_kv.first){
				cur = cur->_right;
			}
			// 比根结点小，去左子树找
			else if (key < cur->_kv.first){
				cur = cur->_left;
			}
			// 相等
			else{
				break;
			}
		}

		return cur;
	}

	// 插入
	bool _insert(const pair<K, V>& kv){
		// 树为空
		if (_root == nullptr){
			_root = new Node(kv);

			return true;
		}
		// 树不为空
		else{
			Node* cur = _root;
			// 保存父节点
			Node* parent = nullptr;

			while (cur != nullptr){
				parent = cur;

				// 比根结点大，去右子树
				if (kv.first > cur->_kv.first){
					cur = cur->_right;
				}
				// 比根结点小，去左子树
				else if (kv.first < cur->_kv.first){
					cur = cur->_left;
				}
				// 和根结点一样，已存在，插入失败
				else{
					return false;
				}
			}

			// 新插入结点
			cur = new Node(kv);

			// 比双亲结点大，插入到右树
			if (kv.first > parent->_kv.first){
				parent->_right = cur;
			}
			// 比双亲结点小，插入到左树
			else{
				parent->_left = cur;
			}

			return true;
		}
	}

	// 删除
	bool _remove(const K& key){
		Node* cur = _root;
		// 保存父结点
		Node* parent = nullptr;

		while (cur != nullptr){
			// 比根结点大，右树找
			if (key > cur->_kv.first){
				parent = cur;
				cur = cur->_right;
			}
			// 比根结点小，左树找
			else if (key < cur->_kv.first){
				parent = cur;
				cur = cur->_left;
			}
			// 找到了
			else{
				// 该节点左树为空
				if (cur->_left == nullptr){
					// 该节点为根结点
					if (parent == nullptr){
						_root = cur->_right;
					}
					else{
						// 该节点在父结点的右树
						if (cur->_kv.first > parent->_kv.first){
							parent->_right = cur->_right;
						}
						// 该节点在父结点的左树
						else{
							parent->_left = cur->_right;
						}
					}
				}
				// 该节点右树为空
				else if (cur->_right == nullptr){
					// 该节点为根结点
					if (parent == nullptr){
						_root = cur->_left;
					}

					// 该节点在父结点的右树
					if (cur->_kv.first > parent->_kv.first){
						parent->_right = cur->_left;
					}
					// 该节点在父结点的右树
					else{
						parent->_left = cur->_right;
					}
				}
				// 该节点左右树都不为空
				else{
					// 右树中寻找替代结点
					Node* replace = cur->_right;
					// 保存替代结点的父结点
					Node* rparent = cur;

					// 寻找最左结点，即右树中的最小值
					while (replace->_left){
						rparent = replace;
						replace = replace->_left;
					}

					cur->_kv = replace->_kv;
					cur = replace;

					// 判断replace是否有左树
					// replace有左树
					if (rparent->_left == replace){
						// 将替代结点的右树连到替代结点的父结点的左树
						rparent->_left = replace->_right;
					}
					// replace没有左树
					else{
						// 将替代结点的右树连到替代结点的父结点的右树
						rparent->_right = replace->_right;
					}
				}

				// 删除替代结点
				delete cur;

				return true;
			}
		}
		return false;
	}

private:
	Node* _root;
};

Java版

---

public class BinarySearchTree<K extends Comparable<K>, V> {
    public static class TreeNode<K extends Comparable<K>, V> {
        public K key;
        public V value;

        public TreeNode<K, V> left = null;
        public TreeNode<K, V> right = null;

        public TreeNode(K key, V value) {
            this.key = key;
            this.value = value;
        }

        @Override
        public String toString() {
            return String.format("{%s, %s}", key, value);
        }
    }

    private TreeNode<K, V> root = null;

    // 查找
    public V get(K key) {
        TreeNode<K, V> curNode = this.root;

        while (curNode != null) {
            int flag = key.compareTo(curNode.key);
            if (flag > 0) {
                curNode = curNode.right;
            } else if (flag < 0) {
                curNode = curNode.left;
            } else {
                return curNode.value;
            }
        }
        return null;
    }

    // 插入
    public void put(K key, V value) {
        if (this.root == null) {
            this.root = new TreeNode<>(key, value);
            return;
        }

        TreeNode<K, V> parent = null;
        TreeNode<K, V> curNode = this.root;
        while (curNode != null) {
            parent = curNode;

            int flag = key.compareTo(curNode.key);
            if (flag > 0) {
                curNode = curNode.right;
            } else if (flag < 0) {
                curNode = curNode.left;
            } else {
                curNode.value = value;
                return;
            }
        }

        TreeNode<K, V> newNode = new TreeNode<>(key, value);
        int flag = key.compareTo(curNode.key);
        if (flag > 0) {
            parent.right = newNode;
        } else {
            parent.left = newNode;
        }
    }

    // 删除
    public V remove(K key) {
        TreeNode<K, V> parent = null;
        TreeNode<K, V> curNode = this.root;
        while (curNode != null) {
            int flag = key.compareTo(curNode.key);
            if (flag > 0) {
                parent = curNode;
                curNode = curNode.right;
            } else if (flag < 0) {
                parent = curNode;
                curNode = curNode.left;
            } else {
                V ret = curNode.value;

                if (curNode.left == null) {
                    if (curNode == this.root) {
                        this.root = curNode.right;
                        return ret;
                    }
                    if (curNode == parent.left) {
                        parent.left = curNode.right;
                        return ret;
                    }
                    if (curNode == parent.right) {
                        parent.right = curNode.right;
                        return ret;
                    }
                } else if (curNode.right == null) {
                    if (curNode == this.root) {
                        this.root = curNode.left;
                        return ret;
                    }
                    if (curNode == parent.left) {
                        parent.left = curNode.left;
                        return ret;
                    }
                    if (curNode == parent.right) {
                        parent.right = curNode.left;
                        return ret;
                    }
                } else {
                    TreeNode<K, V> replaceParent = curNode;
                    TreeNode<K, V> replaceNode = curNode.right;
                    while (replaceNode.left != null) {
                        replaceParent = replaceNode;
                        replaceNode = replaceNode.left;
                    }

                    curNode.key = replaceNode.key;
                    curNode.value = replaceNode.value;

                    if (replaceNode == replaceParent.left) {
                        replaceParent.left = null;
                    } else {
                        replaceParent.right = null;
                    }

                    return ret;
                }
            }
        }

        return null;
    }
}