(Deep Learning)交叉验证(Cross Validation)
交叉验证(Cross Validation)
交叉验证(Cross Validation)是一种评估模型泛化性能的统计学方法,它比单次划分训练集和测试集的方法更加稳定、全面。
交叉验证不但可以解决数据集中数据量不够大的问题,也可以解决模型参数调优的问题。
交叉验证主要有以下三种方式:
1.简单交叉验证(Simple Cross Validation)
其中,简单交叉验证将原始数据集随机划分为训练集(Train Set)和测试集(Test Set)两部分。
例如:将原始数据样本按照7:3的比例划分为两部分,其中70%的样本用于训练模型,30%的样本用于测试模型及参数。
缺点:
(1)数据样本仅被使用一次,没有得到充分的利用。
(2)在测试集上得到的最终评估指标可能与数据集的划分有很大的关系。
2.K折交叉验证(K-fold Cross Validation)
为了解决简单交叉验证的不足,提出了K折交叉验证。
K折交叉验证的流程为:
(1)首先将全部样本划分成K个大小相等的样本子集
(2)依次遍历这K个子集,每次把当前子集作为验证集,其余所有样本作为训练集,进行模型的训练和评估
(3)最后把K次评估指标的平均值作为最终的评估指标,在实际实验中,K通常取10
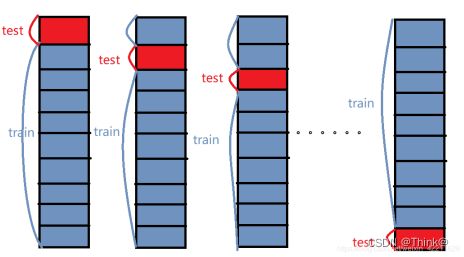
例如,当K取10时,K折交叉验证如下图所示:
(1)先将原始数据集分成10份,此时每一份中包含的数据样本数为D
(2)每次将其中的一份作为测试集,剩下的9份(即K-1份)作为训练集,此时训练集就变成了(K-1)*D
(3)最后计算K次求得的评价指标的平均值,作为该模型或者假设函数的真实性能
3.留一交叉验证(Leave-one-out Cross Validation)
留一交叉验证是K折交叉验证的特殊情况,当K等于样本数N时,对于这N个样本,每次选择N-1个样本来训练数据,留一个样本来验证模型预测的好坏。
留一交叉验证主要用于样本量非常少的情况,例如:对于普通适中问题,当N小于50时通常使用留一交叉验证。
交叉验证的方法在数据理解上较为简单,且具有说服性,但需要谨记的是,当样本总数过大时,使用留一法的时间开销极大。
以下内容转载自知乎:
一:交叉验证(Cross Validation)
在K折交叉验证之前最常用的验证方法是简单交叉验证,即把数据划分为训练集(Train Set)、验证集(Validation Set)和测试集(Test Set)。一般的划分比例为6:2:2。但如何合理的抽取样本就成为了使用交叉验证的难点,不同的抽取方式会导致截然不同的训练性能。同时由于验证集和测试集是不参与训练的,导致大量的数据无法应用于学习,所以显而易见的会导致训练的效果下降。
二:K折交叉验证
将训练集(Train Set)数据划分为K部分,利用其中的K-1份训练模型,剩余的1份作为测试,最后取平均测试误差做为泛化误差。这样做的好处是,训练集(Train Set)的所有样本在必然成为训练数据的同时也必然有机会成为1次测试集。因此,K折交叉验证可以更好的利用训练集(Train Set)数据。
在K折交叉验证中,K越大,被视为泛化误差的平均误差结果就越可靠,但K越大,进行K折交叉验证所花费的时间也是呈线性增长的。
三:存在的问题
以上所述均为书上的内容,但我发现这一步存在一个问题?即在进行K折之前是否需要划分训练集(Train Set)和测试集(Test Set)。
如果划分训练集(Train Set)和测试集(Test Set),(跑论文的实验)在利用公开数据集进行训练时,在相同网络相同数据集的情况下,你的结果可能比别人差(你只使用80%的数据进行训练,而不进行划分则可以使用所有的数据进行训练)。
如果划分测试集,在一些小规模的数据集中该怎么办?可能数据集本身就只有少量数据,此时分走20%用做测试,则用于训练的数据更加不够。
如果不划分测试集(Test Set),直接对所有数据进行K折,网络层数、学习率(Learning Rate)这些参数好定,但是学习轮次(Epoch)怎么决定,到什么程度停止学习。你不能选择测试集上效果最好的轮次,因为这会泄露一部分信息给模型。同时如果最后想要选出一个最佳的模型怎么办?
四:不同情况下给出的可行的——K折验证的方案
情况1:大数据规模
直接使用简单交叉验证(Simple Cross Validation),无需使用K折。因为数据规模较大时,即使以6:2:2的形式划分训练集(Train Set)-验证集(Validation Set)-测试集(Test Set)。其中60%的数据都足以代表所有数据的分布。
举个例子:现在我们需要通过统计的方法去计算投掷骰子时,每个点出现的概率。你现在做了100万次独立的实验,即使你只使用了其中的六十万次的结果也足以得到一个让人信服的概率,即每个点数出现的概率为六分之一。
情况2:中小规模的数据
1:公司使用的情况:首先划分训练集(Train Set)和测试集(Test Set)。在训练集上进行K折,K折中每1折在验证集中误差最小的模型(因为事先划分了训练集和测试集,书中所述的K折中的测试集我在这里称它为验证集(Validation Set))被放在测试集上进行测试,计算测试误差。最后模型的性能为每折中选中的模型在测试集上误差的平均。
(为什么说K折中每1折在验证集上误差最小的模型。因为在训练之前我们并不知道算法需要训练多少轮次才会达到最佳效果,所以我的想法是尽可能的让他多跑,然后在里面选在验证集上表现最佳的模型。再把选出来的模型丢到测试集上去测。)
对中小规模数据集、公司商用情况下流程的意识流示意图
ps:划分之后,会存在训练集数据不足的问题,但是在公司的项目中你必然要选出一个合适的模型进行部署,不先进行训练集和测试集的划分是选不出来合适的模型的!
2:论文实验的情况:如在论文实验中划分训练集(Train Set)和测试集(Test Set),则会存在说服力的问题。即:如何保证你选用的测试集不是经过你精心挑选的,十分容易判断的简单样例!所以,在不需要挑选出最佳模型而仅需评估方法效果的情况下,可以直接在所有的数据上进行K折。这样做的好处在于:你所使用的数据多了,模型的效果也更好,在测试集上的测试误差也会更加接近于泛化误差。
但是这样做会存在一个训练的迭代次数的问题,即:你将在何时停止你学习的过程。
在仅划分训练集(Train Set)和测试集(Test Set)的情况下,你只有两种可行的方法:
(1)选测试集上效果最好的,这就存在将测试集数据分布泄露给训练集的问题。
(2)定死迭代次数,这存在怎么选迭代次数的问题。
因此给出我的方法:在整个数据集上进行K折。在划分的训练集(Train Set)中,抽取一小部分比如5%做为验证集(Validation Set),然后将验证集(Validation Set)上效果最佳的模型置于测试集(Test Set)中测试,然后重复进行K次,泛化误差约等于K次测试误差的平均。
这种方法存在以下两个好处:
(1)所有的样本都在测试集中出现了一次,即不存在说服力不足的问题。
(我全都测了,总不可能说我故意选最容易评估的了吧!)
(2)训练数据集中的样本数据没有显著的减小。
(我只是在划分出来的训练集中再划分出一小部分做验证集),得出的模型效果会更加接近模型的真实泛化误差。
Reference:
- K折验证交叉验证_k折交叉验证_*Snowgrass*的博客-CSDN博客
- K-折交叉验证(记一个坑) - 知乎
- http://t.csdn.cn/8hgXy