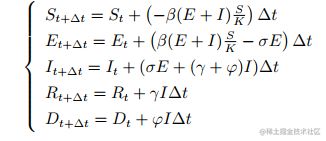Matlab基于SEIRD模型，NSIR预测模型，AHP层次分析法新冠肺炎预测与评估分析

全文链接：http://tecdat.cn/?p=32175

原文出处：拓端数据部落公众号

分析师：Jiahui Zhao

新型冠状病毒肺炎COVID-19 给中国乃至全世界都带来了深重的灾难，对世界经济也造成了不可逆的影响。该病毒传染性强、危害较大，需要我们高度警惕。国内目前疫情基本得到控制，但是为避免疫情反扑，我们有必要利用相关数学算法，结合大数据背景，开展相关分析，并提出有针对性地应对措施。

本文建立了SEIRD 模型， NSIR 预测模型，使用 AHP 层次分析法等进行了模拟仿真，评估疫情出现第二次高峰的风险大小，并给出复工复产的政策性建议，以避免第二次高峰的出现同时保障大型赛事的顺利举办。

模型假设

假设查找到的数据真实可靠。
假设无症状感染患者具有一定的传染能力。
假设指标的判定合理有效。
假设国家国情与政策的判断落实无误。
假设康复后的患者不再被感染。
假设偏远地区等无检测条件地区，视为无感染地区

模型求解

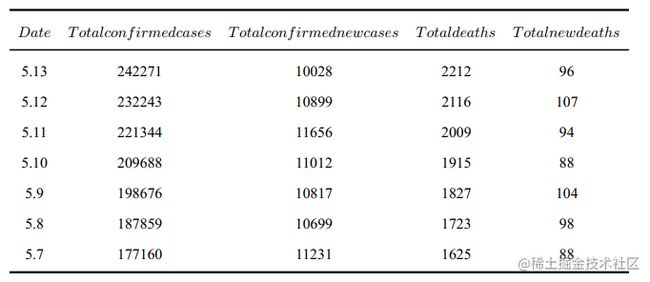
首先在 WHO 的官方网站上，我们整理收集了俄罗斯联邦从 5 月 7 日到 5 月 13 日新冠病毒肺炎有关人数，如表所示：

由以上数据可得，平均死亡率 φ 和平均治愈率 γ 分别为： 0.00913 和 0.992，平均潜伏期在 7 天左右。故： σ = 1/7 将微分方程转换成差分方程的形式：

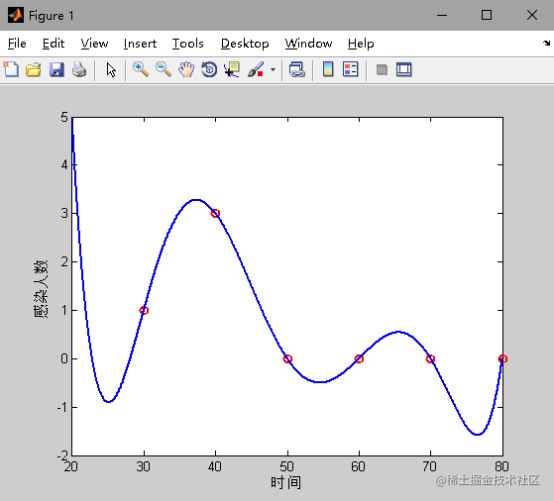
选取每天的数据，利用最小二乘法可以求出模型中所需参数，再将获得的参数代入SEIRD 模型，得到预测结果如图所示。根据模型的预测，可以看出在 5 月 13 日后，新增感染人数起起伏伏，情况恶劣，二次爆发几率极大。

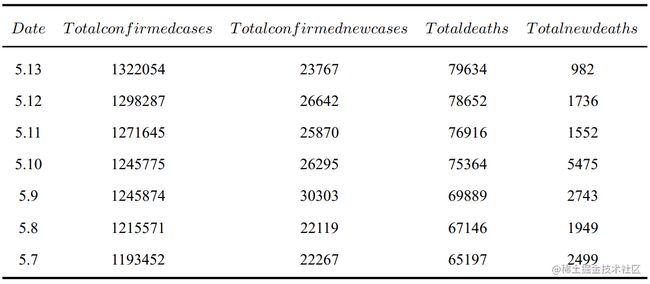
然后，我们整理收集了中国从 5 月 7 日到 5 月 1America 新冠病毒肺炎有关人数3 日新冠病毒肺炎有关人数，如表 3 所示：同理，选取每天的数据，利用最小二乘法可以求出模型中所需参数，再将获得的参数代入 SEIRD 模型，得到预测结果如图所示。根据模型的预测，可以看出在 5 月 13 日后，新增感染人数极少，曲线出现负数是模型的不完善处，二次爆发几率极低，可能会略微出现新病例。

最后，我们整理收集了美国从 5 月 7 日到 5 月 13 日新冠病毒肺炎有关人数，如表所
示：

同理，选取每天的数据，利用最小二乘法可以求出模型中所需参数，再将获得的参数代入SEIRD 模型，得到预测结果如图 4 所示。根据模型的预测，可以看出在 5 月 13 日后，美国疫情第一次高峰尚未达到，按先规模增长，有望达成群体免疫，无二次爆发

America 新冠病毒肺炎有关人数

America 的 SEIRD 模型预测图

问题二的模型建立与求解

层次分析法模型

一. 假阴性的影响因素

1. 病原学因素

若是病毒 RNA 的引物设计区域发生突变，可直接导致检测结果的假阴性。

2. 样本因素

2.1 采集样本的时间与类型不当

应采集患者发病 3 天内的标本，但多数患者潜伏期 2 7 天不等，绝大多数病患在就诊时
病程已经迁延了数天至数周，不能确定标本采集时是否为痰液、鼻、咽拭子等样本检测的最
佳时期，亦不能确认样本内病毒载量是否仍然处在方法学的检测范围内。

2.2. 样本质量低

合格的样本必须采集到含有病毒的细胞，且病毒含量能够达到核酸检测下限，否则将
导致检测结果出现假阴性。

2.3. 人员因素

由于核酸提取过程中手工操作较多，检测人员需要经过专业培训，具备基本的分子生
物学知识与熟练的实践技能。实验各位环节中，人为操作不当，会影响 PCR 结果的准确性。

2.4. 仪器设备因素

冰箱温度不稳定，会影响样本 RNA 的稳定性，导致假阴性。移液器量程不准确，反应
体系的不一致性和样本加样误差也是导致检测结果假阴性的原因之一。

层次分析法

层次分析法（Analytic Hierarchy Process 简称 AHP）是一种将与决策有关的要素分解成目标层、准则层和方案层，在此基础之上进行定性和定量分析，解决多目标的复杂问题的决策方法。

它是由美国运筹学家匹兹堡大学教授萨迪在 20 世纪 70 年代初期提出的，利用较少的定量信息使决策的思维过程数学化，从而为多目标、多准则或无结构特性的复杂决策问题提供简便的决策方法。

使用层次分析法进行综合评价的具体建模步骤如下：

Step1. 构建递阶层次模型，分解成目标层、准则层和方案层；
Step2. 构造判断矩阵和确定指标权重；
Step3. 单层次排序及并做一致性检验；
Step4. 层次总排序并进行一致性检验；
Step5. 如果层次总排序不能通过合理性检验，则需要重新判断或构建新的层次结构图，并且重新计算。

层次分析法对影响因素的排序分析

根据选取的假阴性、假阳性的影响因素建立层次结构模型运用层次分析方法解决影响因素排序的实际问题，先建立假阴性、假阳性的影响因素的层次模型。层次分析法首先要求决策者将决策问题根据其性质和隶属关系分化将元素分解成目标、准则、方案等层次设立递阶层次架构。
构造判断矩阵和确定指标权重构造判断矩阵，下表中的两个因素 i 和 j 分别表示两个进行比较的标准，标度 aij 为元素构成的矩阵称为两两对比矩阵。

模型求解

通过运用求和法求出每个矩阵对应的特征值及特征向量，并对其进行归一化，得到对应元素的向量矩阵然后对所求得的向量矩阵执行一致性检验，以获得指标下的权向量。然后，根据层次分析法的基本步骤，参考平均随机一致性指标 RI，运用 Excel 计算求解各层次单排序并进行一致性检验经过测算： CR = 0.034 < 0.1, CR_1 = 0.026 < 0.1，CR_2 = 0.017 < 0.1， CR_3 = 0.058 < 0.1, 有满意的一致性，通过一致性测试。

影响假阴性的因素排序：提取试剂因素 > 采集样本的时间与类型不当 > 样本质量低 > 扩增试剂因素 > 人员因素 > 仪器设备因素。

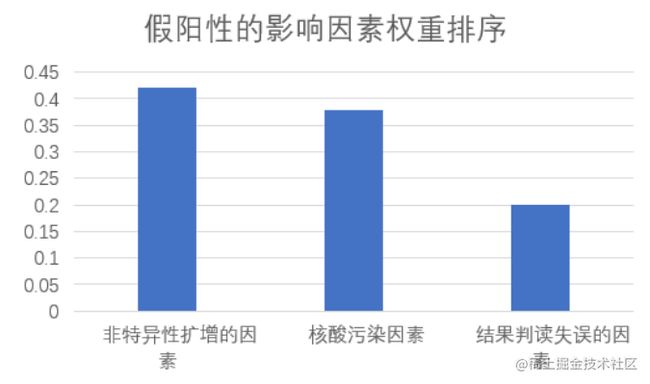
影响假阳性的因素排序：非特异性扩增的因素 > 核酸污染因素 > 结果判读失误的因素。

代码：



function [Q] =AHP(B)
%Q为权值，B为对比矩阵
%导入判别矩阵B
[n,m]=size(B) ;
%判别矩阵具有完全一致性
for i=1:n 
for j=1:n
if B(i,j)*B(j,i)~=1
end
end
%求特征值特征向量，找到最大特征值对应的特征向量
[V ,D]=eig(B) ;
tz= max(D) ;
tzz= max(tz) ;
c1=find(D(1,:)==max(tz));

tzx=V(:,c1);%特征向量
%权
quan=zeros (n,1) ;
for i=1 :n
quan(i,1)=tzx(i,1) / sum(tzx) ;
end
Q=quan ;
%一致性检验
CI=(tzz-n)/(n-1);
RI=[0,0,0.58,0.9,1.12,1.24,1.32,1.41,1.45,1.49,1.52,1.54,1.56,1.58,1.59] ;
%判断是否通过一致性检验
CR= =CI/RI(1,n) ;
if CR>=0. 1
fprintf('没有通过一致性检验\n');
else
fprintf('通过一致性检验\n');
end