「游戏」游戏服务器中AOI的原理及四叉树实现

前言

要不是想起来这篇文章想写一个关于游戏服务器开发过程中关于AOI相关的文章，我都差不点忘了我是一个游戏服务器开发人员。

之前一直写的都是关于Golang相关的源代码解析内容，今天也说一说关于游戏服务器开发中常用到的一些算法，以及相关的一些原理、实现等等。

因为我是个应届生，也处于学习阶段，对这个东西的理解不够深，如果有问题，请各位看官给予指正。在此表示感谢。

什么是AOI

AOI（Area Of Interest）翻译过来就是“感兴趣的区域”，这个玩意儿在很多的游戏中都会出现，比如在MMORPG游戏中，玩家走到某个场景的坐标（x，y）处，就需要通过AOI来获取到当前坐标处，一定范围内的所有玩家以及NPC、怪物（其实也算NPC的一种）的相关位置信息，交由客户端生成对应的模型渲染并且进行其之间的交互。

当玩家进行移动时，同时也会对玩家范围内的玩家进行广播位置同步，使得其他玩家知晓当前玩家进行的移动位置和移动范围。

当玩家进入一个游戏场景（地图、副本等）时，玩家所看到的各种各样的Entity（玩家，NPC，怪物皆算做Entity），都是通过服务器端的AOI系统在进行处理。显然,AOI实现算法的好坏，直接影响了当前游戏场景内所有玩家的游戏体验以及人数上限，如果AOI算法选择不好，那么可能会导致玩家在场景之中的一些游戏玩法产生不良效果，因此，选择一个优秀的AOI实现算法，是制作AOI系统的首要任务。

MMO类型的游戏都会有野外和主城场景，一般来说，服务器只会同步你周边多少半径以内的玩家给你，太远的一是玩家屏幕看不到没有意义，二是同步太多的玩家对于服务器压力成倍数上涨。

想象一下，如果一个区域内有100个人，这些人可能都在不停的走路，如果是广播形式的话，那每一个人移动都要向另外的100个人进行位置同步。假如服务器每50ms同步一次玩家位置，那么服务器处理100个人位置就需要
$$100\ast 100\ast 20=200000$$
次广播。这显然是无法承受的。那么为了降低这部分的服务器性能，就需要降低服务器同步的量级，一种解决方案就是AOI。核心概念就是只对那些感兴趣的观察者发送数据。

那么为了降低这部分的服务器性能，就需要降低服务器同步的量级，一种解决方案就是AOI。核心概念就是只对那些感兴趣的观察者发送数据。基于上面的例子而言，如果我们能把这个区域细分为10个，假定平均分配的情况下，每个区域里则只有10个人。那么此时每个人移动的时候，他就只要同步给同区域的10个人，大大减少需要同步的次数。同时，如果我们能充分利用现代CPU的核数，使用多线程来处理，则这个部分的性能损耗会大大的降低。

但这个方案同时也会带来额外的问题，比如a这个人，之前在A区域，现在移动到了B区域，那么就需要一个管理器来协调A和B两个AOI区域的数据更新。虽然区域划分的越多，需要同步的次数越少，但是同样的，管理的复杂度就越高。所以，AOI需要根据实际的游戏场景做到一个合理的平衡¹。

常见的AOI算法

在目前的游戏服务器开发领域，针对AOI的算法常见的有以下几种（本文基于2D游戏）：暴力法、灯塔算法、十字链表算法以及本文要重点介绍和实现的四叉树算法，上面几个算法各有不同，也各有优势，接下来我来介绍一下各个算法的基本原理以及其优势和缺陷。

暴力法

望文生义，所谓暴力法，就是不使用任何算法以及数据结构进行管理和组织，当玩家需要某个坐标点以及对应范围内的玩家列表时，暴力检索整个场景中的所有存在对象，然后进行坐标判断，随后返回给调用方的一种AOI实现算法，其检索的时间复杂度为O(n),该算法的优缺点如下：

优点

• 实现简单，不需要多余的复杂数据结构，每个场景保存一个数组作为存储玩家对象列表的数据结构即可
• 在少量Entity的地图场景之中（如小队副本，团队副本等），效率很高，且无需要复杂的数据结构

缺点

• 当场景中Entity数据量巨大，遍历整个数组会有很大的性能损耗
• Entity的场景进入、场景退出等相关操作需要频繁的操纵数组，数组本身对这种随机性的插入与删除的性能支持不佳
• 每次搜索单一Entity时，需要遍历整个数组

总结

暴力法的实现简单， 无需多余复杂数据结构，并且在少量Entity的场景中有着优秀的性能体现（这个有些歧义，因为相对于后续的某些*O(logn)*时间复杂度的算法来讲，*O(n)*的确不算优秀，但是综合时间复杂度和实现难度来讲，的确算一个性能平衡的算法），比如说LOL、王者荣耀等Moba游戏来说，双方队伍里仅有10名玩家，整个场景内的Entity不会过多，此时，暴力法的综合表现可能是比较好的（个人见解）。

灯塔算法

灯塔算法就是是把整个场景通过不同的粒度，利用网格划分成一个一个的大小相等的小区域， 在每个区域里树立灯塔。在Entity进入或退出格子时，维护每个灯塔上的Entity列表。灯塔好在哪？假设我们想知道某点周围10格内有哪些Entity，在没有灯塔的情况下，我们需要遍历所有的Entity计算其是否在范围内，随着地图内的Entity越来越多，查找的效率也会越来越差，所以我们需要一种方法来过滤那些明显不需要参与计算的Entity，所以我们将地图分割成一个个区域，在其中心放置一个假想的"灯塔"，每个"灯塔"都会保存区域内的Entity，这样当我们需要知道某点周围10格内有哪些Entity时，我们只需要计算出范围内有哪些"灯塔"，然后获取这些"灯塔"保存的Entity列表，针对这些Entity进行计算就能节省大量计算²。

优点

• 实现简单
• 相较于暴力法，灯塔法将大量Entity分散到了多个灯塔中，对于每个灯塔还是 *O(n²)*的复杂度，但由于把Entity数据量大量降了下来，所以性能要好的多

缺点

• 存储空间不仅和Entity数量有关，还和场景大小有关
• 浪费内存
• 且当场景规模大过对象数量规模时，性能还会下降。因为要遍历整个场景。对大地图不太合适

总结

灯塔法相较于暴力法进行了一些优化，使其场景内区分成不同的区域，每个区域的Entity数量就有了减少，也更快了，但是由于某些区域可能没有Entity存在，但是仍需要对其申请固定的内存，对内存有所浪费，且当场景规模大过对象数量规模时，性能还会下降。因为要遍历整个场景。对大地图不太合适。

十字链表算法

十字链表算法是根据二维地图，将其分成x轴和y轴两个链表。如果是三维地图，则还需要维护多一个z轴的链表。将对象的坐标值按照大小相应的排列在相应的坐标轴上面。所谓十字链表，即把地图坐标轴中的 X 和 Y 轴看成是2个链表，将玩家的 X 坐标按照从小到大插入 X 链表，将玩家的 Y 坐标按照从小到大插入 Y 链表，查询时根据玩家的坐标分别从2个链表中取出范围内的所有玩家，对两个玩家列表做交集，即为我们需要发送消息的玩家列表³。

优点

• 节省内存空间，没有Entity那么就不会占用内存空间
• 由于是有序链表，可以采用二分法进行快速搜索
• 由于链表特性插入和删除不会那么麻烦

缺点

• 大数据量的搜索性能还是有待提高、但是可以通过跳表等进行优化

四叉树算法

接下来我们讲解一下本篇文章最重要的部分，就是关于游戏AOI中的四叉树算法，四叉树其实在游戏AOI中不太常用（网上相关信息太少），经过查找一般都适用于地图的地形数据或者碰撞检测之类的地方，首先说一下什么是四叉树

四叉树

四元树又称四叉树是一种树状数据结构，在每一个节点上会有四个子区块。四元树常应用于二维空间数据的分析与分类。 它将数据区分成为四个象限。数据范围可以是方形或矩形或其他任意形状。

四叉树（quad-tree）是一种数据结构，是一种每个节点最多有四个子树的数据结构。

四叉树是在二维图片中定位像素的唯一适合的算法。因为二维空间（图经常被描述的方式）中，平面像素可以重复的被分为四部分，树的深度由图片、计算机内存和图形的复杂度决定。⁴。

我们都知道二叉树的变体二叉查找树，非常适合用来进行对一维数列的存储和查找，可以达到 O(logn) 的时间复杂度。当使用二叉树进行增删查时，只需要跟每个节点对比之后选择一条路线依次向下递归就可以找到所需插入或删除或者查找的对象。

但是由于二叉树只支持一维数据的问题，当面对游戏场景中需要X、Y两种方向的坐标时，显得并不是那么够用，因此，根据四叉树的特性，我们就可以使用四叉树来代替二叉树对X、Y两种方向坐标内容进行存储管理，同时还拥有着 O(logn) 的效率

四叉树在AOI中的使用

通过四叉树的特性，我们可以把其想象成一个正方形（矩形也行、本文按照正方形讲解）， 在最开始的树中，是只有一个根节点，没有任何子节点的，在树中的每个节点都会存储一个当前节点代表在地图中所覆盖的范围，当当前的跟节点中所存储的Entity数量大于N(一般来说取值128或64)且整个树的层次未超过D（一般取值为5）时触发扩容操作，此时，会根据公式将该节点所覆盖的范围均等的分为四分，分别为左上、右上、左下、右下四个格子，如图所示：

分割时，需要计算出四个子节点的覆盖范围， 而后根据覆盖范围，将上一层节点中存储的Entity根据其所处的坐标位置，分配到四个节点中的其中一个，这样之后，整棵树只有叶子节点存在Entity列表。当四个节点中的某个节点装满时并且深度也尚未达到最深，也就继续发生扩容操作：

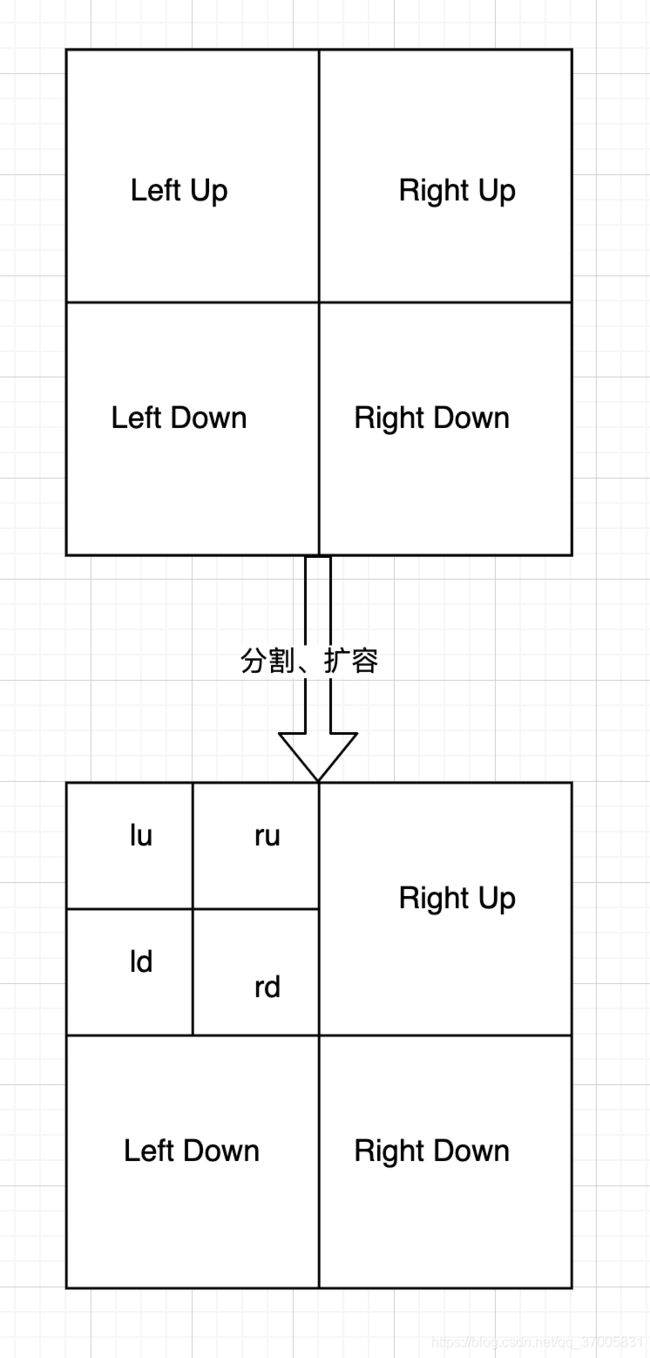
之后的操作以此类推，直到深度达到设定的最大上限后，叶子节点的Entity的容量将会不设限，否则会存不进去新的Entity。

在查找时，只需要根据要查找的节点（范围）一层一层的向下递归即可。

接下来我们随着代码以及图片来看一下具体的插入、删除、修改、和范围查询的过程原理及实现。首先看一下四叉树莓个结构体的节点的表示。

四叉树节点的表示

const (
  // 最大子树的个数
   maxChild        = 4
  // 每个子树的最大容量
   maxRoleCapacity = 128
  // 四叉树的最大深度
   maxDeep         = 5
)
// 记录根节点的变量
var root *Node

type Node struct {
   // 子节点 4叉树，所以4个子节点
   ChildNode [maxChild]*Node
   // 当前节点存储的数据
   Data *data
   // 当前节点包含范围
   currentArea
   // 当前深度
   Deep int
  // 是否为叶子节点
   Leaf bool
}
// 表示方位
// 这个比较适合调试使用 
// 实际没什么大用处
type azimuth int

const (
  // 当前子树的方位
  // 根为-1
  // 在数组中表示为0，1，2，3
	leftUp azimuth = iota
	rightUp
	leftDown
	rightDown
)
// 当前节点覆盖范围
type currentArea struct {
  // x的起始范围 这个点是这个格子的左上角
	XStart    float64
  // y的起始范围 这个点是这个格子的左上角
	YStart    float64
  // 当前区域宽度，因为是正方形 所以长==宽
	AreaWidth float64
}

func newNodeRange(xStart float64, yStart float64, width float64) currentArea {
	return currentArea{XStart: xStart, YStart: yStart, AreaWidth: width}
}
// 判断某个坐标是否在当前节点覆盖范围内
func (receiver *currentArea) intersects(x, y float64) bool {
	return (receiver.XStart <= x && x < (receiver.XStart+receiver.AreaWidth)) &&
		(receiver.YStart <= y && y < (receiver.YStart+receiver.AreaWidth))
}
// 看看当前节点的覆盖范围是否还可以均分为4份
func (receiver *currentArea) canBeCut() bool {
	return (receiver.XStart+receiver.AreaWidth)/2 > 0 &&
		(receiver.YStart+receiver.AreaWidth)/2 > 0
}
// 分割
func (receiver *currentArea) cut() [maxChild]currentArea {
	var child [maxChild]currentArea
	w := receiver.AreaWidth / 2
	child[leftUp] = currentArea{
		XStart:    receiver.XStart,
		YStart:    receiver.YStart,
		AreaWidth: w,
	}
	child[rightUp] = currentArea{
		XStart:    w + receiver.XStart,
		YStart:    receiver.YStart,
		AreaWidth: w,
	}
	child[leftDown] = currentArea{
		XStart:    receiver.XStart,
		YStart:    w + receiver.YStart,
		AreaWidth: w,
	}
	child[rightDown] = currentArea{
		XStart:    w + receiver.XStart,
		YStart:    w + receiver.YStart,
		AreaWidth: w,
	}
	return child
}

// 每个节点中存储数据的结构体
type data struct {
  // 这个
  // type Entity struct {
	//	X float64
	//	Y float64
	//	E string
	//	}
	d []*entity.Entity
}

func newNodeData() *data {
	return &data{
		d: make([]*entity.Entity, 0, maxRoleCapacity),
	}
}

func (receiver *data) Add(entity *entity.Entity) {
	receiver.d = append(receiver.d, entity)
}

func (receiver *data) Get(key string) (*entity.Entity, bool) {
	for i := 0; i < len(receiver.d); i++ {
		if receiver.d[i].E == key {
			return receiver.d[i], true
		}
	}
	return nil, false
}

func (receiver *data) Del(key string) {
	for i := 0; i < len(receiver.d); i++ {
		if receiver.d[i].E == key {
			receiver.d = append(receiver.d[:i], receiver.d[i+1:]...)
			return
		}
	}
}

func (receiver *data) Replace(old, new *entity.Entity) {
	for i := 0; i < len(receiver.d); i++ {
		if receiver.d[i].E == old.E {
			receiver.d[i] = new
			return
		}
	}
}

func (receiver *data) ClearAndEmpty() {
	receiver.d = nil
}

func (receiver *data) Len() int {
	return len(receiver.d)
}

// 循环使用
func (receiver *data) Range(f func(value *entity.Entity) bool) {
	for i := 0; i < len(receiver.d); i++ {
		if !f(receiver.d[i]) {
			return
		}
	}
}

插入

当有新的Entity插入时，需要从根节点与各个子节点进行比较，查看是否当前Entity的坐标处于该子节点中，如果处于则继续向下递归，直到处于叶子节点中保存，如果当前叶子节点需要扩容，那么就进行扩容操作后继续递归。

func (receiver *Node) AddToNode(entity *entity.Entity) {
   // 看看是否需要增长
   // 只有叶子节点需要增长
   if receiver.isLeafNode() && receiver.needGrow() {
      receiver.growTree()
   }
   // 如果是叶子节点 那就不要去搜孩子了
   if !receiver.isLeafNode() {
      receiver.ChildNode[receiver.findIndex(entity.X, entity.Y)].AddToNode(entity)
      return
   }
  // 叶子节点、直接保存
   receiver.Data.Add(entity)
}
// 通过二分法查这个传入的坐标属于哪个节点
func (receiver *Node) findIndex(x, y float64) azimuth {
  // 因为每个格子的左上角都是起始点
  // 那么 右下方的格子的左上角则是这个格子的中心
  // 那么就根据右下方个字的左上角去比较到底这个坐标在哪里
  // 这样只需要比两次就好
	if x < receiver.ChildNode[rightDown].XStart {
		if y < receiver.ChildNode[rightDown].YStart {
			return leftUp
		}
		return leftDown
	}
	if y < receiver.ChildNode[rightDown].YStart {
		return rightUp
	}
	return rightDown
}


// 查看是否需要扩容
// 扩容条件为
// 1:当前节点的数据+1后超出最大容量
// 2:当前深度+1后不超过设定的最大深度
// 3:当前覆盖范围仍可切分
func (receiver *Node) needGrow() bool {
	return ((receiver.capacity() + 1) > maxRoleCapacity) &&
		(receiver.getDeep()+1 <= maxDeep) && receiver.canBeCut()
}
// 树的分割、增长
func (receiver *Node) growTree() {
  // 拿到分割后的覆盖范围
	newRange := receiver.cut()
  // 既然扩容了当前节点就不是叶子节点了
	receiver.Leaf = false
  // 遍历四个子节点
	for i := 0; i < maxChild; i++ {
    // 为这个子节点构建一个新的对象并使得其深度+1
		receiver.ChildNode[i] = newTreeNode(newRange[i].XStart, newRange[i].YStart,
			newRange[i].AreaWidth, receiver.Deep+1)
    // 遍历当前节点数据
    // 找到符合当前子节点范围内的数据，放进去
		receiver.Data.Range(
			func(value *entity.Entity) bool {
				if receiver.ChildNode[i].intersects(value.X, value.Y) {
					receiver.ChildNode[i].Data.Add(value)
				}
				return true
			})
	}
  // 清空当前节点的数据
	receiver.Data.ClearAndEmpty()
}

删除

删除的话就很简单了，跟插入的方式一样，只不过去掉了扩容操作以及将添加变为了删除

func (receiver *Node) DelFromNode(x, y float64, key string) {
   // 如果是叶子节点 那就不要去搜孩子了
   if !receiver.isLeafNode() {
      receiver.ChildNode[receiver.findIndex(x, y)].DelFromNode(x, y, key)
      return
   }
   receiver.Data.Del(key)
}

删除的话还有一个优化方案，就是此节点及其兄弟节点的Entity被删除后的总Entity数量小于设定的容量。则会产生缩容操作，这样可以减少一层的递归，但是此代码还没来得及写那个优化方案，在此算作一个TODO。

修改

修改的话其实和上面两个也差不多直接看代码吧

// 传入要修改的和修改后的实体
func (receiver *Node) Modify(from,to *entity.Entity) {
   if receiver.isLeafNode() {
     // 看看这个实体在没在存储中
      _, ok := receiver.Data.Get(k)
      if ok {
        // 如果修改后的实体也在当前叶子节点范围内 
        // 直接替换就好
         if receiver.intersects(to.X, to.Y) {
            receiver.Data.Replace(from,to)
            return
         }
        // 否则从此节点删除然后从根节点执行一次插入操作
         receiver.Data.Del(from.E)
         root.AddToNode(to)
         return
      }
      return
   }
    // 一直递归找到覆盖了from坐标的哪个叶子节点
   receiver.ChildNode[receiver.findIndex(from.X(), from.Y())].Modify(from, toX, toY)
}

范围查找

增、删、改、都说完了其实具体实现也都差不多，我们利用四叉树主要的原因是利用其查找的时间复杂度为O(logn)，并且在游戏中很少出现直接查找某个坐标点的单一查找的情况、几乎都是范围查找，因此范围查找是此次介绍的重要的地方，直接上代码，根据代码来讲解更快一些

func (receiver *Node) SearchEntities(result *[]*entity.Entity, e *entity.Entity,r float64) {
   // 一路往下搜 直到搜到叶子节点
   if !receiver.isLeafNode() {
     // 四个叶子节点
      for i := 0; i < maxChild; i++ {
        // 算出要查的范围
        // 最终yMin,yMax,xMin,xMax可以形成一个矩形范围
        // （xMin, yMin）(xMin, yMax)(xMax, yMin)(xMax, yMax) 
        // 分别可以定位到这个矩形范围的左上角，左下角，右上角，右下角
        // 只要子节点的覆盖范围中包含这四个点的任意一点
        // 就说明该子节点里包含有需要遍历的数据
         x, y := e.X, e.Y
         xMin, xMax := x-r, x+r
         yMin, yMax := y-r, y+r
				// 在每个节点中查询边界是否存在于这个子节点中
        // 存在则进入这个子节点去遍历
         if receiver.ChildNode[i].intersects(xMin, yMin) || receiver.ChildNode[i].intersects(xMin, yMax) ||
            receiver.ChildNode[i].intersects(xMax, yMin) || receiver.ChildNode[i].intersects(xMax, yMax) {
            receiver.ChildNode[i].SearchEntities(result, e, r)
         }
      }
      return
   }
  // 遍历到了叶子节点 就进去搜集数据
   receiver.search(result)
}

func (receiver *Node) search(result *[]*entity.Entity) {
  // 把叶子节点的数据都塞进去
  // 其实此处应该去再次筛选范围内的数据的
	// 但是由于矩形的筛选范围一定局限性
  // 为了一定的容错性
  // 所以取出当前节点所有数据
	receiver.Data.Range(
		func(value *entity.Entity) bool {
      *result = append(*result, value)
			return true
		})
	return
 }

总结

四叉树算法的一些原理及其实现大概就讲完了，讲了这么多，其实就搜索性能来讲四叉树与灯塔算法的搜索性能差不多，但是相较其优势时针对内存的占用，因为灯塔算法时一次性开辟所有内存，无论其格子内是否包含数据，而四叉树则可以在没有数据的地方不开辟内存。相较于十字链来说插入、删除性能无需遍历整个十字链而是按照树型遍历时间复杂度为O(logn)，而十字链为O(n)，Entity数量不多的情况下没什么关系，一旦场景内Entity数量巨大会导致很长时间的搜索延迟。

总结

常用的AOI算法到这里就讲完了，虽然不同的算法之间的优缺点各不相同，但是也不能说其完全不堪大用，最终的算法选择还是需要根据实际的业务逻辑来考虑，比如MOBA游戏的10人场景就没必要采用四叉树遍历，因为实现复杂，暴力法即可快速的完成。

这是作者第一次写游戏相关的文章，同时目前也处于学习过程中。如果有那里有些错误请各位留言指教，谢谢！

我已开通自己的公众号【Echo的技术笔记】
日后的文章发布会主要在公众号上发布
希望各位关注一下
谢谢大家啦

参考文献

---

1. Unity手游实战：从0开始SLG——世界地图篇（十一）AOI https://cloud.tencent.com/developer/article/1659098 ↩︎

2. 灯塔AOI简易实现](https://www.cnblogs.com/silvermagic/p/9373414.html) ↩︎

3. 聊聊游戏中的AOI https://iyichen.xyz/2020/04/talk-about-aoi/ ↩︎

4. 四叉树 https://baike.baidu.com/item/%E5%9B%9B%E5%8F%89%E6%A0%91 ↩︎