【数据结构】树的认识
一个人的未来不是预测出来的,而是创造出来的。 -- 亚当·詹姆斯
目录
前言:
一.什么是树?
二.树有什么用?
❤️1. 数据库
2. 文件系统
3. 编程语言
4. 网络
5. 人工智能
三.树的基础知识
四.树的存储结构
1.双亲表示法
2.孩子表示法
3.孩子兄弟表示法
前言:
前面我们学习了,顺序表,链表,栈和队列,它们都是一对一的线性结构,但是往往还有一对多的情况,这就是我们今天要学习的一对多的数据结构:树(Tree)。树比前面的数据结构学起来要难一点,希望大家能够反复的学习,达到熟能生巧。
学习树的知识框架:![]()
一.什么是树?
想到树,大家可能都会想到现实中的树,各种各样的树,就像下面这样,这是一颗很漂亮的树。
而今天我们要学习的数据结构的树是怎么样的呢?
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
有一个特殊的结点,称为根结点,根节点没有前驱结点,除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继。因此,树是递归定义的。
这个结构就是一个树,它是不是很像现实中的树,给倒过来的。我想它之所以叫树,可能也是这个原因吧。
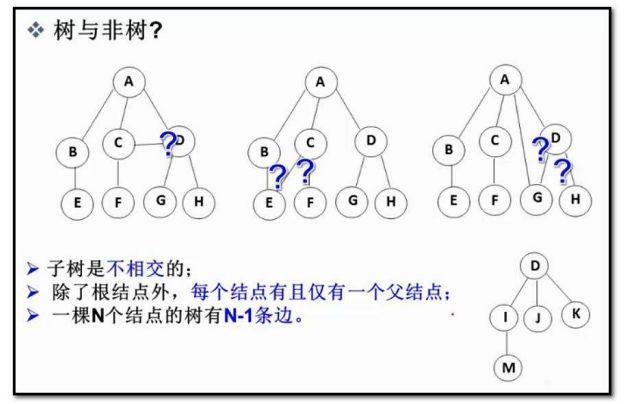
注意:树的子树之间不能有交集。就像下面这样:
打?的地方,子树之前发生了交集,这样是不可以的,如果这样,它就不能称作为树。
二.树有什么用?
数据结构树的应用:
数据结构是计算机科学中重要的一个分支,而树是其中一种重要且实用的数据结构之一。树是由一个根节点和若干子节点组成的一种非线性数据结构,被广泛应用于计算机领域中,特别是在算法设计和数据处理方面。下面我们将详细介绍树的应用领域。
注意:下面的树的应用都是高阶的数据结构的树,C++才会学习。
❤️1. 数据库
在数据库管理系统中,树被广泛应用于索引结构。数据库中的查找过程可以转化为在树中查找某个节点的过程。常用的树结构包括B-树、B+树和红黑树,这些结构可以高效的处理大量数据,支持高效的检索和排序。
2. 文件系统
操作系统中的文件系统其实就是一种树形结构。目录和文件被视为节点,而目录之间的关系和文件之间的关系则是树的关系。基于树形结构的文件系统使得我们可以很方便地在系统中查找和管理文件。
下面就是操作系统的文件系统,它就是一种树形的结构,使用树来实现。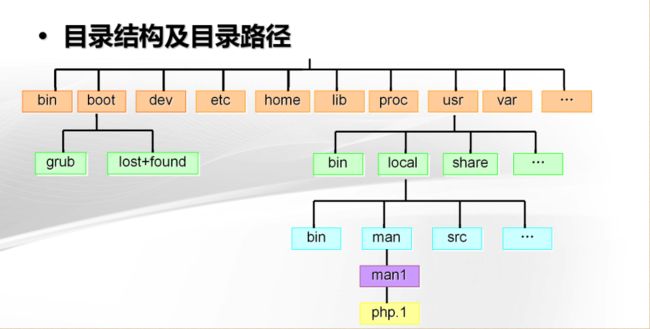
3. 编程语言
树形结构被广泛运用于编程语言中。AST(抽象语法树)就是一种常见的语法分析树,它将程序中的语句和表达式抽象成一个树形结构,在编译器中被广泛使用,可以很方便地实现代码的词法分析、语义分析和优化。此外,树也可以用于构建运行时数据结构,如二叉搜索树、Trie树、AVL树等等。
4. 网络
在计算机网络中,树的结构被广泛应用于路由器和交换机中。这些设备需要通过识别和分析网络中的数据包,将它们分配到不同的路由或交换机上进行处理。树的结构使得这些设备可以很方便地对不同的数据包进行分类、处理和转发。
5. 人工智能
在人工智能中,树也是非常重要的一种数据结构。决策树是常用的机器学习算法之一,它通过一系列的二叉树形结构对数据进行分类和判断。在处理自然语言、语音识别和图像处理等领域中,树结构也被广泛应用。
总之,数据结构树在计算机领域中有着非常广泛的应用,可以用于解决各种问题。从数据库、文件系统到编程语言、网络和人工智能等领域,都需要树这种数据结构来达到高效、快速、准确处理数据的目的。因此,学习并掌握树这种数据结构非常重要,可以帮助我们更好地理解计算机领域内的各种问题和算法。
三.树的基础知识
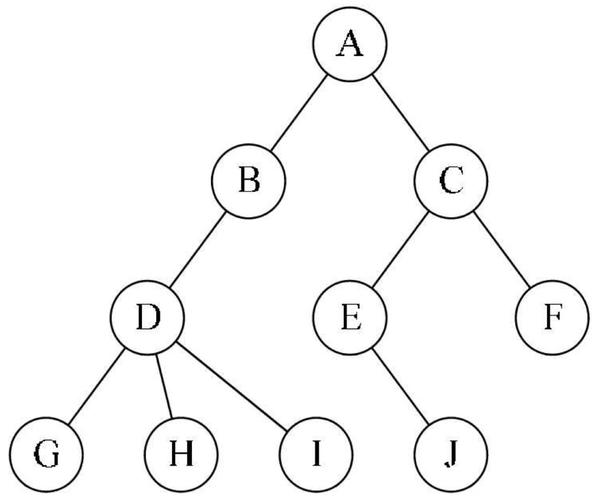
节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6。
叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I...等节点为叶节点。
非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G...等节点为分支节点。
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点。
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;如上图:B是A的孩子节点。
兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点。
树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6。
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推。
树的高度或深度:树中节点的最大层次; 如上图:树的高度为4。
堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点。
节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先。
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
森林:由m(m>0)棵互不相交的树的集合称为森林。
总结:上述的这些都是关于树的一些基础知识,你不必刻意的去记忆,这些概念就像人类的亲缘关系一样,多看见几遍也就记住了。
现在我们是先初入树,先了解一些树的基本知识,为了方便后面学习二叉树。
四.树的存储结构
说到存储结构,这就不得不想起之前学过的顺序和链式两种存储结构。先看看顺序存储结构,用一段地址连续的存储单元依次存储线性表的数据元素,这对于一对一的线性的数据结构,很容易办到,但是对于一对多的的树结构呢?又该如何存储呢?
树的某个节点的孩子可能有多个,这就意味着,无论按何种顺序将树中的所有结点存储到数组中,结点的存储位置都无法直接反应逻辑关系。因为将数据元素挨个存储在数组中,我们无法知道他们的关系,谁是谁的孩子,谁又是谁的双亲,完全不知道。显然这样存储树是不行的。
但是我们充分利用顺序和链式存储结构的特点。完全可以实现对树的存储结构的表示,接下来我们就会介绍三种表示方法:双亲表示法,孩子表示法,孩子兄弟表示法。
1.双亲表示法
在树的结构中,除了根结点,每一个结点不一定有孩子结点,但是都会有双亲结点,所以我们就使用双亲表示法来实现。
我们使用一段连续的空间存储树的结点,同时在每个结点中,一个是自己的数值域,另一个是自己双亲的下标。
由于根结点没有双亲,我们约定根结点的双亲结点的下标为-1。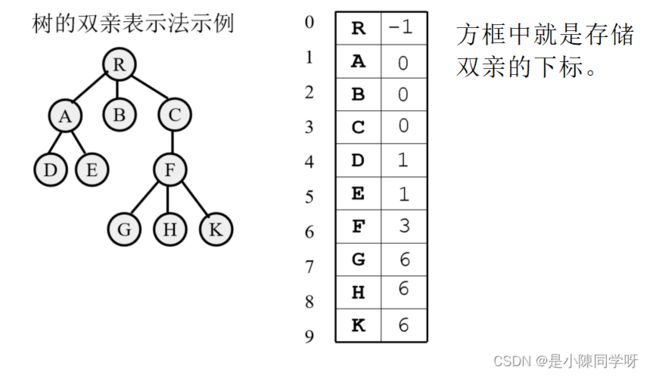
代码实现:
#define MAX 100
typedef int TETypeData;
typedef struct PTnode
{
TETypeData data;//自己的数据域
int parent;//双亲的下标
}PTnode;
typedef struct PTree
{
PTnode arr[MAX];
int r;//根的位置
int n;//结点数
}PTree;虽然这样可以很容易表示出来树的结构,但是如果们要知道某个结点的孩子,或者某个结点的兄弟,这样无法表示了,所以双亲表示法是有很大弊端的。所以这个表示方法基本上是不用的。
2.孩子表示法
由于一个结点可能有多个子树,我们可以考虑多重链表的方式,即每个结点有多个指针域,其中每个指针指向一颗子树的根结点,我们把这种方法叫做多重链表表示法。
方案一:
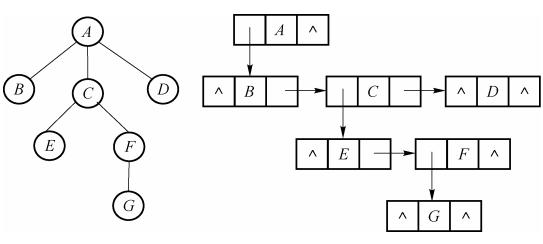
一种是指针域的个数就是树的度,树的度就是最大的那个结点的度。结构如下图所示:
可以看出每一个结点的度是不一样的,^就表示空的指针域,就是浪费的空间。如果每个结点的度相差很小时,这样的结构也能充分的利用空间。那为什么我们不能按需给分配空间呢?那就有了第二种方案。
方案二:
每个结点的指针域的个数等于该结点的度,这样就能按需给分配空间了。如下图所示:
这个方法就减少了空间的浪费了,大大的提高了空间的利用率。但是由于各个结点的链表时不同的结构,加上还要维护结点的值,这就非常的麻烦了。所以接下来我们介绍孩子表示法。
具体方法:
我们把每个结点的孩子结点排列起来,以单链表的形式给存储起来,则n个结点有n个孩子链表,如果是叶子结点则表示单链表为空。然后n个头指针又组成一个线性表,采用顺序存储的方式存储到一个数组中去。
我们设置两种结点结构,一个是表头的结构,data存储数值域,firstchild为头指针域。
另一个是孩子链表。child存储某个结点在表头数组中的下标,next指向下一个孩子的指针。
具体结构如下:
#define MAX 100
typedef int TETypeData;
typedef struct CTNode {
int child;//在表头中的下标
struct CTNode* next;//指向下一个孩子的指针
}CTNode;
typedef struct CThead//表头的结构
{
TETypeData data;//数据域
CTNode* firstchild;//头指针域
}CThead;
typedef struct CTree
{
CThead arr[MAX];//结点的数组
int r;//根结点的位置
int n;//结点数
}CTree;感觉是不错了,但是还是没办法知道某个结点的双亲是谁,上述的表示的方法都是不完美的,总是有缺陷。接下来我们就上孩子兄弟表示法。
3.孩子兄弟表示法
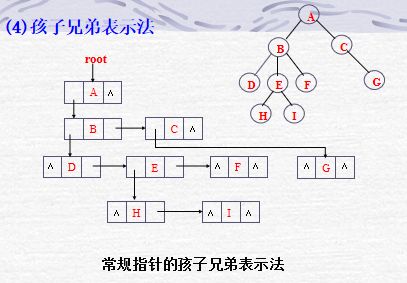
任意一颗树,它的结点的第一个孩子如果存在就是唯一的,它的右兄弟如果存在也是唯一的。因此,我们设置两个指针,分别指向该结点的第一个孩子和此孩子的右兄弟,我们称为左孩子右兄弟。它的结构如下:
代码实现:
typedef int TETypeData;
typedef struct Tree
{
TETypeData data;
strcut Tree* leftchild;
strcut Tree* rightchild;
}Tree;可以看出,结点的指针总是指向它的第一个孩子,然后第一个孩子指向它的兄弟,兄弟再指向他的兄弟,以此类推,把整个树的结构给表示出来。这种方法虽然也不能把某个的结点的双亲表示出来,但是这个表示法把一颗复杂的树表示为了一颗二叉树。这就是我们后面的重点内容。