NX/UG二次开发—3D几何—包围盒相交检测（转载）

一：包围盒介绍

包围盒是指能够包容物体的三维立方体或者二维长方形，是包围体的一种，常常用于模型的碰撞检测。包围体主要包括球体、轴对齐包围盒(AABB)、有向包围盒(OBB)和凸包(Convex Hull)。

转载地址：Bounds(包围盒)详解-【AABB包围盒、Sphere包围球、OBB方向包围盒、FDH固定方向凸包】_隨意的風的博客-CSDN博客_obb包围盒

1.1 AABB包围盒(Axis-aligned bounding box)

     AABB是应用最早的包围盒。它被定义为包含该对象，且边平行于坐标轴的最小六面体。故描述一个AABB，仅需六个标量。AABB构造比较简单，存储空间小，但紧密性差，尤其对不规则几何形体，冗余空间很大，当对象旋转时，无法对其进行相应的旋转。处理对象是刚性并且是凸的，不适合包含软体变形的复杂的虚拟环境情况。
        AABB也是比较简单的一类包围盒。但对于沿斜对角方向放置的瘦长形对象，其紧密性较差。由于AABB相交测试的简单性及较好的紧密性，因此得到了广泛的应用，还可以用于软体对象的碰撞检测。

1.2 包围球(Sphere)

       包围球被定义为包含该对象的最小的球体。确定包围球，首先需分别计算组成对象的基本几何元素集合中所有元素的顶点的x，y，z坐标的均值以确定包围球的球心，再由球心与三个最大值坐标所确定的点间的距离确定半径r。包围球的碰撞检测主要是比较两球间半径和与球心距离的大小。

1.3 OBB方向包围盒(Oriented bounding box)

      OBB是较为常用的包围盒类型。它是包含该对象且相对于坐标轴方向任意的最小的长方体。OBB最大特点是它的方向的任意性，这使得它可以根据被包围对象的形状特点尽可能紧密的包围对象，但同时也使得它的相交测试变得复杂。OBB包围盒比AABB包围盒和包围球更加紧密地逼近物体，能比较显著地减少包围体的个数，从而避免了大量包围体之间的相交检测。但OBB之间的相交检测比AABB或包围球体之间的相交检测更费时。

1.4 FDH固定方向凸包(Fixed directions hulls或k-DOP)

      FDH（k-DOP）是一种特殊的凸包，继承了AABB简单性的特点，但其要具备良好的空间紧密度，必须使用足够多的固定方向。被定义为包含该对象且它的所有面的法向量都取自一个固定的方向(k个向量)集合的凸包。FDH比其他包围体更紧密地包围原物体，创建的层次树也就有更少的节点，求交检测时就会减少更多的冗余计算，但相互间的求交运算较为复杂。

二：OBBP碰撞检查

转载地址：

OBB2D相交检测_[奋斗不止]的博客-CSDN博客

2-1判断2D平面上两个矩形(可以旋转)是否相交？

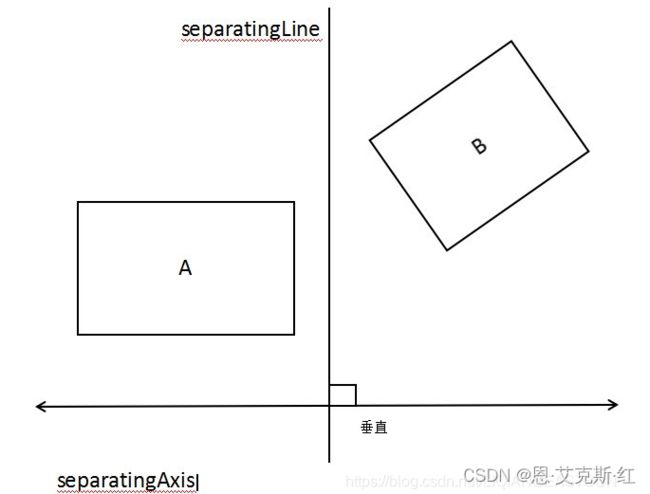
如果两个矩形 A、B 不相交，则存在至少一条直线能够将两个矩形分割在两侧。对于凸多边形依然成立。能将两个矩形分割的直线叫分离线 separatingLine、垂直于分割线的直线叫分离轴 separatingAxis
如下图

 如何确定是否有一条能够分割两个矩形，它又在哪里。
经过科学的证明如果存在能够将两个矩形分割的线，则至少有一条线是平行于两个矩形的一条边。
则 separatingAxis 也平行于两个矩形的某一条边。我们只需要证明这四条线。

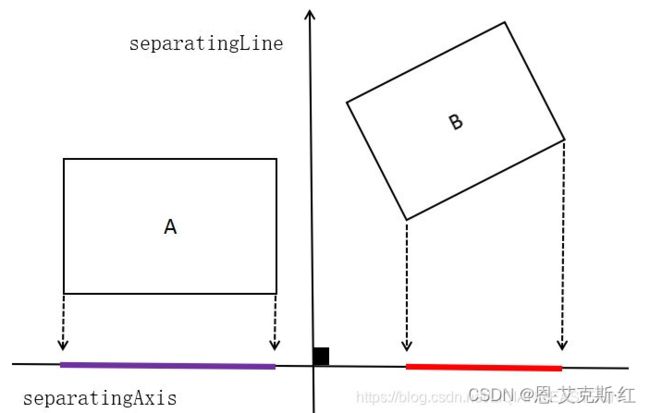
 如果两个矩形不相交，则A、B 在 separatingAxis 上的投影没有重合部分，看下图紫色、红色线段就是两个矩形在分割轴上的投影

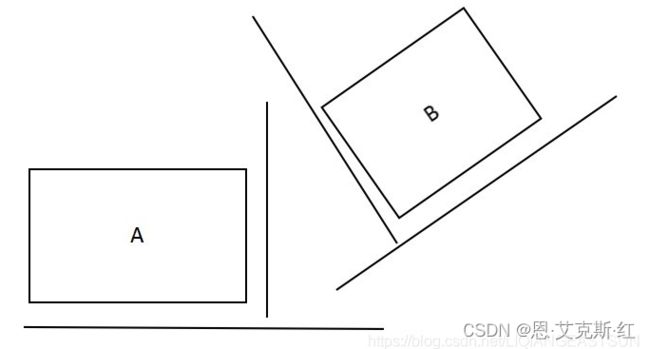
 看下图A、B分别在 separatingAxis1 和 separatingAxis2上投影，
在separatingAxis1 上紫色和红色投影相交了，则separatingAxis1 不是A、B的分离轴，不能判定A、B是否相交。
在separatingAxis2 上绿色和蓝色投影不相交，则separatingAxis2 是A、B的分离轴，可以判定A、B不相交。

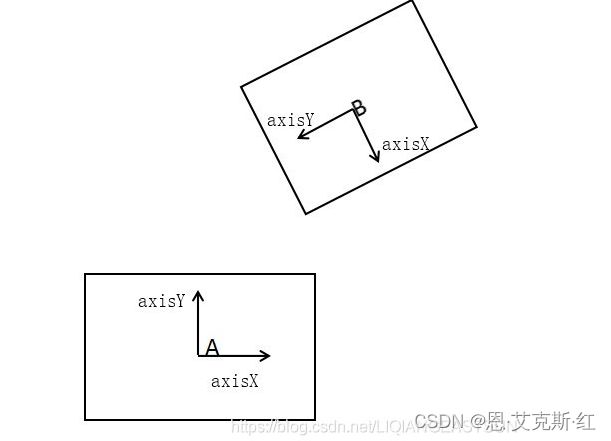
 首先确认需要判断的四个分离轴，下图中 A、B 的axisX、axisY

将 A 的四个顶点在分离轴上做投影，保存一个最小值 a_minT，一个最大值 a_maxT，则A在分离轴上的投影范围是 [a_minT，a_maxT]

同理，将 B 的四个顶点在分离轴上做投影，保存一个最小值 b_minT，一个最大值 b_maxT，则B在分离轴上的投影范围是 [b_minT，b_maxT]
看下图，以 B 为例，四个顶点A、B、C、D 分别向轴上做垂线， a < b < c < d，则最终B的投影范围为(a，d)

 a、b、c、d的值如何计算？
令 axis 为计算的轴， A坐标、B坐标、C坐标、D坐标 为一个 OBB的四个顶点，每个顶点分别点乘 axis 得到值
a = Dot(A坐标， axis)
b = Dot(B坐标， axis)
c = Dot(C坐标， axis)
d = Dot(D坐标， axis)
minT = Math.min(a，b，c，d)
maxT = Math.max(a，b，c，d)

2-2判断3D空间内两个box(可以旋转)是否相交？

在2D 中是只要有一个轴、线将两个 OBB 分离到两侧就判定两个 OBB不相交

在3D 中基本类似2D，但是在3D 中要将分离线替换为分离面，就是只要是找到一个面，能将两个 OBB分离在面的两侧，就说明两个OBB不相交。看下图

面P平行于OBB的一个面 ABCD，面P可以将两个 OBB分离到两侧
 

 像面P这样的面理论上可以找到几个？

 除了平行于面的面还有下面这种，下面这个将两个OBB分离的面的法向量是 两个红色边叉乘得到的

 

两个OBB分别命名为 A、B

则 A 有三个轴 a_axisX，a_axisY, a_axisZ

则 B 有三个轴 b_axisX，b_axisY, b_axisZ

总共有 9 中组合分别为

cross1 = a_axisX 叉乘  b_axisX

cross2 = a_axisX 叉乘  b_axisY

cross3 = a_axisX 叉乘  b_axisZ

cross4 = a_axisY 叉乘  b_axisX

cross5 = a_axisY 叉乘  b_axisY

cross6 = a_axisY 叉乘  b_axisZ

cross7 = a_axisZ 叉乘  b_axisX

cross8 = a_axisZ 叉乘  b_axisY

cross9 = a_axisZ 叉乘  b_axisZ

所以在3D轴分离轴总共有 6 + 9 = 15 中。

点到分离轴的投影方式同 2D 计算相同，只是点坐标和向量的 Vector2 调整为 Vector3

2D 中一个OBB 有两个轴，四个顶点

3D 中一个OBB 有三个轴，八个顶点

参考源码见转载博客：OBB3D相交检测_[奋斗不止]的博客-CSDN博客_判断两个3维box相交接上一篇OBB2D相交检测在2D 中是只要有一个轴、线将两个 OBB 分离到两侧就判定两个 OBB不相交在3D 中基本类似2D，但是在3D 中要将分离线替换为分离面，就是只要是找到一个面，能量两个 OBB分离在面的两侧，就说明两个OBB不相交。看下图面P平行于OBB的一个面 ABCD，面P可以将两个 OBB分离到两侧像面P这样的面理论上可以找到几个？首先平行于每个OBB六个面的，因为一个OBB的六个面是俩俩平行的，所以一个OBB可以贡献 3 个面，两个OBB可以贡献 6个面。看下..https://blog.csdn.net/LIQIANGEASTSUN/article/details/119611263

三：AABB碰撞检查

 

 

 测试运行速度，4435个面，转换成OBB无向包围盒，并与第一个盒子进行碰撞检查，计算边界盒子大约4.01s，碰撞检测用时0.07s：