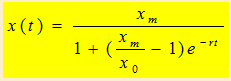数学建模——人口增长模型的matlab实现以及对2010年人口预测
文章目录
-
- 运行软件:MATLAB R2012a
- 实验数据
- 指数增长模型
-
- 指数增长模型:方法一
-
- 对2010年的人口预测
- 指数增长模型:方法二
-
- 对2010年人口预测
- 改进的指数增长模型
-
-
- 对2010人口预测
-
- 逻辑斯蒂(logistic)模型
-
- 逻辑斯蒂(logistic)模型:方法一
-
- 对2010预测
- 逻辑斯蒂(logistic)模型:方法二
-
- 对2010预测
运行软件:MATLAB R2012a
实验数据
| 年份 | 1790 | 1800 | 1810 | 1820 | 1830 | 1840 | 1850 | 1860 |
|---|---|---|---|---|---|---|---|---|
| 人口/百万 | 3.9 | 5.3 | 7.2 | 9.6 | 12.9 | 17.1 | 23.2 | 31.4 |
| 增长率/10年 | 0.2949 | 0.3113 | 0.2986 | 0.2969 | 0.2907 | 0.3012 | 0.3082 | 0.2452 |
| 年份 | 1870 | 1880 | 1890 | 1900 | 1910 | 1920 | 1930 | 1940 |
|---|---|---|---|---|---|---|---|---|
| 人口/百万 | 38.6 | 50.2 | 62.9 | 76.0 | 92.0 | 105.7 | 122.8 | 131.7 |
| 增长率/10年 | 0.2435 | 0.2420 | 0.2051 | 0.1914 | 0.1614 | 0.1457 | 0.1059 | 0.1059 |
| 年份 | 1950 | 1960 | 1970 | 1980 | 1990 | 2000 | 2010 |
|---|---|---|---|---|---|---|---|
| 人口/百万 | 150.7 | 179.3 | 203.2 | 226.5 | 248.7 | 281.4 | 308.7 |
| 增长率/10年 | 0.1579 | 0.1464 | 0.1161 | 0.1004 | 0.1104 | 0.1349 |
指数增长模型
满足人口增长的微分方程和初始条件为:
![]()
利用函数dsolve()可得:
![]()
指数增长模型:方法一
根据已知数据对模型的参数进行估计又称为数据拟合。
对下面的这个公式同时取对数
![]()
可得
![]()
t:代表年份1970取0,依次类推
x:人口数量,实验数据已知
根据求出的公式可以求出y;然后利用polyfit()函数求出r,a的值;当a求出来时,根据上面求出的公式,可以求出x0;将r,x0带入公式![]()
可求出指数增长模型方法一的x值
代码如下:
使用的是matlb函数
function [ x1 ] = method_1( x )
%方法一:直接用人口数据和线性最小二乘法
% 利用函数polyfit(),dsolve()求解,r年增长率,返回x1模型的估计值
y=log(x);
t=0:1:21;
p=polyfit(t,y,1);
r=p(1);
a=p(2);
x0=exp(a);
s=dsolve('Dx=r*x','x(0)=x0','t');
x1=eval(s);
x1=x1';
end
运行代码:
x=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76 92 105.7 122.8 131.7 150.7 179.3 203.2 226.5 248.7 281.4];
m=1790:10:2000;
m=m';
m(:,2)=x';
m(:,3)=method_1(x);
运行界面:

运行结果:第一列代表年份;第二列代表实际人口;第三列为指数增长模型:方法一的预估值
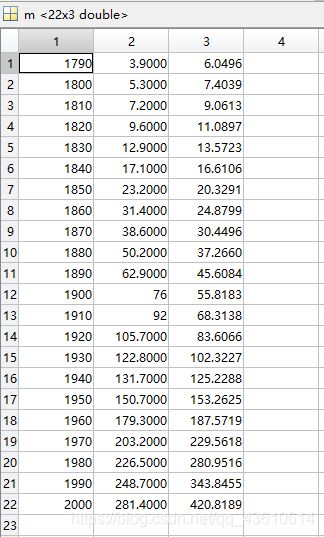
对2010年的人口预测
根据上面算出的结果,可以得到:r=0.2020 x0=6.0496
直接利用算出来的参数计算2020年的结果(t=22)
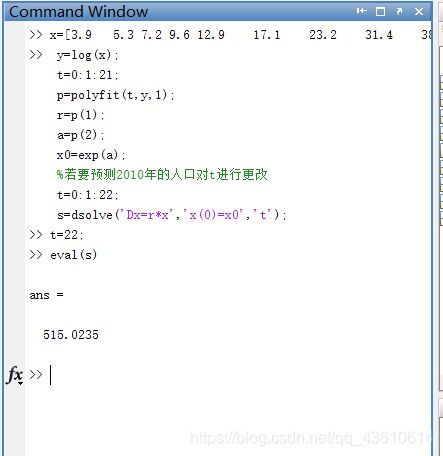
运行代码:
>> x=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76 92 105.7 122.8 131.7 150.7 179.3 203.2 226.5 248.7 281.4];
>> y=log(x);
t=0:1:21;
p=polyfit(t,y,1);
r=p(1);
a=p(2);
x0=exp(a);
%若要预测2010年的人口对t进行更改
t=0:1:22;
s=dsolve('Dx=r*x','x(0)=x0','t');
>> t=22;
>> eval(s)
指数增长模型:方法二
先对人口数据进行数值微分,再计算增长率并将其平均值作为 的估计; 直接取原始数据。
公式:

先求rk,再求出r,再根据公式![]()
求出模型的预估值
代码如下:
我是以函数文件运行:
function [ x2 ] = method_2( x )
%方法二:先对人口数据作数值微分,再计算增长率并将其平均值作为r的估计;x0直接采用原数据
n=length(x);
t=0:1:n-1;
rk=zeros(1,n);
rk(1)=(-3*x(1)+4*x(2)-x(3))/2;
rk(n)=(x(n-2)-4*x(n-1)+3*x(n))/2;
for i=2:n-1
rk(i)=(x(i+1)-x(i-1))/2;
end
rk=rk./x;
r=sum(rk)/n;
x2=zeros(n,1);
x2(1)=x(1);
for i=1:n
x2(i)=x2(1)*exp(r*t(i));
end
end
运行代码
x=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76 92 105.7 122.8 131.7 150.7 179.3 203.2 226.5 248.7 281.4];
m=1790:10:2000;
m=m';
m(:,2)=x';
m(:,3)=method_1(x);
m(:,4)=method_2(x);
运行界面:

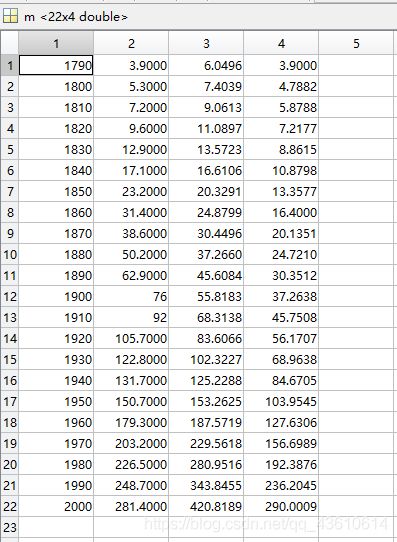
运行结果:第一列代表年份;第二列代表实际人口;第三列为指数增长模型:方法一的预估值;第四列为指数增长模型:方法二的预估值
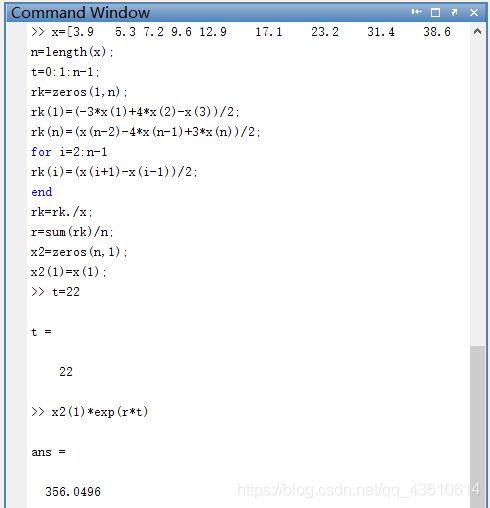
对2010年人口预测
已经求得r与x0代码:
x=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76 92 105.7 122.8 131.7 150.7 179.3 203.2 226.5 248.7 281.4];
n=length(x);
t=0:1:n-1;
rk=zeros(1,n);
rk(1)=(-3*x(1)+4*x(2)-x(3))/2;
rk(n)=(x(n-2)-4*x(n-1)+3*x(n))/2;
for i=2:n-1
rk(i)=(x(i+1)-x(i-1))/2;
end
rk=rk./x;
r=sum(rk)/n;
x2=zeros(n,1);
x2(1)=x(1);
>> t=22;
>> x2(1)*exp(r*t)
改进的指数增长模型
指数增长模型进行改进。改进为:
假设:
![]()
![]()
利用dsolve()函数可得:
![]()
已知t值,根据上面我们已经求过了rk,所以rk也是已知的,然后利用最小二乘法polyfit()函数计算出![]()
中的r0和r1,x0=3.9,利用eval()函数求出结果
运行代码:
函数:
function [ x3 ] =method_3( x )
%方法三:改进的指数增长模型
% Detailed explanation goes here
n=length(x);
t=0:1:n-1;
rk=zeros(1,n);
rk(1)=(-3*x(1)+4*x(2)-x(3))/2;
rk(n)=(x(n-2)-4*x(n-1)+3*x(n))/2;
for i=2:n-1
rk(i)=(x(i+1)-x(i-1))/2;
end
rk=rk./x;
p=polyfit(t,rk,1);
r0=p(2);
r1=-p(1);
s=dsolve('Dx=(r0-r1*t)*x','x(0)=x0','t');
x0=3.9;
x3=zeros(n,1);
x3=eval(s);
x3=x3';
end
运行代码:
x=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76 92 105.7 122.8 131.7 150.7 179.3 203.2 226.5 248.7 281.4];
m=1790:10:2000;
m=m';
m(:,2)=x';
m(:,3)=method_1(x);
m(:,4)=method_2(x);
m(:,5)=method_3(x);
运行界面:
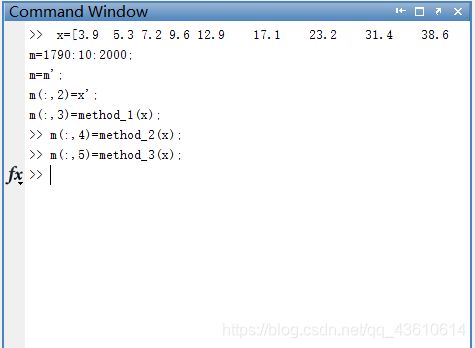
运行结果:第一列代表年份;第二列代表实际人口;第三列为指数增长模型:方法一的预估值;第四列为指数增长模型:方法二的预估值;第五列改进指数模型的预估值

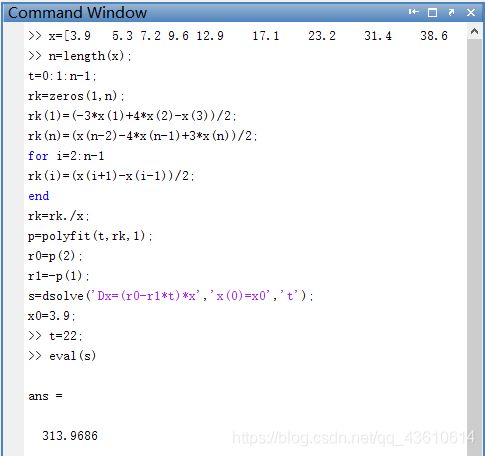
对2010人口预测
>> x=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76 92 105.7 122.8 131.7 150.7 179.3 203.2 226.5 248.7 281.4];
>> n=length(x);
t=0:1:n-1;
rk=zeros(1,n);
rk(1)=(-3*x(1)+4*x(2)-x(3))/2;
rk(n)=(x(n-2)-4*x(n-1)+3*x(n))/2;
for i=2:n-1
rk(i)=(x(i+1)-x(i-1))/2;
end
rk=rk./x;
p=polyfit(t,rk,1);
r0=p(2);
r1=-p(1);
s=dsolve('Dx=(r0-r1*t)*x','x(0)=x0','t');
x0=3.9;
>> t=22;
>> eval(s)
逻辑斯蒂(logistic)模型
xm:表示人口容量
有了人口容量的限制,当人口数量增加时,增长率r减小,用![]()
表示。
逻辑斯蒂(logistic)模型:方法一
function [ x4 ] = logistic_1( x )
%逻辑斯蒂模型方法一
n=length(x);
t=0:1:n-1;
rk=zeros(1,n);
rk(1)=(-3*x(1)+4*x(2)-x(3))/2;
rk(n)=(x(n-2)-4*x(n-1)+3*x(n))/2;
for i=2:n-1
rk(i)=(x(i+1)-x(i-1))/2;
end
rk=rk./x;
p=polyfit(x,rk,1);
b=p(1);
a=p(2);
r=a;
xm=-r/b;
s=dsolve('Dx=r*x*(1-x/xm)','x(0)=x0','t');
x0=3.9;
x4=eval(s);
x4=x4';
x4=abs(x4);
end
运行代码:
x=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76 92 105.7 122.8 131.7 150.7 179.3 203.2 226.5 248.7 281.4];
m=1790:10:2000;
m=m';
m(:,2)=x';
m(:,3)=method_1(x);
m(:,4)=method_2(x);
m(:,5)=method_3(x);
m(:,6)=logistic_1(x);
运行界面:
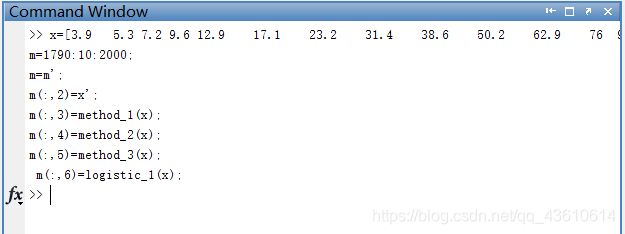
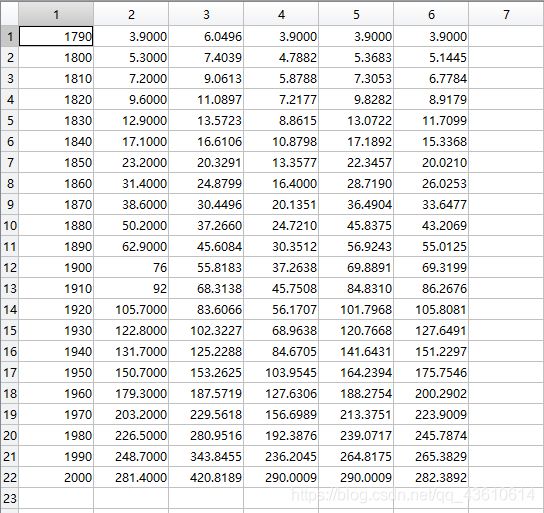
运行结果:第一列代表年份;第二列代表实际人口;第三列为指数增长模型:方法一的预估值;第四列为指数增长模型:方法二的预估值;第五列改进指数模型的预估值;第六列逻辑斯蒂方法一预估值
对2010预测
代码:
>> x=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76 92 105.7 122.8 131.7 150.7 179.3 203.2 226.5 248.7 281.4];
>> n=length(x);
t=0:1:n-1;
rk=zeros(1,n);
rk(1)=(-3*x(1)+4*x(2)-x(3))/2;
rk(n)=(x(n-2)-4*x(n-1)+3*x(n))/2;
for i=2:n-1
rk(i)=(x(i+1)-x(i-1))/2;
end
rk=rk./x;
p=polyfit(x,rk,1);
b=p(1);
a=p(2);
r=a;
xm=-r/b;
s=dsolve('Dx=r*x*(1-x/xm)','x(0)=x0','t');
x0=3.9;
>> t=22;
>> eval(s)
逻辑斯蒂(logistic)模型:方法二
直接用数据和非线性最小而成估计参数:
运行代码:
function [ x5 ] = logistic_2( x )
%逻辑斯蒂模型方法二
n=length(x);
t=0:1:n-1;
f=@(a,t)a(1)./(1+(a(1)./a(2)-1).*exp(-a(3).*t));
[A,cancha]=lsqcurvefit(f,[500,3.9,0.3],t,x);
s=dsolve('Dx=r*x*(1-x/xm)','x(0)=x0','t');
r=A(3);
x0=A(2);
xm=A(1);
x5=eval(s);
x5=x5';
x5=abs(x5);
end
运行代码:
x=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76 92 105.7 122.8 131.7 150.7 179.3 203.2 226.5 248.7 281.4];
m=1790:10:2000;
m=m';
m(:,2)=x';
m(:,3)=method_1(x);
m(:,4)=method_2(x);
m(:,5)=method_3(x);
m(:,6)=logistic_1(x);
m(:,7)=logistic_2(x);
运行界面:
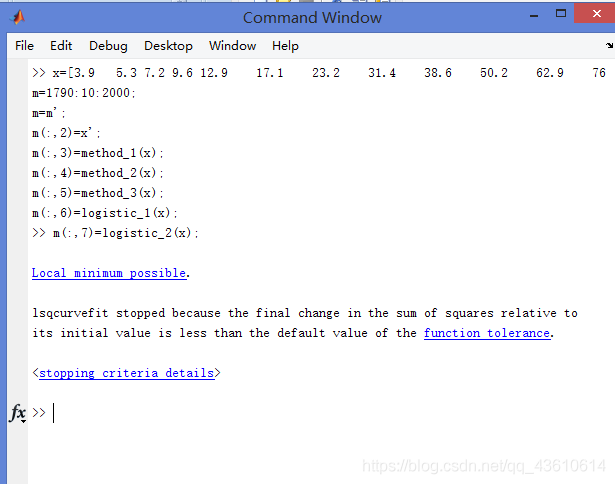
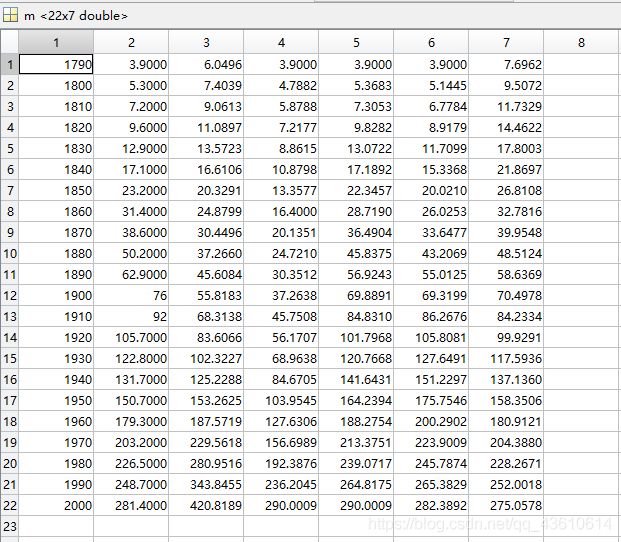
运行结果:第一列代表年份;第二列代表实际人口;第三列为指数增长模型:方法一的预估值;第四列为指数增长模型:方法二的预估值;第五列改进指数模型的预估值;第六列逻辑斯蒂方法一预估值;第七列逻辑斯蒂方法二预估值
对2010预测
代码:
x=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76 92 105.7 122.8 131.7 150.7 179.3 203.2 226.5 248.7 281.4];
>> n=length(x);
t=0:1:n-1;
f=@(a,t)a(1)./(1+(a(1)./a(2)-1).*exp(-a(3).*t));
[A,cancha]=lsqcurvefit(f,[500,3.9,0.3],t,x);
s=dsolve('Dx=r*x*(1-x/xm)','x(0)=x0','t');
r=A(3);
x0=A(2);
xm=A(1);
>> t=22;
>> eval(s)