淦VINS-MONO源码 03--openCV与VINS中去畸变方法的不同
openCV与VINS中去畸变方法的不同
- 畸变
-
- 畸变参数和去畸变公式
-
- 径向畸变:
- 切向畸变
- 畸变模型
- openCV去畸变函数
-
- cv::undistortPoints()
-
- 源码
- VINS-MONO去畸变函数
-
- liftProjective()
- 源码
畸变
透镜由于制造精度以及组装工艺的偏差会引入畸变,导致原始图像的失真。镜头的畸变分为径向畸变和切向畸变两类。
畸变参数和去畸变公式
径向畸变:
顾名思义,径向畸变就是沿着透镜半径方向分布的畸变,产生原因是光线在原理透镜中心的地方比靠近中心的地方更加弯曲,这种畸变在短焦镜头中表现更加明显,径向畸变主要包括桶形畸变和枕形畸变两种。以下分别是枕形和桶形畸变示意图:

成像仪光轴中心的畸变为0,沿着镜头半径方向向边缘移动,畸变越来越严重。畸变的数学模型可以用主点(principle point)周围的泰勒级数展开式的前几项进行描述,通常使用前两项,即k1和k2,对于畸变很大的镜头,如鱼眼镜头,可以增加使用第三项k3来进行描述,成像仪上某点根据其在径向方向上的分布位置,调节公式为:
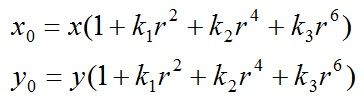
下图是距离光心不同距离上的点经过透镜径向畸变后点位的偏移示意图,可以看到,距离光心越远,径向位移越大,表示畸变也越大,在光心附近,几乎没有偏移。
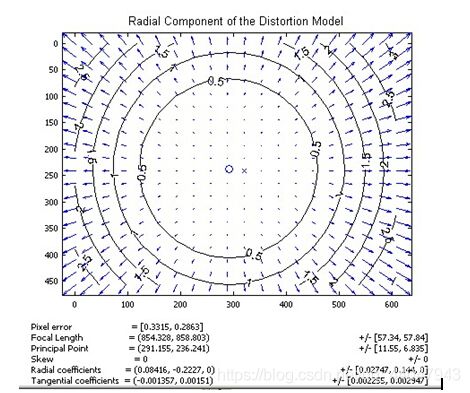
切向畸变
切向畸变是由于透镜本身与相机传感器平面(成像平面)或图像平面不平行而产生的,这种情况多是由于透镜被粘贴到镜头模组上的安装偏差导致。

畸变模型可以用两个额外的参数p1和p2来描述:
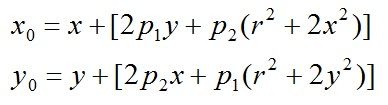
下图显示某个透镜的切向畸变示意图,大体上畸变位移相对于左下——右上角的连线是对称的,说明该镜头在垂直于该方向上有一个旋转角度。

畸变模型
同时对径向、切向畸变消除就是将两组式子合并。
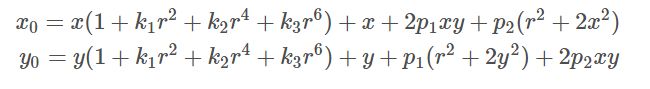
然后坐标变换过程这里就简单说一下:

畸变模型对应的是归一化平面的坐标,但我们已知的是畸变后的图像坐标(u,v),那么就要把(u,v)变换会归一化平面再反向求出正常位置坐标,再求出真实的(u,v),但是去畸变函数的反向是个非线性化问题,难以求解,下面我们就看看openCV和VINS-MONO是怎么处理的:
openCV去畸变函数
在opencv中,有关图像或像素点(角点)去畸变的函数有cv::undistort(),cv::getOptimalNewCameraMatrix(),cv::initUndistortRectifyMap(),remap(),cv::undistortPoints()。其中undistort可以直接对图像去畸变。undistortPointsS是对坐标点去畸变。
如果你比较关心怎么调用这些API,我推荐阅读这篇文章: 关于OpenCV中的去畸变.这篇文章介绍了每个函数的参数,以及各个函数的不同。
下面我将从源码层面以undistortPoints()为例和VINS-MONO的distortion()方法进行对比,看看vins-mono用了一个巧妙的办法,来加速去畸变过程。
cv::undistortPoints()
opencv中函数undistortPoints()用于对图像点坐标进行去畸变,以下为该函数解释:
void undistortPoints(InputArray src, OutputArray dst, InputArray cameraMatrix,
InputArray distCoeffs, InputArray R=noArray(), InputArray P=noArray())
src-原图像坐标;dst-输出图像坐标;cameraMatrix-相机内参矩阵;distCoeffs-畸变系数,有四种畸变模型,分别含有4,5,8个元素,通常使用具有4/5个参数的模型,如果该向量为NULL,那么设定该图像没有畸变;R-相机坐标系的矫正矩阵(即对相机坐标系的位姿调整,见stereoRectify函数中的Rl,Rr),如果矩阵为空,那么默认使用单位矩阵;P-新的相机矩阵(3x3)或者新的投影矩阵(3x4,包含相机坐标系相对世界坐标系的相对位姿,见stereoRectify函数中的Pl,Pr),如该矩阵为空的话,将设置该矩阵为单位阵。
源码
void cvUndistortPointsInternal( const CvMat* _src, CvMat* _dst, const CvMat* _cameraMatrix,
const CvMat* _distCoeffs,
const CvMat* matR, const CvMat* matP, cv::TermCriteria criteria)
{
// 判断迭代条件是否有效
CV_Assert(criteria.isValid());
// 定义中间变量--A相机内参数组,和matA共享内存;RR-矫正变换数组,和_RR共享内存
// k-畸变系数数组
double A[3][3], RR[3][3], k[14]={0,0,0,0,0,0,0,0,0,0,0,0,0,0};
CvMat matA=cvMat(3, 3, CV_64F, A), _Dk;
CvMat _RR=cvMat(3, 3, CV_64F, RR);
cv::Matx33d invMatTilt = cv::Matx33d::eye();
cv::Matx33d matTilt = cv::Matx33d::eye();
// 检查输入变量是否有效
CV_Assert( CV_IS_MAT(_src) && CV_IS_MAT(_dst) &&
(_src->rows == 1 || _src->cols == 1) &&
(_dst->rows == 1 || _dst->cols == 1) &&
_src->cols + _src->rows - 1 == _dst->rows + _dst->cols - 1 &&
(CV_MAT_TYPE(_src->type) == CV_32FC2 || CV_MAT_TYPE(_src->type) == CV_64FC2) &&
(CV_MAT_TYPE(_dst->type) == CV_32FC2 || CV_MAT_TYPE(_dst->type) == CV_64FC2));
CV_Assert( CV_IS_MAT(_cameraMatrix) &&
_cameraMatrix->rows == 3 && _cameraMatrix->cols == 3 );
cvConvert( _cameraMatrix, &matA );// _cameraMatrix <--> matA / A
// 判断输入的畸变系数是否有效
if( _distCoeffs )
{
CV_Assert( CV_IS_MAT(_distCoeffs) &&
(_distCoeffs->rows == 1 || _distCoeffs->cols == 1) &&
(_distCoeffs->rows*_distCoeffs->cols == 4 ||
_distCoeffs->rows*_distCoeffs->cols == 5 ||
_distCoeffs->rows*_distCoeffs->cols == 8 ||
_distCoeffs->rows*_distCoeffs->cols == 12 ||
_distCoeffs->rows*_distCoeffs->cols == 14));
_Dk = cvMat( _distCoeffs->rows, _distCoeffs->cols,
CV_MAKETYPE(CV_64F,CV_MAT_CN(_distCoeffs->type)), k);// _Dk和数组k共享内存指针
cvConvert( _distCoeffs, &_Dk );
if (k[12] != 0 || k[13] != 0)
{
cv::detail::computeTiltProjectionMatrix<double>(k[12], k[13], NULL, NULL, NULL, &invMatTilt);
cv::detail::computeTiltProjectionMatrix<double>(k[12], k[13], &matTilt, NULL, NULL);
}
}
if( matR )
{
CV_Assert( CV_IS_MAT(matR) && matR->rows == 3 && matR->cols == 3 );
cvConvert( matR, &_RR );// matR和_RR共享内存指针
}
else
cvSetIdentity(&_RR);
if( matP )
{
double PP[3][3];
CvMat _P3x3, _PP=cvMat(3, 3, CV_64F, PP);
CV_Assert( CV_IS_MAT(matP) && matP->rows == 3 && (matP->cols == 3 || matP->cols == 4));
cvConvert( cvGetCols(matP, &_P3x3, 0, 3), &_PP );// _PP和数组PP共享内存指针
cvMatMul( &_PP, &_RR, &_RR );// _RR=_PP*_RR 放在一起计算比较高效
}
const CvPoint2D32f* srcf = (const CvPoint2D32f*)_src->data.ptr;
const CvPoint2D64f* srcd = (const CvPoint2D64f*)_src->data.ptr;
CvPoint2D32f* dstf = (CvPoint2D32f*)_dst->data.ptr;
CvPoint2D64f* dstd = (CvPoint2D64f*)_dst->data.ptr;
int stype = CV_MAT_TYPE(_src->type);
int dtype = CV_MAT_TYPE(_dst->type);
int sstep = _src->rows == 1 ? 1 : _src->step/CV_ELEM_SIZE(stype);
int dstep = _dst->rows == 1 ? 1 : _dst->step/CV_ELEM_SIZE(dtype);
double fx = A[0][0];
double fy = A[1][1];
double ifx = 1./fx;
double ify = 1./fy;
double cx = A[0][2];
double cy = A[1][2];
int n = _src->rows + _src->cols - 1;
// 开始对所有点开始遍历
for( int i = 0; i < n; i++ )
{
double x, y, x0 = 0, y0 = 0, u, v;
if( stype == CV_32FC2 )
{
x = srcf[i*sstep].x;
y = srcf[i*sstep].y;
}
else
{
x = srcd[i*sstep].x;
y = srcd[i*sstep].y;
}
u = x; v = y;
x = (x - cx)*ifx;//转换到归一化图像坐标系(含有畸变)
y = (y - cy)*ify;
//进行畸变矫正
if( _distCoeffs ) {
// compensate tilt distortion--该部分系数用来弥补沙氏镜头畸变??
// 如果不懂也没管,因为普通镜头中没有这些畸变系数
cv::Vec3d vecUntilt = invMatTilt * cv::Vec3d(x, y, 1);
double invProj = vecUntilt(2) ? 1./vecUntilt(2) : 1;
x0 = x = invProj * vecUntilt(0);
y0 = y = invProj * vecUntilt(1);
double error = std::numeric_limits<double>::max();// error设定为系统最大值
// compensate distortion iteratively
// 迭代去除镜头畸变
// 迭代公式 x′= (x−2p1 xy−p2 (r^2 + 2x^2))∕( 1 + k1*r^2 + k2*r^4 + k3*r^6)
// y′= (y−2p2 xy−p1 (r^2 + 2y^2))∕( 1 + k1*r^2 + k2*r^4 + k3*r^6)
for( int j = 0; ; j++ )
{
if ((criteria.type & cv::TermCriteria::COUNT) && j >= criteria.maxCount)// 迭代最大次数为5次
break;
if ((criteria.type & cv::TermCriteria::EPS) && error < criteria.epsilon)// 迭代误差阈值为0.01
break;
double r2 = x*x + y*y;
double icdist = (1 + ((k[7]*r2 + k[6])*r2 + k[5])*r2)/(1 + ((k[4]*r2 + k[1])*r2 + k[0])*r2);
double deltaX = 2*k[2]*x*y + k[3]*(r2 + 2*x*x)+ k[8]*r2+k[9]*r2*r2;
double deltaY = k[2]*(r2 + 2*y*y) + 2*k[3]*x*y+ k[10]*r2+k[11]*r2*r2;
x = (x0 - deltaX)*icdist;
y = (y0 - deltaY)*icdist;
// 对当前迭代的坐标加畸变,计算误差error用于判断迭代条件
if(criteria.type & cv::TermCriteria::EPS)
{
double r4, r6, a1, a2, a3, cdist, icdist2;
double xd, yd, xd0, yd0;
cv::Vec3d vecTilt;
r2 = x*x + y*y;
r4 = r2*r2;
r6 = r4*r2;
a1 = 2*x*y;
a2 = r2 + 2*x*x;
a3 = r2 + 2*y*y;
cdist = 1 + k[0]*r2 + k[1]*r4 + k[4]*r6;
icdist2 = 1./(1 + k[5]*r2 + k[6]*r4 + k[7]*r6);
xd0 = x*cdist*icdist2 + k[2]*a1 + k[3]*a2 + k[8]*r2+k[9]*r4;
yd0 = y*cdist*icdist2 + k[2]*a3 + k[3]*a1 + k[10]*r2+k[11]*r4;
vecTilt = matTilt*cv::Vec3d(xd0, yd0, 1);
invProj = vecTilt(2) ? 1./vecTilt(2) : 1;
xd = invProj * vecTilt(0);
yd = invProj * vecTilt(1);
double x_proj = xd*fx + cx;
double y_proj = yd*fy + cy;
error = sqrt( pow(x_proj - u, 2) + pow(y_proj - v, 2) );
}
}
}
// 将坐标从归一化图像坐标系转换到成像平面坐标系
double xx = RR[0][0]*x + RR[0][1]*y + RR[0][2];
double yy = RR[1][0]*x + RR[1][1]*y + RR[1][2];
double ww = 1./(RR[2][0]*x + RR[2][1]*y + RR[2][2]);
x = xx*ww;
y = yy*ww;
if( dtype == CV_32FC2 )
{
dstf[i*dstep].x = (float)x;
dstf[i*dstep].y = (float)y;
}
else
{
dstd[i*dstep].x = x;
dstd[i*dstep].y = y;
}
}
}
可以看到比较关键的就是 通过通过公式反向求解进行迭代(优化问题),然后对当前迭代的坐标加畸变,计算误差error用于判断迭代条件。
VINS-MONO去畸变函数
VINS中去除畸变的方法就非常巧妙了,刚看懂的时候大呼牛X。
首先我们知道越靠近中心,畸变前后的距离差越小。那么我们可以用这个关系来逼近真值求解问题。我们先来看代码:
liftProjective()
源码
void PinholeCamera::liftProjective(const Eigen::Vector2d& p, Eigen::Vector3d& P) const
{
double mx_d, my_d,mx2_d, mxy_d, my2_d, mx_u, my_u;
double rho2_d, rho4_d, radDist_d, Dx_d, Dy_d, inv_denom_d;
//double lambda;
// Lift points to normalised plane
// 投影到归一化相机坐标系
mx_d = m_inv_K11 * p(0) + m_inv_K13;
my_d = m_inv_K22 * p(1) + m_inv_K23;
if (m_noDistortion)
{
mx_u = mx_d;
my_u = my_d;
}
else
{
if (0)
{
double k1 = mParameters.k1();
double k2 = mParameters.k2();
double p1 = mParameters.p1();
double p2 = mParameters.p2();
// Apply inverse distortion model
// proposed by Heikkila
mx2_d = mx_d*mx_d;
my2_d = my_d*my_d;
mxy_d = mx_d*my_d;
rho2_d = mx2_d+my2_d;
rho4_d = rho2_d*rho2_d;
radDist_d = k1*rho2_d+k2*rho4_d;
Dx_d = mx_d*radDist_d + p2*(rho2_d+2*mx2_d) + 2*p1*mxy_d;
Dy_d = my_d*radDist_d + p1*(rho2_d+2*my2_d) + 2*p2*mxy_d;
inv_denom_d = 1/(1+4*k1*rho2_d+6*k2*rho4_d+8*p1*my_d+8*p2*mx_d);
mx_u = mx_d - inv_denom_d*Dx_d;
my_u = my_d - inv_denom_d*Dy_d;
}
else
// 参考https://github.com/HKUST-Aerial-Robotics/VINS-Mono/issues/48
{
// Recursive distortion model
int n = 8;
Eigen::Vector2d d_u;
// 这里mx_d + du = 畸变后
distortion(Eigen::Vector2d(mx_d, my_d), d_u);
// Approximate value
mx_u = mx_d - d_u(0);
my_u = my_d - d_u(1);
for (int i = 1; i < n; ++i)
{
distortion(Eigen::Vector2d(mx_u, my_u), d_u);
mx_u = mx_d - d_u(0);
my_u = my_d - d_u(1);
}
}
}
// Obtain a projective ray
P << mx_u, my_u, 1.0;
}
这里用的方法和openCV不同,假设现在求A点的去畸变坐标,那么我们将A的坐标直接代入畸变模型中,求得再次畸变的坐标,并求得这个坐标和A之间的距离d.因为越靠近中心这个d越小,此时肯定小于真实坐标到A的距离dt。所以我们在朝真实畸变方向(再次畸变的反方向)上加上这个d,得到一个靠近真实值的方向,在以这个点再进行一次畸变求得距离d2,d2肯定大于d小于dt。d2在加到坐标A上 得到更靠近的结果,代码中一共进行了8次迭代。这种方法比openCV中的方法快了不少。