【量化交易笔记】8.基于深度学习(LSTM)预测股票价格
前言
前一章节,已作随机森林来预测股票价格,也是一种比较常见的方法,本章基于深度学习算法来处理时间序列,来预测股票未来的价格。LSTM是一种特殊类型的循环神经网络(RNN),在自然语言处理和时间序列数据分析等任务中取得了显著成果。LSTM通过处理序列数据中的长期依赖关系,能够更好地捕捉时间序列数据的特征和模式。这使得它成为预测股票价格这类时间相关数据的有力工具。关于LSTM 在之前的文章中也略作介绍。
我们仍以上一章的数据,采用类似于上一章的处理方式进行处理。
获取数据
本章我们采用 tensorflow框架的keras 来实现LSTM。
# 加载相应的库
import numpy as np
import pandas as pd
import tensorflow as tf
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus']=False
from keras.models import Sequential
from keras.layers import Dense ,LSTM, Dropout
from sklearn.preprocessing import MinMaxScaler
%matplotlib inline
这部分内容,仍以sh.60000为例,从2019年1月1日 到至今天(2023-5-31)。
# 加载数据
df=pd.read_csv("data/sh.600000.csv",parse_dates=["date"],index_col=[0])
df.head()
| date | code | open | high | low | close | preclose | volume | amount | adjustflag | turn | tradestatus | pctChg | isST |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2019-01-02 | sh.600000 | 8.079311 | 8.120785 | 7.946591 | 8.046131 | 8.129080 | 23762822 | 229625669.0 | 2 | 0.084554 | 1 | -1.020412 | 0 |
| 2019-01-03 | sh.600000 | 8.046131 | 8.145670 | 8.012951 | 8.137375 | 8.046131 | 18654262 | 181975985.0 | 2 | 0.066376 | 1 | 1.134027 | 0 |
| 2019-01-04 | sh.600000 | 8.071016 | 8.294980 | 8.046131 | 8.261800 | 8.137375 | 27172844 | 268964563.0 | 2 | 0.096688 | 1 | 1.529048 | 0 |
| 2019-01-07 | sh.600000 | 8.369635 | 8.369635 | 8.228620 | 8.278390 | 8.261800 | 23597376 | 235440197.0 | 2 | 0.083965 | 1 | 0.200798 | 0 |
| 2019-01-08 | sh.600000 | 8.319865 | 8.319865 | 8.220325 | 8.261800 | 8.278390 | 15104933 | 150501650.0 | 2 | 0.053747 | 1 | -0.200396 | 0 |
分离数据
由于是时间序列,特征选 'open','high','low','close','volume','turn',考虑到volume得范围比较大,而股票价格,换手率比较小,采用MinMaxScaler对数据进行归一化处理,进行统一缩放到相同大小。
cols=['open','high','low','close','volume','turn']
df=df[cols]
scaler = MinMaxScaler(feature_range=(0,1))
df_scaled = scaler.fit_transform(df)
数据集处理
我们想用前30天数据预测第二天收盘价,这里的30天,即所有数据,由于LSTM 模型的特殊性,采用createXY函数生成数据。
具体这个函数
def createXY(dataset,n_past):
j=0
dataX = []
dataY = []
for i in range(n_past, len(dataset)):
x=dataset[i - n_past:i, 0:dataset.shape[1]]
if (i+n_past>=len(dataset)):
y=0
else:
y=dataset[i-1+n_past,3]
dataX.append(x)
dataY.append(y)
return np.array(dataX),np.array(dataY)
dataX,dataY=createXY(df_scaled,30)
让我们看看上面的代码中做了什么:
n_past是我们在预测下一个目标值时将在过去查看的步骤数。
这里使用30,意味着将使用过去的30个值(包括目标列在内的所有特性)来预测第31个目标值。
因此,在trainX中我们会有所有的特征值,而在trainY中我们只有目标值。
让我们分解for循环的每一部分
对于训练,dataset = df_for_training_scaled, n_past=30
当i= 30:
data_X.addend (df_for_training_scaled[i - n_past:i, 0:df_for_training.shape[1]])
从n_past开始的范围是30,所以第一次数据范围将是-[30 - 30,30,0:6] 相当于 [0:30,0:6]
因此在dataX列表中,df_for_training_scaled[0:30,0:6]数组将第一次出现。
现在, dataY.append(df_for_training_scaled[i,3])
i = 30,所以它将只取第30行开始的close(因为在预测中,我们只需要close列,所以列范围仅为3,表示close列)。
第一次在dataY列表中存储df_for_training_scaled[30,3]值。
所以包含5列的前30行存储在dataX中,只有close列的第31行存储在dataY中。然后我们将dataX和dataY列表转换为数组,它们以数组格式在LSTM中进行训练。
将数据集拆分为训练集、验证集和测试集。由于这个数据集是时间序列,以2023年前的数据作为训练集,之后数据为验证集。
npreddata_X=dataX[-30:]
npreddata_Y=dataY[-30:]
ddf_X=dataX[:-30]
ddf_Y=dataY[:-30]
test_split=68 #这里是从2023-1-1开始计时
trainX=ddf_X[:-test_split]
trainY=ddf_Y[:-test_split]
testX=ddf_X[-test_split:]
testY=ddf_Y[-test_split:]
看一下数据结构
trainX.shape,trainY.shape,testX.shape,testY.shape
((942, 30, 6), (942,), (68, 30, 6), (68,))
看到这里大家有没有看明白了,如果还不明白,我再给大伙解释一下
如果查看 trainX[1] 值,会发现到它与 trainX[0] 中的数据相同(第一列除外),因为我们将看到前 30 个来预测第 31 列,在第一次预测之后它会自动移动 到第 2 列并取下一个 30 值来预测下一个目标值。
让我们用一种简单的格式来解释这一切——
trainX — — →trainY
[0 : 30,0:6] → [30,3]
[1:31, 0:6] → [31,3]
[2:32,0:6] →[32,3]
这下应该看明白了。
建模
以一般的 LSTM 模式,用Adam优化器,用mse作为损失函数,采用二层结构进行建模。
grid_model = Sequential()
grid_model.add(LSTM(50,return_sequences=True,input_shape=(30,6)))
grid_model.add(LSTM(50))
grid_model.add(Dropout(0.2))
grid_model.add(Dense(1))
grid_model.compile(loss = 'mse',optimizer = 'adam')
grid_model.summary()
Model: "sequential_4"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
lstm_8 (LSTM) (None, 30, 50) 11400
lstm_9 (LSTM) (None, 50) 20200
dropout_4 (Dropout) (None, 50) 0
dense_4 (Dense) (None, 1) 51
=================================================================
Total params: 31,651
Trainable params: 31,651
Non-trainable params: 0
_________________________________________________________________
训练
这里用 batch_size 用16 ,epochs =40来进行训练,在实际情况一下,数据集的数据量大的话,机器内存在或采用GPU等,可以用更大的参数,epoch 也可以有更大的参数。
history=grid_model.fit(
trainX, trainY,
batch_size = 16,
epochs =40,
validation_data=(testX,testY)
)
_________________________________________________________________
Output exceeds the size limit. Open the full output data in a text editor
Epoch 1/40
59/59 [==============================] - 1s 21ms/step - loss: 0.0088 - val_loss: 0.0030
Epoch 2/40
59/59 [==============================] - 1s 22ms/step - loss: 0.0089 - val_loss: 0.0036
Epoch 3/40
59/59 [==============================] - 2s 26ms/step - loss: 0.0084 - val_loss: 0.0099
Epoch 4/40
59/59 [==============================] - 1s 19ms/step - loss: 0.0082 - val_loss: 0.0129
Epoch 5/40
59/59 [==============================] - 1s 18ms/step - loss: 0.0079 - val_loss: 0.0059
Epoch 6/40
59/59 [==============================] - 1s 19ms/step - loss: 0.0078 - val_loss: 0.0061
Epoch 7/40
59/59 [==============================] - 1s 20ms/step - loss: 0.0078 - val_loss: 0.0051
Epoch 8/40
59/59 [==============================] - 1s 19ms/step - loss: 0.0075 - val_loss: 0.0113
Epoch 9/40
59/59 [==============================] - 1s 19ms/step - loss: 0.0074 - val_loss: 0.0075
Epoch 10/40
59/59 [==============================] - 1s 22ms/step - loss: 0.0070 - val_loss: 0.0045
Epoch 11/40
59/59 [==============================] - 1s 20ms/step - loss: 0.0078 - val_loss: 0.0088
Epoch 12/40
59/59 [==============================] - 1s 20ms/step - loss: 0.0073 - val_loss: 0.0090
Epoch 13/40
...
Epoch 39/40
59/59 [==============================] - 1s 19ms/step - loss: 0.0041 - val_loss: 0.0058
Epoch 40/40
59/59 [==============================] - 1s 19ms/step - loss: 0.0038 - val_loss: 0.0056
由于训练数据和测试数据是经过归一化的,因此要查看结果,需要将数据逆缩放过程。
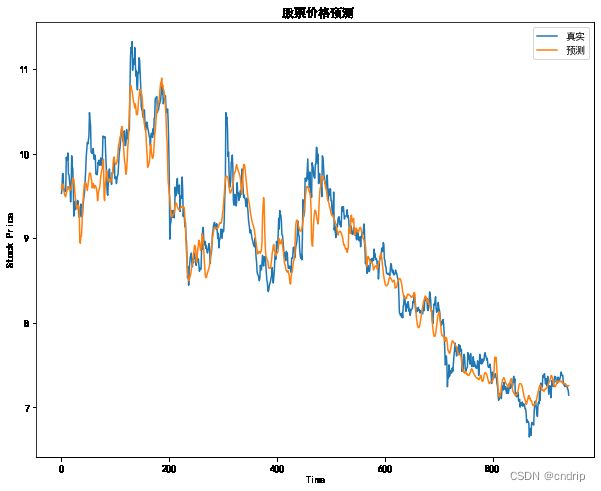
先看训练集数据。
tprediction=grid_model.predict(trainX)
tprediction_copies_array = np.repeat(tprediction,6, axis=-1)
tpred=scaler.inverse_transform(np.reshape(tprediction_copies_array,(len(tprediction),6)))[:,0]
toriginal_copies_array = np.repeat(trainY,6, axis=-1)
toriginal=scaler.inverse_transform(np.reshape(toriginal_copies_array,(len(trainY),6)))[:,0]
plt.figure(figsize=(10, 8))
plt.plot(toriginal, label = '真实')
plt.plot(tpred, label = '预测')
plt.title(' 股票价格预测')
plt.xlabel('Time')
plt.ylabel('Stock Price')
plt.legend()
plt.show()
prediction=grid_model.predict(testX)
prediction_copies_array = np.repeat(prediction,6, axis=-1)
pred=scaler.inverse_transform(np.reshape(prediction_copies_array,(len(prediction),6)))[:,0]
original_copies_array = np.repeat(testY,6, axis=-1)
# original_copies_array.shape
original=scaler.inverse_transform(np.reshape(original_copies_array,(len(testY),6)))[:,0]
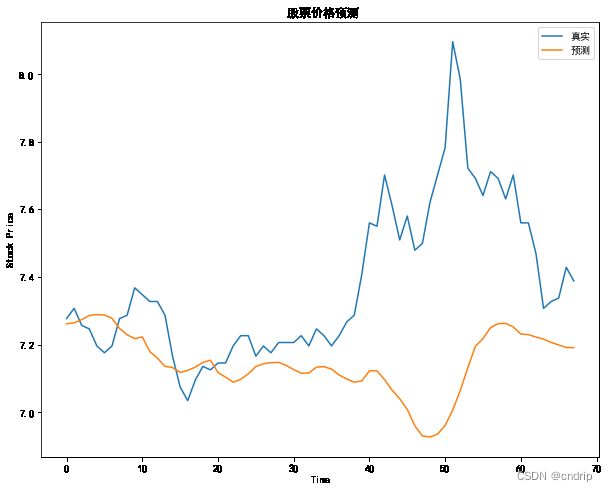
plt.figure(figsize=(10, 8))
plt.plot(original, label = '真实')
plt.plot(pred, label = '预测')
plt.title(' 股票价格预测')
plt.xlabel('Time')
plt.ylabel('Stock Price')
plt.legend()
plt.show()
评估
from sklearn.metrics import make_scorer,mean_squared_error,mean_absolute_error
print('MSE:',mean_squared_error(toriginal,tpred),mean_squared_error(original,pred))
print('MAE:',mean_absolute_error(toriginal,tpred),mean_absolute_error(original,pred))
MSE: 0.05473229063101591 0.12244576326985654
MAE: 0.17944593014201451 0.24734961573477243
从MSE和 MAE来看,值并不大。从数值上看并不大,可从图形上来看预测效果并不理想。
作图
见上图
总结
以上是深度学习中RNN中的LSTM来作股票价格预测,从结果来看效果并不理想,作为一种方法,需要我们掌握的。除了LSTM之外,还有GAN和ANN等方法,处理数据方面大同小异,GAN 是一种比较特殊的方法。
由于在实际应用中效果不理解,很少被采用,因此不作过多的介绍。
总之,我们学习其方法以及原理,决不能作为投资的依据。
以后可以通过机器学习来生成投资策略,那还是比较靠谱的。那是机器学习的另一个应用。
在此警告:文章中的所有内容,不能给你构成投资的理由。