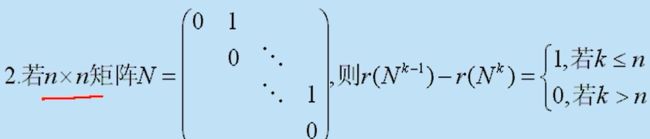【矩阵论】矩阵的相似标准型（4）(5)

矩阵的相似标准型之Jordan标准形

这一节视频的开头，对于线性变换对角化的定理3的证明与例题的内容，我放在上一篇文章的最后了。

如果是同步着视频来看文章的读者可以查看上一篇文章《【矩阵论】矩阵的相似标准型（3）》

前面我们花了很多篇幅来讨论，如果一个矩阵可以对角化，那么判定对角化的条件是什么，可对角化又会有哪些方便计算和求解性质的相关定理。

但问题在于，矩阵可对角化需要较为严苛的条件。

因此，对于不能对角化的矩阵A，我们希望找到一个形式更加简单的矩阵B，A相似于B，通过矩阵B来简化一些计算。

• 从矩阵的角度来思考，计算更加明确
• 从线性变换的角度来思考，更利于建立直观印象
  【强调】这里问题可以建立等价关系，是因为“同一线性变换在不同基下表示的矩阵是相似的”，这个定理在之前的课程中介绍并证明过！！

---

一. Jordan形矩阵

1. 定义

（1）Jordan块

Jordan块是一个上三角矩阵，其主对角线上元素均相等，为a；主对角线上面的一条斜线上的元素均为1；其余元素均为0。

特殊地，当k = 1时，一阶Jordan块是[a]。

（2）Jordan形矩阵

Jordan形矩阵是一个分块对角矩阵，其中每一个小分块都是一个Jordan块。

Tip 1：整体来看Jordan形矩阵，其主对角线上的所有元素并不一定是相同的，只要求每一个分块的主对角线元素分别相同即可。
Tip 2：因为Jordan块可以是一阶的，如果每一个Jordan块都是一阶的，构成的Jordan形矩阵就是一个对角矩阵。对角矩阵是特殊的Jordan形矩阵。

（3）标准形

若矩阵A与Jordan形矩阵J相似，则称J是A的标准形。

因为对角阵是特殊的Jordan形矩阵，所以之前讨论过的对角化问题——某一矩阵A相似于一个对角阵Λ，也可以说Λ矩阵就是A的标准形。

由此，对角化问题其实是标准形问题的一个特例。

---

【例】判断矩阵是否为Jordan形矩阵

读者可以先自行判断，答案见下方

对于正确的Jordan形矩阵，用黑线给出了分块形式；对于错误的Jordan形矩阵，给出了需要更改的元素。

---

2. 存在性和唯一性

前面已经讨论了Jordan形矩阵的定义，现在需要进一步讨论，对于每一个矩阵，其相应的Jordan标准形是否唯一。

一般情况下，每一个矩阵的Jordan标准形是唯一的，但这个唯一性成立是需要条件的。

（1）对矩阵A的Jordan标准形中的每个分块阵改变排列顺序，得到的依然是Jordan标准形

【证明】
要证明一个矩阵是A的Jordan标准形——其一，该矩阵符合Jordan标准形的定义；其二，矩阵A也相似于这个矩阵。
毋庸置疑，改变各个分块的排列顺序得到的依然是符合Jordan标准形定义的；
现在需要证明A也相似于K矩阵。

[1]：按照题目已知，J是A的Jordan标准形，就说明J和A相似；对相似变换矩阵P进行列分块，转换相似等式。

p.s. 在矩阵对角化中这一招也屡试不爽呀~

[2]：按照分块矩阵的运算规则，得到了AP_ij =P_ijJ_ij，其中j = 1,2,…s。

p.s. 对矩阵P进行分块的时候，要配合矩阵J中各个分块的维度来，这样才能正确进行分块矩阵的乘法运算。

[3]：按照K中给出的排列方式，相对应地组织出一个新的相似变换矩阵Q，因为P是可逆的，且Q相对于P只是进行了一些初等变换，所以Q也是可逆矩阵。进行A·Q的运算，因为之前得到的一系列等式AP_ij =P_ijJ_ij，所以可以得到AQ = QK。

故而，证明出矩阵A也是相似于矩阵K的。

通过以上证明和结论，我们所讨论的唯一性，是在排除了Jordan形各个分块的顺序之后再考虑的。

也就是说，不考虑各个分块阵的顺序变化，一个矩阵A的Jordan标准形往往是唯一的。

（2）Jordan形矩阵的唯一性证明

①证明依据

a. 矩阵与其Jordan标准形在秩上的关系

证明过程直接看下图，又是利用矩阵相似的优良性质的一天~

b. 一个特殊矩阵及其秩的递推关系

对于上图矩阵N，其幂乘运算结果很有特点：每和自己做一次乘法，全1元素的斜线就会向右上方平移一行。
形如：


根据矩阵元素的分布特点，也可以得到——r(Nⁱ) = max(0,n-i)；其中n是方阵N的维数

p.s. 当约定了N⁰ = I时，上述秩的关系式对于k = 1也是同样适用的。

c. 这个标题我总结不出来了

【证明】
既然结论和“以λ₀为主对角元的Jordan块的块数”相关，那么可以把J设成以下形式：


其中，J₀表示的是以λ₀作为主对角线元素的Jordan块集合；K表示的是其他元素作为主对角线元素的Jordan块集合。

按照题目中给出的形式，作形如(J-λ₀I)^k的矩阵多项式运算，因为J是分块矩阵，得到的结果就是各个分块阵分别作出相应多项式运算。

分块对角矩阵还具有良好的性质——整个矩阵的秩等于各个分块矩阵的秩之和。
因此：把题目中要求的r(J-λ₀I)^k-1-r(J-λ₀I)^k记作#式，即#= r(J-λ₀I)^k-1-r(J-λ₀I)^k

按照分块对角矩阵秩的特点，则有：
因为矩阵K是所有主对角线元素都不是λ₀的Jordan矩阵，因此K-λ₀I一定是一个可逆矩阵，那么其不论进行多少阶的幂乘运算，结果依然是一个可逆矩阵（因为K也是分块对角的）。

如果设r(K) = r₀，则r(K-λ₀I)^k = r(K-λ₀I)^k-1 = r₀，所以这两项可以相互抵消。
因此#式子的值就有了改变，# = r(J₀-λ₀I)^k-1-r(J₀-λ₀I)^k

再来看(J₀-λ₀I)，因为其主对角线上元素都是λ₀，因此(J₀-λ₀I)^k是下图形式的分块对角矩阵：

其中每一个N_j矩阵，都是主对角元素全为0，主对角线右上方一条斜线位置全为1的矩阵，与结论b中的矩阵N是一致的。

按照分块对角矩阵的秩的性质：
可以得到 # = (r(N₁)^k-1-r(N₁)^k)+(r(N₂)^k-1-r(N₂)^k)+…+r(N_t)^k-1-r(N_t)^k
根据结论b的性质，每一个括号里两者之差取决于运算的阶次k和矩阵本身的阶数n之间的关系，如果阶数n≥k，那么每两项的差就应该是1，否则就是0，因此可以得到——题目中所求的两项秩之差就是J中阶数≥k的，以λ₀为主对角元的Jordan块的块数。

根据结论c，如果我们想要求解Jordan矩阵中以λ₀为主对角线元素，且阶数就是k的Jordan块的块数 ——用阶数≥k的块数减去阶数≥k-1的块数即可，代入结论，即有：

②定理

如果认真看完了上述结论c的证明以及推论描述的话，这一定理的证明思路是完全相同的，但同时也要请读者注意该定理和上述结论c的文字描述略有不同，以下描述：

• 结论c中中是用Jordan形矩阵J参与多项式运算，r(J-λ₀I)；但是在本定理中是用元矩阵A参与多项式运算，r(A-λ₀I)
  原因：矩阵A和该矩阵的Jordan矩阵J是相似的，所以其矩阵多项式的秩也是相等的。
  
• 结论c中的λ₀是Jordan形矩阵J的一个主对角线上的元素，但是该定理中λ₀是原矩阵A的一个特征值。
  原因：既然A和J是相似的，那么A与J具有相同的特征值，J又是一个上三角形矩阵（Jordan形矩阵的定义），所以Jordan形矩阵对角线的元素就是J矩阵的特征值，也就是矩阵A的特征值。

意义：根据这个定理，我们只要针对矩阵A的每一个特征值λ₀，依次求解相应于这个特征值的每一阶Jordan块的块数，就可以把矩阵A的Jordan矩阵完全求解出来。

但实际上，这一工作需要太大的计算量，在实际中不会采用。我们只需要明确，根据一个矩阵A的特征值、A-λI、阶数k等信息就能够完全确定矩阵A相对应的Jordan块矩阵即可。

---

【例】-1 求解矩阵的Jordan标准形

根据题目给出的已知条件是无法完全确定一个矩阵的Jordan标准形的，所以我们需要求解出所有可能满足条件的Jordan标准形。

【题型框架】
不给出矩阵A的具体形式，只根据相关特征信息，选出可能的Jordan形矩阵。

由矩阵A的特征多项式可以知道矩阵A是6阶方阵，且A的Jordan形矩阵的主对角线上的元素有2个1和4个2，形如以下。

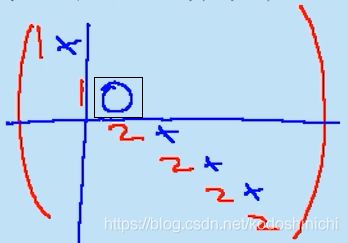
上图中，因为以1为主对角元的分块矩阵和以2为主对角元的分块矩阵肯定不在一个Jordan块中，所以可以确定上图黑框处为元素0；但我们仍然需要确定“x”处的元素是0还是1.

因为r(A-2I) = 4,我们所需求解的矩阵J和矩阵A又是相似的，所以也应该有r(J-2I) = 4.
矩阵J的形式如上图所示，将所有的对角线元素都减去一个2之后，左上方的分块对角阵可以贡献出2的秩，那么就要求右下的分块矩阵也要贡献出4-2 = 2的秩；因为右下方矩阵的对角线元素减去2之后全为零，所以次对角线上的三个“x”需要有两个1，一个0.

则右下分块矩阵可能的形式有以下两种：

不知道会不会有读者跟我一样稍微疑惑了一下，三个“x”，排两个1一个0，应该有3中全排列，怎么会只有两种可能呢？

因为：“0”排在最下面和“0”排在最上面其实是等价的。我们需要比较的并不是不同的排列方式的个数，而是划分的Jordan块的个数。

“0”排在最上面和最下面，得到的都是一个3阶的以2为主对角元的Jordan块和一个1阶的以2为主对角元的Jordan块；而“0”在中间对应的就是两个以2为主对角元的Jordan块。

之前我们讨论过了，我们所讨论的Jordan标准形的唯一性，是基于不计Jordan块的排列顺序而言的。所以相同的Jordan块调换顺序，我们视作同样的Jordan标准形。

当然最后有四种可能的Jordan矩阵，因为最左上方的"x"元素，根据题目给出的有限已知条件是无法确定的，所以取0取1均可以，一共有2x2种可能的Jordan形矩阵。

---

【例】 -2 求解矩阵的Jordan标准形

【题型框架】
给出了矩阵A的完整形式，要求根据矩阵挖掘出相关信息，求解其Jordan形矩阵的唯一形式。

根据求出来的特征多项式C_A，1是A的三重特征值，可以得出A的Jordan形矩阵只可能在以下三种形式中求解。

（1）验证条件1：A与J相似
如果J = I（第一种可能性），那么存在一个可逆矩阵P，使得P^-1AP = J = I也就是AP = P，即A = I，与题意明显不符，故排除第一种可能性。

（2）验证条件2：计算矩阵多项式的秩
记第二种和第三种可能的Jordan形矩阵为J₂和J₃,那么计算可得r(J₂-I) = 1;r(J₃-I) = 2.
因为矩阵A相似于J，所以有r(A-I) = r(J-I),通过计算r(A-I) = 1，可知道最终的Jordan形矩阵就是J₂。

---

二. Jordan标准形与分块矩阵的最小多项式

在上一部分中，我们是通过矩阵的秩来证明出矩阵的Jordan标准形的唯一性，以及通过求解矩阵多项式的秩来确定针对某一特征值，某一阶数的Jordan块的个数来确定矩阵的Jordan矩阵的维数。

但有的时候，我们还需要确定矩阵的Jordan标准形和它的最小多项式之间的关系。

1. 定理：分块对角阵各个分块的最小多项式间的关系

（1）定理描述

分块对角阵的最小多项式是各个分块的最小多项式的“首一”（最高阶因式系数为1）的最小多项式的最小公倍数。

（2）定理证明

设d(λ) = [m_A(λ)，m_B(λ)]，也就是A与B两个矩阵的最小多项式的最小公倍数（首一的），按照题意，需要证明m_M(λ)和d(λ)相等，因为两个关于λ的多项式都是首一的，故只需要证明两个多项式可以互相整除，就可以说明两个多项式是相等的。

m_M(λ)是M的最小多项式，按照前面的定义，我们知道任意一个矩阵的化零多项式都可以被其最小多项式整除，

于是乎，我们大胆推测，如果d(λ)就是矩阵的化零多项式，那么就可以整除d(λ)能被m_M(λ)整除。

a. d(λ)能被m_M(λ)整除
按照最小公倍数的定义，可设d(λ)分别是m_A(λ)和m_B(λ)的f(λ)和g(λ)倍：

既然要证明d(λ)是矩阵M的化零多项式，那么就要把矩阵M代入多项式看最终结果是否为零矩阵。

【分块对角矩阵的多项式运算】

前面我们已经关于“分块对角矩阵”总结了很多优良性质，比如关于矩阵的秩，矩阵的行列式，矩阵的特征值等等…
分块对角矩阵的多项式(含幂乘)运算也具有很优秀的性质。

假设M是一个形如[[A,O],[O,B]]这样的分块对角阵，其的幂乘运算就是对各个分块子矩阵进行幂乘运算，其多项式运算也就是对各个分块子矩阵进行多项式运算。

因此，按照上图的运算，分别将矩阵A和B代入d(λ)中，因为d(λ)同时含有A和B矩阵最小多项式的因子，最小多项式也是化零多项式，得到的结果就是一个零矩阵。

说明——d(λ)的确是矩阵M的化零多项式。也就是说m_M(λ)可以整除d(λ)。

b. m_M(λ)能被d(λ)整除
因为m_M(λ)是矩阵M的最小多项式，按照定义，将矩阵M代入到多项式中，并且结合分块对角矩阵的运算规律，可以得到[[m_M(A),O],[O,m_M(B)]]矩阵是一个零矩阵。

按照上图，那就说明各个分块都应该是零矩阵，从而得出m_M(A) = m_M(B) = O。
按照化零多项式的定义，上面的两个等式就说明了m_M(λ)既是矩阵A的化零多项式，也是矩阵B的化零多项式。

设矩阵A和B的最小多项式分别为m_A(λ)和m_B(λ)，则可以得到m_M(λ)既能被m_A(λ)整除，也能被m_B(λ)整除，所以m_M(λ)可以被m_A(λ)和m_B(λ)的最小公倍数（也就是d(λ)）整除。

综上，即证明了m_M(λ)和d(λ)的相互整除，也就是d(λ) = m_M(λ)，说明分块对角阵的最小多项式就是各个分块的最小多项式的最小多项式的最小公倍数。

---

2. Jordan标准形与最小多项式的关系

（1）定理描述

其中λ_i（i=1,2,…,s）是互异的。
此定理说明A的Jordan标准形中以某一特征值为主对角线元的Jordan块的最高阶数就是特征值在最小多项式中的重数。

（2）定理证明
设矩阵A的Jordan形矩阵为J，那么可知A与J相似，因为J矩阵在不考虑各个Jordan块的时候是唯一的，我们可以人为把矩阵J的形式整理成以下：

其中每个J_i都是以λ_i为主对角元的Jordan形矩阵。
（注意，这里是划分成了各个小的Jordan形矩阵，每个Jordan形矩阵含有若干Jordan块）
对于每个J_i矩阵，含有t_i个Jordan块，每个Jordan块的主对角元也是特征值λ_i。

我们知道矩阵A和矩阵J具有相同的最小多项式，由第一个定理，矩阵J的最小多项式应该是所有J_i矩阵的最小多项式的最小公倍数。
问题转变为求各J_i矩阵的最小多项式。

矩阵J_i中每个Jordan块K_i的形式如下图所示

而Jordan块K_i的最小多项式形如右式，是因子(λ-λ_i)的某阶多项式，m_Ki = （λ-λ_i）^?
根据前面学过的定理，我们可以确定这个“?”就是K_iJordan块的阶数。

因为最小多项式也是化零多项式，所以m_Ki(K_i) = (K_i-λ_iI)^? = O。

将上图中的K_i矩阵的对角线元素全部减去λ_i，得到的就是N矩阵
N矩阵的某一幂次运算结果要为零矩阵，根据我们之前的证明，这个“？”至少也得是矩阵的阶数。

而根据最小多项式中“最低”次数的要求，“？”不能超过矩阵的维数.

所以最后可知m_Ki(λ) = (λ-λ_i)^dim(Ki)

因为每一个J_i矩阵也是一个关于K_i的分块对角矩阵，依然利用定理一：

只不过因为每个m_Ki(λ)都只含有(λ-λ_i)这个因子，只是幂次dim(K_i)不同而已，所以M_Ji(λ) = (λ-λ_i)^max·dim(Ki)

这里的max dim(K_i)的含义也就是以λ_i为主对角线元的Jordan块的最高阶数。

解决完每个J_i的最小多项式后，我们再回到最终需要解决的J矩阵的最小多项式的问题上来。

因为m_Ji(λ)所含的因式都不一样（λ_i是互异的），所以m_J(λ)就是把各个m_Ji(λ)直接相乘即可。

将这个式子和题目给出的m(x)的形式相对照，证毕。

（3）推论

特别地，当A相似于对角阵 ↔ A的最小多项式无重根。

因为此时A的Jordan标准形（也就是这个对角阵）中每一个Jordan块都是一阶的，每一个因子的幂次也就是1。

---

【例】- 1 由矩阵的特征、最小多项式确定可能的Jordan形

<解>
首先由矩阵的特征多项式，可以确定Jordan形主对角线上的元素个数和数值，如下：

根据最小多项式，可知道以1为主对角元的矩阵最高阶只有1阶；以2为主对角元的Jordan块最高阶为2阶。
故只可能有以下两种形式：

【自我小结-脑洞】
p.s. 笔者自己的总结，语言描述可能比较意识流，读者可以跳过它。

之前通过秩来确定次对角线上的元素是0还是1的时候，我们往往碰到的问题是“一共有n个元素，应该要有m个1,n-m个0”；那时，笔者特意提醒，可能的结果并不是A(n,m)全排列的所有情况，因为我们需要确定的是不同的Jordan块的划分可能，全排列中会有重复的情况。

但是现在我们得到的信息直接就是各个Jordan块的阶数，比如有5个2，我们知道最高阶只能是2，那么只可能是“1个2,3个1”或者是“2个2,1个1”，这样思考出来的结果就已经是最终的情况了，因为我们是直接针对Jordan块的划分来讨论的，不会存在重复的情况了。
p.s. 当然这里的问题是组合问题，不考虑顺序。

---

【例】- 2 由矩阵的特征、最小多项式确定可能的Jordan形

<解>
a. A的Jordan形
根据特征多项式可知道主对角元是4个0，根据最小多项式可知道Jordan形矩阵中只含有一个4阶的Jordan块。

b. A²的Jordan形

【思维扫盲】
可能我们会按照A与J相似的思路，联想到那么A²和J²也是相似的，从而认为J²就是A²的Jordan形。

当然这个思路是经不起推敲的，比如在这一题中将J²算出来明显不符合Jordan形矩阵的形式。


但同时，它为我们提供了一个新的思路，既然A²与J²相似，那么A²的Jordan形就是J²的Jordan形，我们可以利用J²这个较为具体的矩阵来求解标准形。

因为J²是上三角矩阵，对角线元素只有2，说明其标准形的主对角元也只有零元素，且J²的秩为2，说明次对角线的3个空位中应该有两个1，可能是以下两种情况。

如果对J²进行平方运算，结果是零矩阵，通过这一点可以验证第二个矩阵才是J²（也就是A²）的标准形。

老师在验证平方运算的结果是不是零矩阵的时候，又十分巧妙地用了N矩阵的结论。

按照下图的分块——
第一个矩阵的左上分块是3阶N矩阵，进行2次幂乘运算结果还有一个1，非零矩阵；
第二个矩阵的两个分块都是2阶的N矩阵，进行2次幂乘运算结果都变成零矩阵。