论文笔记--Prompt Consistency for Zero-Shot Task Generalization
论文笔记--Prompt Consistency for Zero-Shot Task Generalization
- 1. 文章简介
- 2. 文章概括
- 3 文章重点技术
-
- 3.1 Prompt-based zero-shot task generalization
- 3.2 Prompt Consistency Training
- 3.3 如何防止遗忘和退化?
- 4. 文章亮点
- 5. 原文传送门
1. 文章简介
- 标题:Prompt Consistency for Zero-Shot Task Generalization
- 作者:Chunting Zhou, Junxian He, Xuezhe Ma, Taylor Berg-Kirkpatrick, Graham Neubig
- 日期:2022
- 期刊:Arxiv preprint
2. 文章概括
文章基于prompt的一致性学习给出了一种zero-shot task generalization(零样本泛化学习)的无监督方法。数值实验表明,文章提出的指令一致性学习方法只需在几个prompt、几十个样本上进行训练,就可以在NLI等NLP任务上追平SOTA水平。
文章整体架构如下
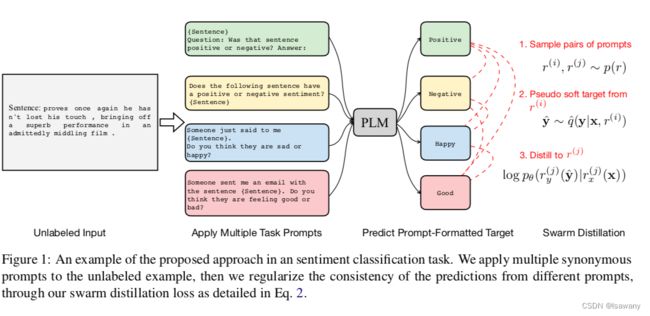
3 文章重点技术
3.1 Prompt-based zero-shot task generalization
首先简单介绍下zero-shot task generalization(零样本泛化学习):给定输入 x ∈ X x\in \mathcal{X} x∈X,零样本泛化学习旨在学习一个预训练模型PLM预测出 y ∈ Y y\in \mathcal{Y} y∈Y,其中PLM未在数据集 X \mathcal{X} X上训练过。零样本泛化学习要求模型可以泛化出一个新的表达式 f : X → Y f: \mathcal{X} \to \mathcal{Y} f:X→Y,而非仅仅在数据集上具有泛化能力。
给定prompt r r r, r r r包含一个输入模板 r x r_x rx、输出模板 r y r_y ry以及待放入模板的元数据 x , y x, y x,y,我们可以得到prompt-based输入: r x ( x ) , r y ( y ) r_x(x), r_y(y) rx(x),ry(y)。基于prompt的学习方法一般用 p θ ( r y ( y ) ∣ r x ( x ) ) p_{\theta} (r_y(y)|r_x(x)) pθ(ry(y)∣rx(x))来计算输出的概率 q ( y ∣ x , r ) ) q(y|x, r)) q(y∣x,r)),其中 θ \theta θ表示模型的参数。本文重点关注NLP的分类任务,则可以通过如下公式计算输出的概率: q ( y ∣ x , r ) = p θ ( r y ( y ) ∣ r x ( x ) ) ∑ y ′ ∈ Y p θ ( r y ( y ′ ) ∣ r x ( x ) ) (1) q(y|x, r) = \frac{p_{\theta} (r_y(y)|r_x(x))}{\sum_{y'\in\mathcal{Y}} p_{\theta} (r_y(y')|r_x(x))}\tag{1} q(y∣x,r)=∑y′∈Ypθ(ry(y′)∣rx(x))pθ(ry(y)∣rx(x))(1)。
3.2 Prompt Consistency Training
文章的方法需要无标注的数据集 { x 1 , … , x N } \{x_1, \dots, x_N\} {x1,…,xN}和 K K K个不同的prompt { ( r x 1 , r y 1 ) , … , ( r x K , r y K ) } \{(r_x^1, r_y^1), \dots, (r_x^K, r_y^K)\} {(rx1,ry1),…,(rxK,ryK)}。其中无标注的数据集可以来自任意NLP(分类)任务的训练数据集或测试数据集,也可以来自我们要测试的任务的数据集。prompt可直接采用Public Pool of Prompts(p3)数据集里的prompt。
传统的一致性训练会扰乱样本,使得扰乱后的样本和之前的样本得到的输出尽可能一致。本文希望学习prompt级别的一致性,即不同prompt在单个样本上的学习结构尽可能一致。这样做可以1) 概念非常简单 2)缓解PLM“输入不同prompt结果不一致”的问题。
损失函数定义如下 L = − E x ∈ p d ( x ) E r i , e r j ∈ p ( r ) E y ^ ∈ q ^ ( y ∣ x , r i ) log p θ ( r y j ( y ^ ) ∣ r x j ( x ) ) \mathcal{L} = -\mathbb{E}_{x\in p_d(x)} \mathbb{E}_{r^i, er^j\in p(r)} \mathbb{E}_{\hat{y} \in \hat{q}(y|x,r^i)} \log p_{\theta} (r_y^j(\hat{y})|r_x^j(x)) L=−Ex∈pd(x)Eri,erj∈p(r)Ey^∈q^(y∣x,ri)logpθ(ryj(y^)∣rxj(x))
, p d p_d pd是数据集的分布, p ( r ) p(r) p(r)表示 K K K个prompt的随机prompt对的均匀分布, q ^ \hat{q} q^定义为式(1)的条件分布。这里简单解释下,如图所示,给定prompt r i , r j r^i, r^j ri,rj,我们首先预测 y ^ ∈ q ^ ( y ∣ x , r i ) \hat{y}\in \hat{q}(y|x, r^i) y^∈q^(y∣x,ri),即当promt为 r i r^i ri时得到输出 y ^ \hat{y} y^。当prompt为 r j r^j rj时,我们希望最大化输出结果为 y ^ \hat{y} y^(即和 r i r^i ri输出相同)的概率 p θ ( r y j ( y ^ ) ∣ r x j ( x ) ) p_{\theta} (r_y^j(\hat{y})|r_x^j(x)) pθ(ryj(y^)∣rxj(x)),取负对数和期望之后,即得到上述损失函数。我们称上述训练方法为swarm distillation。
3.3 如何防止遗忘和退化?
如果直接采用上述方法进行训练,则我们很容易collapse,得到一个平凡解:所有prompt、所有样本均输出同一个结果可以实现损失函数最小。另一方面,训练后的模型可以能忘记之前的知识,即castrophic forgetting。为了避免collapse和catastrophic forgetting,文章提出下述两种方法:
- LoRA:文章是在T0模型上层进行训练的,为了不发生灾难性遗忘,文章采用了LoRA方法,即通过两个低阶矩阵的乘积进行迭代学习,具体如下图所示。在实际训练时我们将LoRA应用到Transformer每一个前馈层。
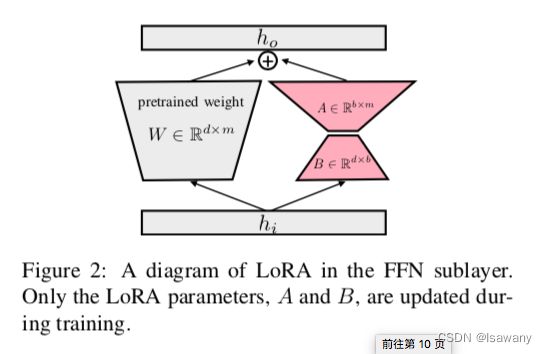
- Fleiss’ Kappa:由于我们没有标注数据作为validation set,从而很难选择一个最佳的checkpoint作为最终模型。为此文章采用了Fleiss’ Kappa指标来度量模型的效果。首先,我们定义一致性概率。对给定的样本 x i x_i xi,记所有 K K K个prompt中预测输出为第 j j j个label的prompt数量为 n i j n_{ij} nij,则对该样本,任意两个prompt给出相同的预测结果的概率为 p i = ∑ j ( n i j 2 ) / ( K 2 ) = ∑ j n i j ( n i j − 1 ) / K ( K − 1 ) p_i = \sum_j \binom {n_{ij}}2 /\binom K2 = \sum_{j} n_{ij}(n_{ij} - 1) / K(K-1) pi=j∑(2nij)/(2K)=j∑nij(nij−1)/K(K−1),所有样本的绝对一致性为 P ‾ = ∑ i p i \overline{P} = \sum_i p_i P=∑ipi。另一方面,第 j j j个label的占比为 q j = ∑ i n i j / N K q_j = \sum_i n_{ij}/NK qj=∑inij/NK,则 P ‾ e = ∑ j q j 2 \overline{P}_e = \sum_j q_j^2 Pe=∑jqj2表示任意两个prompts按照标签的分布随机预测结果一致的概率。当所有 q j q_j qj均相等时, P ‾ e \overline{P}_e Pe最小,即预测的标签随机分布。最终得到Fleiss’ kappa度量为 κ = P ‾ − P ‾ e 1 − P ‾ e ∈ ( − 1 , 1 ) \kappa = \frac {\overline{P} - \overline{P}_e}{1 - \overline{P}_e} \in (-1, 1) κ=1−PeP−Pe∈(−1,1),其中 P ‾ e \overline{P}_e Pe越大, κ \kappa κ越小,即预测的结果如果被一个类别主导,则 κ \kappa κ会被惩罚。
4. 文章亮点
文章提出了一种基于prompt一致性的zero-shot task generation学习方法swarm distillation,且采用了LoRA和Fleiss’ Kappa方法避免学习灾难性遗忘或学习结果collapse。文章在多个NLP下游任务上进行了验证,发现swarm distillation在多个任务上表现超过SOTA。此外,数值实验表明,swarm distillation只需要4个prompt,10+个样本就可以对源模型(T0)进行提升。
但实验也表明,swarm distillation方法在增加到一定样本量之后性能就达到了饱和,当我们有很多标记样本可用的时候,性能可能不及监督微调。未来可以将swarm distillation与few-shot少样本学习或预训练相结合来实现在标记样本上的性能提升。
5. 原文传送门
Prompt Consistency for Zero-Shot Task Generalization