结构之美——优先队列基本结构(四)——二叉堆、d堆、左式堆、斜堆
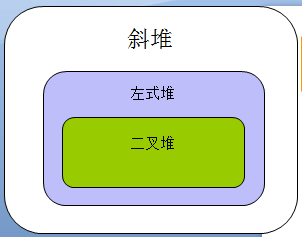
实现优先队列结构主要是通过堆完成,主要有:二叉堆、d堆、左式堆、斜堆、二项堆、斐波那契堆、pairing 堆等。
1. 二叉堆
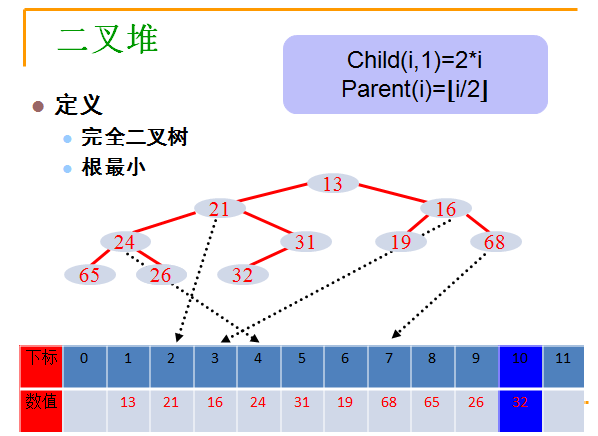
1.1. 定义
完全二叉树,根最小。
存储时使用层序。
1.2. 操作
(1). insert(上滤)
插入末尾 26,不断向上比较,大于26则交换位置,小于则停止。
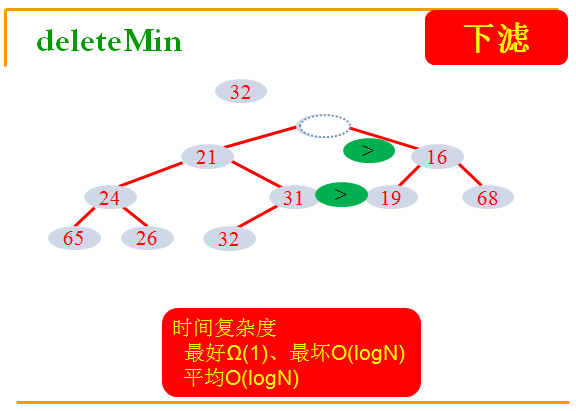
(2). deleteMin(下滤)
提取末尾元素,放在堆顶,不断下滤:
(3). 其他操作:
都是基于insert(上滤)与deleteMin(下滤)的操作。
减小元素:减小节点的值,上滤调整堆。
增大元素:增加节点的值,下滤调整堆。
删除非顶点节点:直接删除会出问题。方法:减小元素的值到无穷小,上滤后删除。
Merge:insert one by one
2. d叉堆
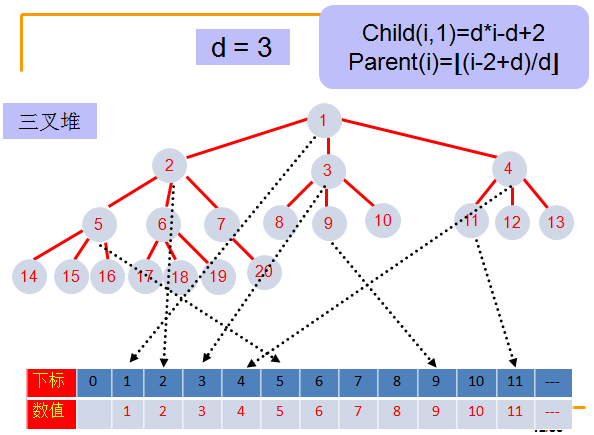
2.1. 定义
完全d叉树,根最小。
存储时使用层序。
2.2. 操作:
操作跟二叉堆基本一致:insert,deleteMin,增大元素,减小元素,删除非顶元素,merge。
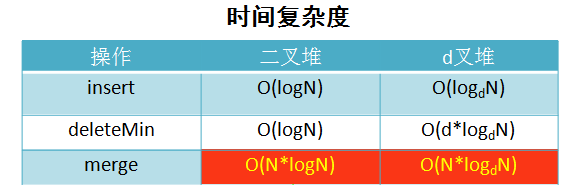
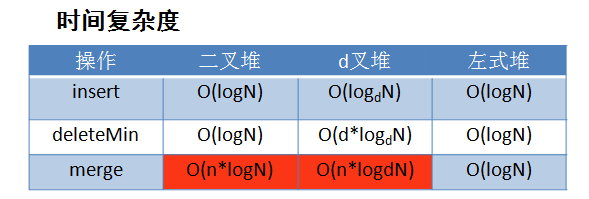
2.3 二叉堆与d叉堆的对比:
3. 左式堆
3.1. 定义
3.2. 操作:
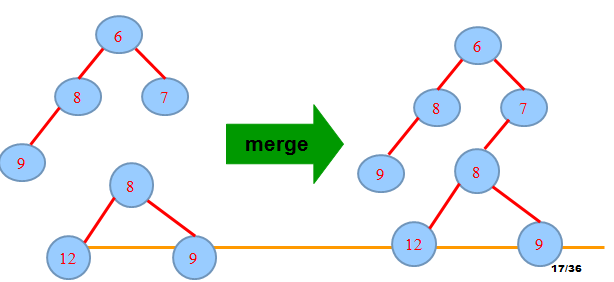
(1) merge :
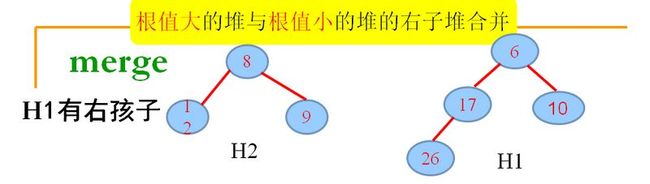
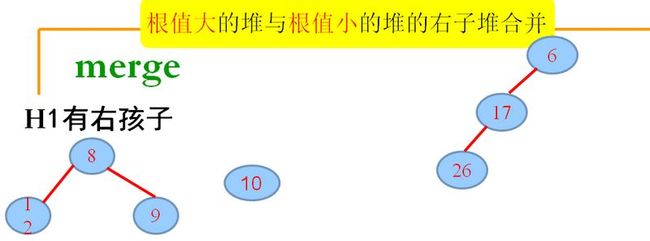
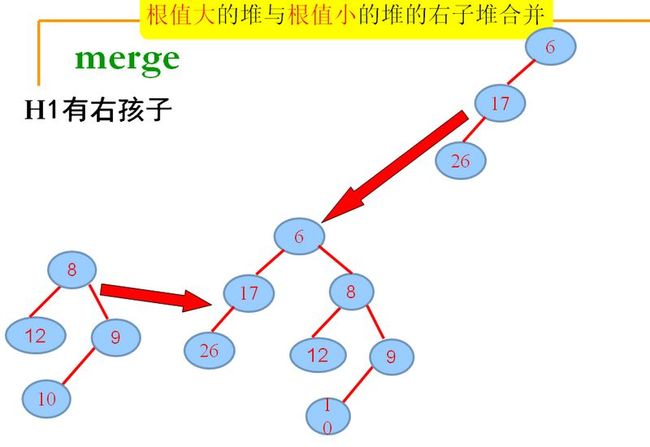
(1.3).H1根有右孩子
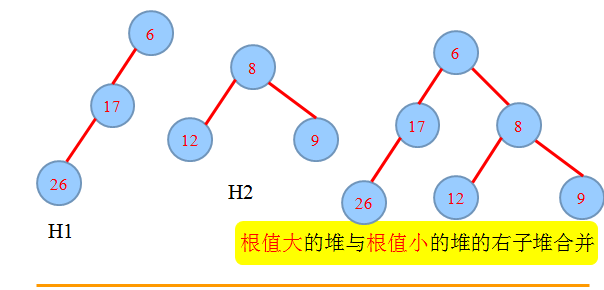
1.初始状态,H1的根6,H2的根为8,将H2合并到H1。
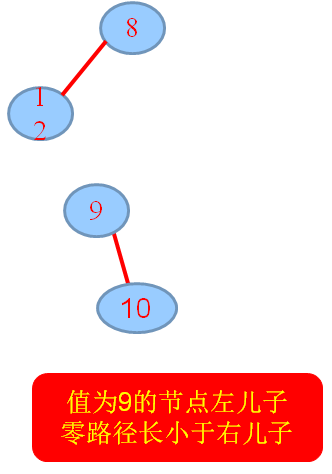
2.将H1构造成根无右孩子的形式:
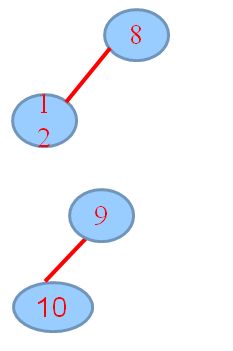
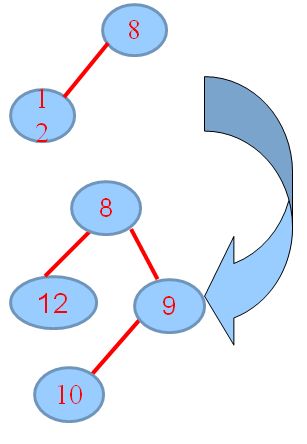
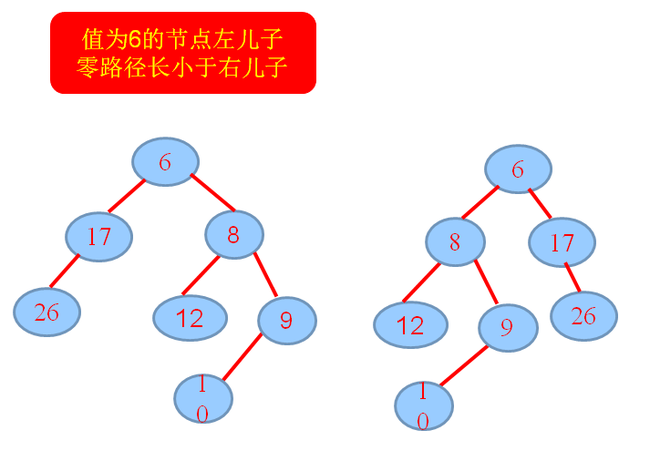
3.将元素10, merge到H2,要首先将H2构造成根无右孩子的形式,递归,merge,若出现不满足:零路径长:左儿子≧右儿子,交换左右孩子……
4.
5.
3.3. 性质分析:
4. 斜堆
4.1. 定义
4.2性能比较:
定義
- 僅有一個節點的樹為斜堆;
- 兩個斜堆合併的結果仍為斜堆。
合併操作
斜堆合併操作的遞歸合併過程和左偏樹完全一樣。假設我們要合併 A 和 B兩個斜堆,且 A 的根節點比 B 的根節點小,我們只需要把 A 的根節點作為合併後新斜堆的根節點,並將 A 的右子樹與 B 合併。由於合併都是沿著最右路徑進行的,經過合併之後,新斜堆的最右路徑長度必然增加,這會影響下一次合併的效率。所以合併後,通過交換左右子樹,使整棵樹的最右路徑長度非常小(這是啟發規則)。然而斜堆不記錄節點的距離,在操作時,從下往上,沿著合併的路徑,在每個節點處都交換左右子樹。通過不斷交換左右子樹,斜堆把最右路徑甩向左邊了。
遞歸實現合併
- 比較兩個堆; 設p是具有更小的root的鍵值的堆,q是另一個堆,r是合併後的結果堆。
- 令r的root是p(具有最小root鍵值),r的右子樹為p的左子樹。
- 令r的左子樹為p的右子樹與q合併的結果。
非遞歸合併實現
- 把每個堆的每棵(遞歸意義下)最右子樹切下來。這使得得到的每棵樹的右子樹均為空。
- 按root的鍵值的升序排列這些樹。
- 迭代合併具有最大root鍵值的兩棵樹:
- 具有次大root鍵值的樹的右子樹必定為空。把其左子樹與右子樹交換。現在該樹的左子樹為空。
- 具有最大root鍵值的樹作為具有次大root鍵值樹的左子樹。
5. 总结
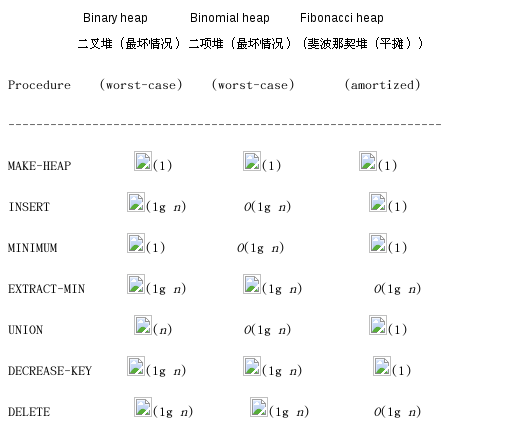
如果是不支持所谓的合并操作union的话,普通的堆数据结构就是一种很理想的数据结构(堆排序)。 但是如果想要支持集合上的合并操作的话,最好是使用二项堆或者是斐波那契堆,普通的堆在union操作上最差的情况是O(n),但是二项堆和斐波那契堆是O(lgn)。