第七章 集成学习
文章目录
- 第七章 集成学习
-
- 7.1个体和集成
- 7.2Boosting和AdaBoost
- 7.3Bagging和随机森林
-
- 7.3.1Bagging
- 7.3.2随机森林
- 7.4结合策略
-
- 7.4.1平均法
- 7.4.2投票法
- 7.4.3学习法
- 7.6实验:Adaboost
第七章 集成学习
7.1个体和集成
集成学习通过构建并结合多个学习器来完成学习任务,有时也被称为多分类器系统
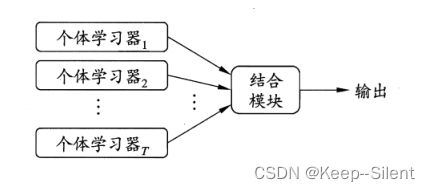
如在二分类中,采用个体学习器少数服从多数原则,进行预测

个体学习器应满足“好而不同”:
- 个体学习器不同:避免集成不起作用
- 个体学习器有一定的准确率:避免集成起副作用
7.2Boosting和AdaBoost
Boosting是一族可将弱学习器提升为强学习器的算法.这族算法的工作机制类似:先从初始训练集训练出一个基学习器,再根据基学习器的表现对训练样本分布进行调整,使得先前基学习器做错的训练样本在后续受到更多关注,然后基于调整后的样本分布来训练下一个基学习器;如此重复进行,直至基学习器数目达到事先指定的值T,最终将这T个基学习器进行加权结合.其中最著名的代表是AdaBoost
AdaBoost是基于“加性模型”,即基学习器的线性组合 H ( x ) = ∑ t = 1 T α t h t ( x ) H(\boldsymbol{x})= \sum_{t=1}^{T} \alpha_{t}h_{t} (\boldsymbol{x}) H(x)=t=1∑Tαtht(x)
7.3Bagging和随机森林
为获得好的集成,我们同时还希望个体学习器不能太差.如果采样出的每个子集都完全不同*,则每个基学习器只用到了一小部分训练数据,甚至不足以进行有效学习,这显然无法确保产生出比较好的基学习器.为解决这个问题,我们可考虑使用相互有交叠的采样子集.
7.3.1Bagging
简单来说,我们可采样出T个含m个训练样本的采样集,然后基于每个采样集训练出一个基学习器,再将这些基学习器进行结合.这就是Bagging 的基本流程.
在对预测输出进行结合时,Bagging 通常对分类任务使用简单投票法,对回归任务使用简单平均法.若分类预测时出现两个类收到同样票数的情形,则最简单的做法是随机选择一个,也可进一步考察学习器投票的置信度来确定最终胜者
自助采样过程还给Bagging带来了另一个优点:由于每个基学习器只使用了初始训练集中约63.2%的样本,剩下约36.8%的样本可用作验证集来对泛化性能进行“包外估计” 为此需记录每个基学习器所使用的训练样本.令 D t D_t Dt:表示 h t h_t ht实际使用的训练样本集,令 H o o b ( x ) H^{oob}(x) Hoob(x)表示对样本 x x x的包外预测,即(仅考虑那些未使用 x x x训练的基学习器在 x x x上的预测,有 H o o b ( x ) = arg max y ∈ Y ∑ t = 1 T I ( h t ( x ) = y ) ⋅ I ( x ∉ D t ) H^{\boldsymbol{oob}}(\boldsymbol{x})= \arg\max_{y\in\mathcal{Y}} \sum_{t=1}^T\mathbb{I}(h_t(\boldsymbol{x})=y) \cdot\mathbb{I}(\boldsymbol{x}\notin D_t) Hoob(x)=argy∈Ymaxt=1∑TI(ht(x)=y)⋅I(x∈/Dt)
则Bagging泛化误差的包外估计为 ϵ o o b = 1 ∣ D ∣ ∑ ( x , y ) ∈ D I ( H o o b ( x ) ≠ y ) \epsilon^{oob}= \frac1{|D|} \sum_{(\boldsymbol{x},y)\in D} \mathbb{I}(H^{oob} (\boldsymbol{x})\neq y) ϵoob=∣D∣1(x,y)∈D∑I(Hoob(x)=y)
7.3.2随机森林
随机森林(Random Forest,简称RF)是 Bagging 的一个扩展变体.RF在以决策树为基学习器构建Bagging集成的基础上,进一步在决策树的训练过程中引入了随机属性选择.具体来说,传统决策树在选择划分属性时是在当前结点的属性集合(假定有d个属性)中选择一个最优属性;而在RF中,对基决策树的每个结点,先从该结点的属性集合中随机选择一个包含k个属性的子集,然后再从这个子集中选择一个最优属性用于划分.这里的参数k控制了随机性的引入程度:若令k = d,则基决策树的构建与传统决策树相同;若令k= 1,则是随机选择一个属性用于划分;一般情况下,推荐值 k = log 2 d k = \log_2 d k=log2d
7.4结合策略
7.4.1平均法
简单平均法: H ( x ) = 1 T ∑ i = 1 T h i ( x ) H(\boldsymbol{x})=\frac1T\sum_{i=1}^Th_i(\boldsymbol{x}) H(x)=T1i=1∑Thi(x)
加权平均法: H ( x ) = ∑ i = 1 T w i h i ( x ) ( w i ⩾ 0 , ∑ i = 1 T w i = 1 ) H(\boldsymbol{x})=\sum_{i=1}^Tw_ih_i(\boldsymbol{x}) \;(w_i\geqslant0,\sum_{i=1}^Tw_i=1) H(x)=i=1∑Twihi(x)(wi⩾0,i=1∑Twi=1)
加权平均法的权重一般是从训练数据中学习而得,现实任务中的训练样本通常不充分或存在噪声,这将使得学出的权重不完全可靠.加权学习法不一定优于简单平均法。
7.4.2投票法
对分类任务来说,学习器h将从类别标记集合 { c 1 , c 2 , . . . , c N } \{c_1,c_2,...,c_N\} {c1,c2,...,cN}中预测出一个标记,最常见的结合策略是使用投票法.为便于讨论,我们将 h i h_i hi在样本 x x x上的预测输出表示为一个N维向量 ( h i 1 ( x ) ; h i 2 ( x ) ; … ; h i m ( x ) ) (h_i^1(\boldsymbol{x}); h_i^2(\boldsymbol{x}); \ldots; h_i^m(\boldsymbol{x})) (hi1(x);hi2(x);…;him(x)),其中 h i h ( x ) h_i^h(x) hih(x)是 h i h_i hi在类别标记 c j c_j cj上的输出.
绝对多数投票法: H ( x ) = { c j , i f ∑ i = 1 T h i j ( x ) > 0.5 ∑ k = 1 m ∑ i = 1 T h i k ( x ) r e j e c t , o t h e r w i s e . H\left(\boldsymbol{x}\right)= \left\{\begin{array}{l}c_{j},&\displaystyle \mathrm{~if~}\sum_{i=1}^{T}h_{i}^{j} \left(\boldsymbol{x} \right)>0.5\sum_{k=1}^{m} \sum_{i=1}^{T}h_{i}^{k} \left(\boldsymbol{x}\right)\\ \mathrm{reject},& \mathrm{~otherwise}. \end{array}\right. H(x)=⎩ ⎨ ⎧cj,reject, if i=1∑Thij(x)>0.5k=1∑mi=1∑Thik(x) otherwise.
即若某标记得票过半数,则预测为该标记;否则拒绝预测.
相对多数投票法: H ( x ) = c arg max j ∑ i = 1 T h i j ( x ) H(\boldsymbol{x})=c_{\arg\max_j \sum_{i=1}^T h_i^j(\boldsymbol{x})} H(x)=cargmaxj∑i=1Thij(x)
即预测为得票最多的标记.
加权投票法: H ( x ) = c argmax j ∑ i = 1 T w i h i j ( x ) H(\boldsymbol{x})=c_{\underset{j}{\operatorname*{argmax}}\sum_{i=1}^Tw_ih_i^j(\boldsymbol{x})} H(x)=cjargmax∑i=1Twihij(x)
即加上了权重
7.4.3学习法
当训练数据很多时,一种更为强大的结合策略是使用“学习法”,即通过另一个学习器来进行结合.Stacking 是学习法的典型代表.这里我们把个体学习器称为初级学习器,用于结合的学习器称为次级学习器或元学习器.

7.6实验:Adaboost
先导入数据集,并显示部分数据
from numpy import *
import numpy as np
def loadDataSet(name):
dataMatrix = []; classLabels = []
fr = open(name)
for line in fr.readlines():
lineArr = line.strip().split()
dataMatrix.append(np.array([float(x) for x in lineArr[:-1]]))
classLabels.append(float(lineArr[-1]))
return np.array(dataMatrix), np.array(classLabels)
dataMatrix, classLabels=loadDataSet('07horseColicTraining.txt')
print(dataMatrix[:5])
print(classLabels[:5])
[[ 2. 1. 38.5 66. 28. 3. 3. 0. 2. 5. 4. 4. 0. 0. 0. 3. 5. 45. 8.4 0. 0. ]
[ 1. 1. 39.2 88. 20. 0. 0. 4. 1. 3. 4. 2. 0. 0. 0. 4. 2. 50. 85. 2. 2. ]
[ 2. 1. 38.3 40. 24. 1. 1. 3. 1. 3. 3. 1. 0. 0. 0. 1. 1. 33. 6.7 0. 0. ]
[ 1. 9. 39.1 164. 84. 4. 1. 6. 2. 2. 4. 4. 1. 2. 5. 3. 0. 48. 7.2 3. 5.3]
[ 2. 1. 37.3 104. 35. 0. 0. 6. 2. 0. 0. 0. 0. 0. 0. 0. 0. 74. 7.4 0. 0. ]]
[-1. -1. 1. -1. -1.]
stumpClassify是一个单层决策树,通过阈值比较分为两类:-1和1
- threshIneq是lt(less)时将小于等于阈值的数据分为-1,其余为1
- threshIneq是gt(greater)时将大于阈值的数据分为-1,其余为1
threshIneq姑且称为阈值划分方式
并测试这个函数
def stumpClassify(dataMatrix,attribute,threshVal,threshIneq):#just classify the data
retArray = ones((shape(dataMatrix)[0],1))
if threshIneq == 'lt':
retArray[dataMatrix[:,attribute] <= threshVal] = -1.0
else:
retArray[dataMatrix[:,attribute] > threshVal] = -1.0
return retArray
retArray=stumpClassify(dataMatrix,1,5,'lt')
print(retArray[:5])
retArray=stumpClassify(dataMatrix,1,5,'gt')
print(retArray[:5])
[[-1.]
[-1.]
[-1.]
[ 1.]
[-1.]]
[[ 1.]
[ 1.]
[ 1.]
[-1.]
[ 1.]]
buildStump将在属性、阈值、阈值划分方式三者中,找到一组误差最小的划分组合
buildStump将生成一个单层决策树,伪代码如下:
for 属性 in 所有属性:
for 阈值 in 最小到最大的step等分阈值:
for 阈值划分方式 in ['lt','gt']:
计算误差
如误差小于当前最小误差则更新
def buildStump(dataMatrix,classLabels,D):
n,m = shape(dataMatrix)
dataMatrix=mat(dataMatrix)
bestStump={}
minError=inf
step=10 #设置阈值个数
for attribute in range(m):
minValue=dataMatrix[:,attribute].min()
maxValue=dataMatrix[:,attribute].max()
stepSize=(maxValue-minValue)/step
for threshVal in np.arange(minValue-stepSize,maxValue+stepSize*2,stepSize):
for threshIneq in ['lt','gt']:
predictVal=stumpClassify(dataMatrix,attribute,threshVal,threshIneq)
predictVal=predictVal[:,0]
errArr = mat(ones((n,1)))
errArr[predictVal == classLabels] = 0
predictError = D.T*errArr
predictError=predictError[0,0]
# print("attribute %d, thresh %.2f, thresh ineqal: %s, the weighted error is %.3f" % (attribute, threshVal, threshIneq, predictError))
if predictError < minError:
minError = predictError
bestClasEst = predictVal.copy()
bestStump['attribute'] = attribute
bestStump['threshVal'] = threshVal
bestStump['threshIneq'] = threshIneq
bestStump['minError'] = minError
return bestStump,minError,bestClasEst
n,m = shape(dataMatrix)
D = mat(ones((n,1))/n)
bestStump,minError,bestClasEst=buildStump(dataMatrix,classLabels,D)
print(bestStump)
print('minError',minError)
{'attribute': 9, 'threshVal': 3.0, 'threshIneq': 'gt', 'minError': 0.28428093645484953}
minError,0.28428093645484953
完成核心代码adaBoostTrainDS,训练numIt个单层决策树
伪代码:
for i in range(numIt):
利⽤buildStump()函数找到最佳的单层决策树
将最佳单层决策树加⼊到单层决策树数组
计算alpha
计算新的权重向量D
更新累计类别估计值
def adaBoostTrainDS(dataArr,classLabels,numIt=10):
weakClassArr = []
m = shape(dataArr)[0]
D = mat(ones((n,1))/n) #init D to all equal
aggClassEst = mat(zeros((n,1)))
for i in range(numIt):
bestStump,error,classEst = buildStump(dataArr,classLabels,D)#build Stump
classEst=mat(classEst).T
alpha = float(0.5*log((1.0-error)/max(error,1e-16)))
bestStump['alpha'] = alpha
weakClassArr.append(bestStump)
expon = multiply(-1*alpha*mat(classLabels).T,classEst)
D = multiply(D,exp(expon))
D = D/D.sum()
aggClassEst += (alpha*classEst)
aggErrors = multiply(sign(aggClassEst) != mat(classLabels).T,ones((n,1)))
errorRate = aggErrors.sum()/n
if errorRate == 0.0: break
return weakClassArr
weakClassArr=adaBoostTrainDS(dataMatrix,classLabels)
for weakClass in weakClassArr:
print(weakClass)
{'attribute': 9, 'threshVal': 3.0, 'threshIneq': 'gt', 'minError': 0.28428093645484953, 'alpha': 0.4616623792657674}
{'attribute': 17, 'threshVal': 52.5, 'threshIneq': 'gt', 'minError': 0.3472332812161393, 'alpha': 0.3156114929327882}
{'attribute': 3, 'threshVal': 55.199999999999996, 'threshIneq': 'gt', 'minError': 0.35750587621595387, 'alpha': 0.29310293594973225}
{'attribute': 18, 'threshVal': 53.400000000000006, 'threshIneq': 'lt', 'minError': 0.3922730925346517, 'alpha': 0.2188836769233133}
{'attribute': 15, 'threshVal': 0.0, 'threshIneq': 'lt', 'minError': 0.4062170817974291, 'alpha': 0.18981304702807467}
{'attribute': 5, 'threshVal': 2.0000000000000004, 'threshIneq': 'gt', 'minError': 0.413744417033253, 'alpha': 0.17425370493717318}
{'attribute': 5, 'threshVal': 0.0, 'threshIneq': 'lt', 'minError': 0.43076646870832686, 'alpha': 0.13936233333702944}
{'attribute': 7, 'threshVal': 1.1999999999999997, 'threshIneq': 'gt', 'minError': 0.41936713025879085, 'alpha': 0.16268596062198426}
{'attribute': 4, 'threshVal': 28.799999999999997, 'threshIneq': 'lt', 'minError': 0.4346242541793776, 'alpha': 0.1315043363205097}
{'attribute': 12, 'threshVal': 1.2, 'threshIneq': 'lt', 'minError': 0.44328851139912123, 'alpha': 0.11391315330833288}
经过adaBoostTrainDS算法,可训练出多个个体学习器weakClassArr(如上,训练了十个个体学习器)
为了进行评判学习器:
- 完成adaClassify函数(用weakClassArr进行预测)
- 完成adaAcc函数:得到某数据集的预测准确度
def adaClassify(datToClass,classifierArr):
dataMatrix = mat(datToClass)
n,m = shape(dataMatrix)
aggClassEst = mat(zeros((n,1)))
for i in range(len(classifierArr)):
classEst = stumpClassify(dataMatrix, classifierArr[i]['attribute'],\
classifierArr[i]['threshVal'],\
classifierArr[i]['threshIneq'])#call stump classify
aggClassEst += classifierArr[i]['alpha']*classEst
return sign(aggClassEst)
aggClassEst=adaClassify(dataMatrix,weakClassArr)
def adaAcc(dataMatrix,classLabels,weakClassArr):
n,m = shape(dataMatrix)
predict=adaClassify(dataMatrix,weakClassArr)
accArr=[(1 if predict[i,0]==classLabels[i] else 0) for i in range(n)]
return sum(accArr)/n
acc=adaAcc(dataMatrix,classLabels,weakClassArr)
print(acc)
0.7591973244147158
先分别导入训练集和测试集
再用训练集分别训练出含有不同个数的集成学习器
最后用数据集进行对这些集成学习器进行测试
trainData,trainLabel=loadDataSet('07horseColicTraining.txt')
testData,testLabel=loadDataSet('07horseColicTest.txt')
classNumbers=[1,10,30,50,100,500]
print('|classNumber|train Acc|test Acc|')
print('|--|--|--|')
for classNumber in classNumbers:
weakClassArr=adaBoostTrainDS(dataMatrix,classLabels,classNumber)
trainAcc=adaAcc(trainData,trainLabel,weakClassArr)
testAcc=adaAcc(testData,testLabel,weakClassArr)
print('|%d|%.2f%%|%.2f%%|'%(classNumber,trainAcc*100,testAcc*100))
| classNumber | train Acc | test Acc |
|---|---|---|
| 1 | 71.57% | 73.13% |
| 10 | 75.92% | 76.12% |
| 30 | 78.93% | 77.61% |
| 50 | 79.93% | 79.10% |
| 100 | 82.27% | 77.61% |
| 500 | 84.62% | 76.12% |
通过此表格可以看出,当基学习器少的时候,随着学习器个数的增加,对于训练数据和测试数据,集成学习器的预测准确度都不断提高。
当基学习器过多的时候,集成学习器对训练数据的预测准确度仍在提高,但是对测试数据的预测准确度不断降低,即出现了过拟合的情形。
结论:
- 多个个体学习器结合形成的集成学习器确实比一个学习器更优
- 学习器数量的选择不应过少或过多。过少则还有提升空间,过多则会过拟合


